-

The Feminist Botanist
A 19th-century tale of hermaphrodite flowers, Charles Darwin, and women’s right to vote.
-

The Shark Whisperer
Donald Nelson spent his life undoing the damage that Jaws did to the perception of sharks.
-

Nine Rebel Astronomy Theories That Went Dark
Bright ideas from astronomy’s biggest stars haven’t always worked out.
The Porthole
Short sharp looks at science
-

What a Bronze Age Skeleton Reveals About Cavities
Here’s a hint: He didn’t eat processed foods and sugar.
-

Archaeology at the Bottom of the Sea
David Gibbins on his 3 greatest revelations while writing A History of the World in Twelve Shipwrecks.
Get the best of Nautilus. Become a member today.
Join now-

The Marvelous Seamounts of the Southeast Pacific
An expedition to a little-explored region returns with deep-sea wonders.
-

The Ocean Apocalypse Is Upon Us, Maybe
What we know—and don’t know—about a crucial climate tipping point.
-

The Women Who Found Liberation in Seaweed
How a shared love of algae got a community of women hooked on marine science.
-

The Invasive Species
When it comes to tinkering with nature, our résumé is a list of breathtaking mistakes.
-

He Closed the Gap Between Humans and Apes
Frans de Waal saw animal behavior with fresh eyes and forever enriched our understanding of primates.
-

The End of the Dark Universe?
A new “post-quantum” theory of gravity says we can wave dark matter and dark energy goodbye.
-

Does Science Fiction Shape the Future?
Conversations with visionary science fiction authors on the social impact of their work.
-

Do Our Oceans Feel the Tug of Mars?
Ancient currents seemed to move in concert with a 2.4 million-year dance between the Red Planet and Earth.
-

Let’s Get Granular
Scientists have long puzzled over the behavior of mixed particles in rivers and landslides. New clues could be groundbreaking.
-

When Calamity Comes at a Crawl
Climate change may exacerbate the quiet catastrophe of slow-moving landslides.
-
The Part-Time Climate Scientist
A humble steam engineer put humans in the driver’s seat. -
A Revolution in Time
Why clocks need to follow the tempo of nature. -
Lithium, the Elemental Rebel
What a missing element can teach us about the universe. -
The Marine Biologist Who Dove Right In
He changed the study of ocean life by getting in the water. -
The Rebel Issue
How we change the world. -
The Prizefighters
If you want to know what it takes to succeed in science, head to the Nobel Prize ceremony. -
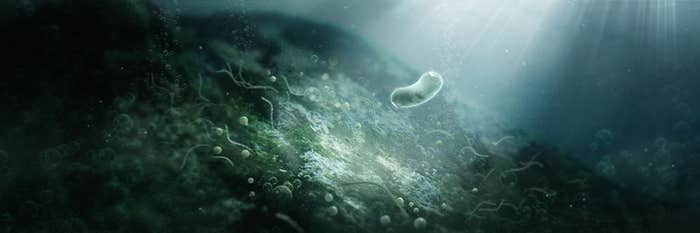
The Bacteria That Revolutionized the World
How cyanobacteria killed one climate and created our habitable Earth. -
How a Total Eclipse Alters Your Psyche
The importance of feeling small and insignificant. -
Doubts Grow About the Biosignature Approach to Alien-Hunting
Recent controversies bode ill for the effort to detect life on other planets by analyzing the gases in their atmospheres. -
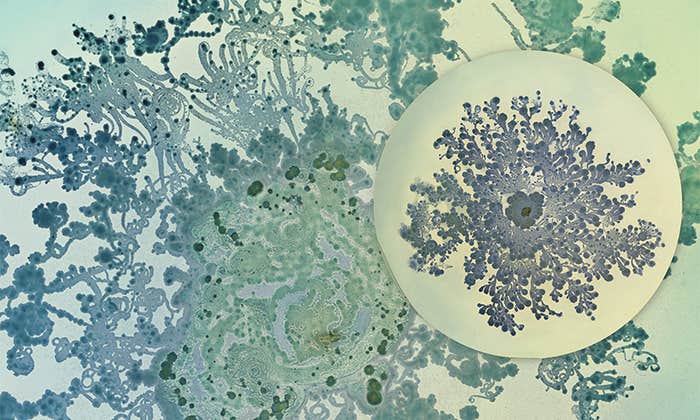
When Bacteria Are Beautiful
Making art out of an invisible world that shapes human health and disease. -
How Much Carbon Can a Tree Really Store?
A new study says climate change is messing with the math. -
When Sleep Deprivation Is an Antidepressant
For some, a night without sleep causes mood-boosting changes in the brain. -
How Different Instruments Shape the Music We Love
The timbre of a violin or a sitar can affect how dissonant music sounds to us. -
The Unseen Deep-Sea Legacy of Whaling
It’s not just whales who were decimated, but the creatures who live where they fall. -
Everything in Its Right Place
When a misplaced sense of familiarity gives rise to delusions of place. -
Scientists and Artists as Storytelling Teams
A conversation with artist and naturalist Zoe Keller. -
These Eyes Shine Light on the Path of Evolution
The visual systems of a group of mollusks reveal how future evolution depends on the past. -
Why Bats Are Flying Machines
Nearly everything about this tiny mammal is shaped by its powers of flight. -
The Plight of Japan’s Ama Divers
Practiced mostly by women, this fishing tradition is thousands of years old. Can it survive?