Despite the man’s awkward gestures, unkempt hair, and ill-fitting suit, it was one of the most extraordinary speeches that Reverend John Gulliver had ever heard. It was March 1860, and the venue was Norwich, Connecticut. The following morning Gulliver struck up conversation with the speaker, a politician by the name of Abraham Lincoln, as he caught a train down to Bridgeport.
As the pair took their seats in the carriage, Gulliver asked Lincoln about his remarkable oratory skill: “I want very much to know how you got this unusual power of ‘putting things.’ ” According to Gulliver, Lincoln said it wasn’t a matter of formal education. “I never went to school more than six months in my life.” But he did find training elsewhere. “In the course of my law-reading I constantly came upon the word demonstrate,” Lincoln said. “I thought, at first, that I understood its meaning, but soon became satisfied that I did not.” Resolving to understand it better, he went to his father’s house and “staid there till I could give any propositions in the six books of Euclid at sight.”1
He was referring to the first six of books of Euclid’s Elements, an Ancient Greek mathematical text. On the face of it, Euclid’s Elements was nothing but a dry textbook: There were no illustrative examples, no mention of people, and no motivation for the analyses it presented. But it was also a landmark, a way of constructing universal truths, a wonder that would outlast even the great lighthouse in Euclid’s home city of Alexandria.
Elements proposed that definitions were at the foundation of knowledge, and led to self-evident axioms that needed no proof. From these definitions and axioms, Euclid showed how to prove dozens of mathematical propositions, producing knowledge that was objective and undeniable. A person of reason would have to accept a proven fact, no matter what their personal beliefs or convictions were.
Elements would become a best-selling work, second only to the bible in printed editions, and used until recently as the standard text for mathematics classes. It profoundly influenced Western thought, and shaped Western science and art. What’s less recognized is its role in the creation of modern politics: The distance from proofs about equilateral triangles to the foundations of democracy in Europe and the United States turned out to be just about two millennia.
John Locke was an early pioneer of Euclidean thinking in politics. Born in 1632, the Englishman grew up in a time of turbulence, with a nine-year civil war beginning in 1642. Locke, whose father had fought against the Royalists in the war, would go on to develop a great interest in the concept of morality. In forming his ideology, Locke took guidance from the logical structure of Elements. He believed that by following the logical consequences of self-evident statements “as incontestable as those in mathematics,” it would be possible to demonstrate what was right and wrong.
Historically, absolute monarchs and the church had dictated laws and justice. Enlightenment thinkers such as Locke sought to challenge this tradition. Rather than defining equality from above, he wanted to root it in natural, objective laws. Locke believed that the “natural rights” of a society could be established in a similar manner to geometric theorems, and would therefore be “as certain as any demonstration of Euclid.”
Like Euclid, Locke defined terms, then used these definitions to prove moral claims. For example, Locke defined property as “a right to any thing,” and injustice as “the invasion or violation of that right.” The statement “where there is no property there is no injustice” resulted naturally from these definitions. In his Two Treatises of Government, published in 1689, Locke noted that “creatures of the same species and rank, promiscuously born to all the same advantages of nature, and the use of the same faculties, should also be equal one amongst another.” It was therefore self-evident that, in the absence of rules or laws, humanity’s natural state was “free, equal, and independent.” He concluded that the aim of a government should be to preserve the natural rights of life, liberty, and property.
Locke’s thinking would flow across the Atlantic, into the pens of the American Founding Fathers. The final version of the United States Declaration of Independence, drafted by Thomas Jefferson in 1776, opens with “We hold these truths to be self-evident, that all men are created equal.” A keen student of mathematics himself, Jefferson had adopted Euclid and Locke’s logical style, from the “self-evident” nature of the truths to the subsequent right to “life, liberty, and the pursuit of happiness.”
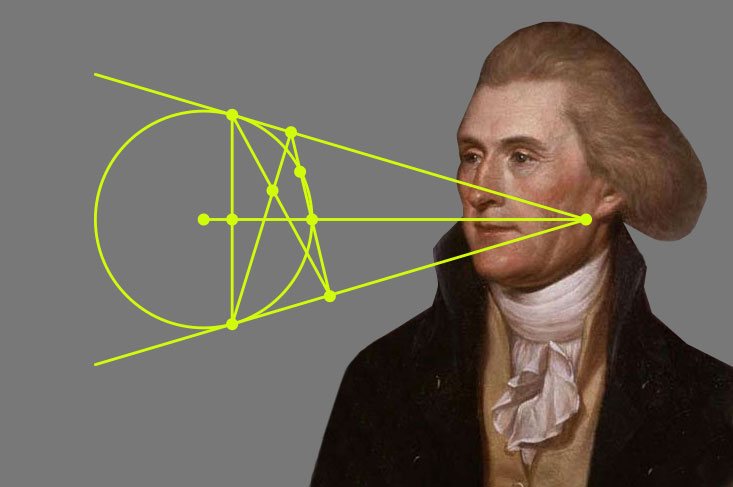
Nearly a century later, Lincoln had found his own way to Euclid. While working as a lawyer on the Illinois circuit during the early 1850s, he carried Euclid’s texts in his saddlebag. One time, his colleague William Herndon entered their shared office in Springfield to find Lincoln was surveying a vast canvas of diagrams. Lincoln was so taken with the shapes on the thick paper sheets that he barely acknowledged Herndon as he walked in. Bottles of ink lay scattered on the table, alongside pencils, a compass, a ruler, and a large pile of fresh paper—the results of a fruitless effort to “square the circle,” a classic Euclidean puzzle which involves drawing a square and a circle of equal area.
While Lincoln had to admit defeat after three days of drawing and measuring, Euclid’s mathematical principles and system of logic would go on to become a crucial tool throughout his political career. Euclidean logic would shape his arguments against slavery, and his debates against its proponents. It would convince him of what was just, and what was unacceptable. As he rose to the presidency, and as the nation descended into civil war, Euclid would be there to guide him.
A person of reason would have to accept a proven fact, no matter what their personal beliefs or convictions were.
“If A can prove, however conclusively, that he may, of right, enslave B,” Lincoln conjectured in a private 1854 essay, “why may not B snatch the same argument, and prove equally, that he may enslave A?” The argument was clear and irrefutable: Regardless of whether the right to own slaves was defined by color, intellect, or money, an enslaver could always use the same reasoning to enslave their supposed superior.
It was a textbook example of a kind of proof often used in mathematics, called proof by contradiction. In Elements, Euclid used this proof method to show that if two angles in a triangle are equal, the sides opposite them will be equal too. First, he assumed that one side was longer than the other. If he cut off the excess, however, so both sides were the same length, the smaller triangle would be in every way identical to the original. This contradicted his axiom that “the whole is greater than the part.” Hence both sides must always be equal. Lincoln’s proof had followed this same structure.
Lincoln’s main rival on the Illinois political circuit was Democrat Judge Stephen Douglas, who did not share Lincoln’s opposition to slavery. When the Founding Fathers talked of equality, Douglas claimed in 1857, they were not really referring to all men, “they were speaking of British subjects on this continent being equal to British subjects born and residing in Great Britain.” Lincoln countered by once again following the logic to its absurd conclusion. If the Declaration only referred British subjects, Lincoln argued, “the French, Germans, and other white people of the world are all gone to pot along with the Judge’s inferior races.”

During 1858, Lincoln and Douglas—who were running against each other for the Senate—engaged in a series of debates. Once again, Lincoln turned to Euclid. When Douglas criticized a legal point made by Senator Lyman Trumbull by calling him dishonest, Lincoln told Douglas that logical arguments could not be defeated with personal insults. “If you have ever studied geometry, you remember that by a course of reasoning, Euclid proves that all the angles in a triangle are equal to two right angles,” Lincoln said. “Euclid has shown you how to work it out. Now, if you undertake to disprove that proposition, and to show that it is erroneous, would you prove it to be false by calling Euclid a liar?”
Douglas argued that slavery was a sovereign right, to be decided by the people of each state. Lincoln disagreed: The notion of popular sovereignty should not include slavery. The following year, Lincoln challenged Douglas to construct a logically sound argument to support his case. “If Judge Douglas will demonstrate somehow that this is popular sovereignty—the right of one man to make a slave of another, without any right in that other, or anyone else to object—demonstrate it as Euclid demonstrated propositions, there is no objection.”
Euclid would have been proud.
As powerful as they were, there was also a limit to using Euclid’s axioms to argue the issues of the day. Euclidean logic relied on the concept of common axioms, agreed upon by all. But what if there wasn’t general agreement on those axioms? Progress could be difficult to come by. Speaking once in the city of Peoria, Illinois in October 1854, Lincoln became frustrated with Douglas’ view that Illinois was not founded as a free state. “To deny these things is to deny our national axioms,” Lincoln said. Which, in his view, made argument hopeless. “If a man will stand up and assert, and repeat, and re-assert, that two and two do not make four, I know nothing in the power of argument that can stop him.” By the end of the 1850s, when slavery had drawn a dividing line through the United States, Lincoln would write “One would start with great confidence that he could convince any sane child that the simpler propositions of Euclid are true, but, nevertheless, he would fail, utterly, with one who should deny the definitions and axioms. The principles of Jefferson are the definitions and axioms of free society. And yet they are denied and evaded, with no small show of success.”
Not only did Lincoln begin to reach the limits of axiomatic persuasion, the very idea of a fixed set of Euclidian axioms began to dissolve during this period, even in its native field of mathematics. In the 19th century mathematicians revisited classical questions in Euclidean geometry, such as whether it was possible to square the circle as Lincoln had attempted (it wasn’t). Others challenged the nature of geometry itself. Researchers like Carl Gauss explored non-Euclidean realms, in which Euclid’s theorems no longer held: Draw a triangle on the surface of a sphere, and its three angles no longer add up to two right angles.
“Would you prove it to be false by calling Euclid a liar?”
By the end of the century, mathematicians such as Georg Cantor were going further, and finding paradoxes and inconsistencies at the very heart of pure mathematics. Their predecessors had developed theorems based on the “intuitively evident” laws of nature, such as Euclid’s axiom that “the whole is greater than the part.” Real life intuition suggests this statement is always true, but Cantor found that it failed when applied to infinite collections of numbers. For example, Cantor demonstrated that the set of positive integers (1, 2, 3 …) had an equivalent “size” to the set of square numbers (1, 4, 9 …). The whole, in other words, was not always larger than the part.
In the early 20th century, researchers tried to tackle the growing number of paradoxes by building a set of complete, consistent axioms, from which all mathematical theories could be derived. Unfortunately, Kurt Gödel’s 1931 incompleteness theorems showed this aim to be impossible. He proved that no matter how detailed the axioms, there were always some situations that they would not cover. Gödel’s work demonstrated the limitations of axiomatic systems: Mathematics could not be both complete and consistent. Axioms were simply not enough.
So how could they be for politics? Abolishing slavery eventually required a new rule—the Thirteenth Amendment—implicitly implying that slavery was not so self-evidently prohibited by the constitution as it stood. Other new interpretations of American national axioms also made themselves felt. In 1896, the U.S. Supreme Court had ruled that “separate but equal” facilities for different races did not contradict the constitution. But attitudes gradually changed, and in 1954 they reversed the decision, noting that “separate educational facilities are inherently unequal.” Denial of women’s suffrage in the early 20th century and internment of Japanese Americans during World War II—both deemed constitutional at the time but subsequently condemned—further illustrate the shifting the notion of equality.
All of this amendment and re-evaluation mirrored Lincoln’s realization that we cannot rely on untouchable and self-evident truths. In his 1863 Gettysburg Address, he described the U.S. as a nation “dedicated to the proposition that all men are created equal.” The axiomatic project had to give way to a more modern project of ongoing interpretation—of propositions—whether it was in math or in politics. Barack Obama put it this way in a speech last year, following a U.S. Supreme Court ruling that same-sex marriage was a constitutional right. “Our nation was founded on a bedrock principle that we are all created equal. The project of each generation is to bridge the meaning of those founding words with the realities of changing times.” Equality, over time, has changed from a self-evident conclusion to a proposition. The proof of that proposition, Lincoln hoped, would be the United States itself.
Adam Kucharski is an assistant professor at the London School of Hygiene & Tropical Medicine, and the author of The Perfect Bet: How Science and Math Are Taking the Luck Out of Gambling.
References
1. Carpenter, F.B. The Inner Life of Abraham Lincoln: Six Months at the White House Hurd & Houghton, New York, NY (1874).



























