With his marriage to Norma Levor over, Claude Shannon was a bachelor again, with no attachments, a small Greenwich Village apartment, and a demanding job. His evenings were mostly his own, and if there’s a moment in Shannon’s life when he was at his most freewheeling, this was it. He kept odd hours, played music too loud, and relished the New York jazz scene. He went out late for raucous dinners and dropped by the chess clubs in Washington Square Park. He rode the A train up to Harlem to dance the jitterbug and take in shows at the Apollo. He went swimming at a pool in the Village and played tennis at the courts along the Hudson River’s edge. Once, he tripped over the tennis net, fell hard, and had to be stitched up.
His home, on the third floor of 51 West Eleventh Street, was a small New York studio. “There was a bedroom on the way to the bathroom. It was old. It was a boardinghouse … it was quite romantic,” recalled Maria Moulton, the downstairs neighbor. Perhaps somewhat predictably, Shannon’s space was a mess: dusty, disorganized, with the guts of a large music player he had taken apart strewn about on the center table. “In the winter it was cold, so he took an old piano he had and chopped it up and put it in the fireplace to get some heat.” His fridge was mostly empty, his record player and clarinet among the only prized possessions in the otherwise spartan space. Claude’s apartment faced the street. The same apartment building housed Claude Levi-Strauss, the great anthropologist. Later, Levi-Strauss would find that his work was influenced by the work of his former neighbor, though the two rarely interacted while under the same roof.
Though the building’s live-in super and housekeeper, Freddy, thought Shannon morose and a bit of a loner, Shannon did befriend and date his neighbor Maria. They met when the high volume of his music finally forced her to knock on his door; a friendship, and a romantic relationship, blossomed from her complaint.

Maria encouraged him to dress up and hit the town. “Now this is good!” he would exclaim when a familiar tune hit the radio on their drives. He read to her from James Joyce and T.S. Eliot, the latter his favorite author. He was, she remembered, preoccupied with the math problems he worked over in the evenings, and he was prone to writing down stray equations on napkins at restaurants in the middle of meals. He had few strong opinions about the war or politics, but many about this or that jazz musician. “He would find these common denominators between the musicians he liked and the ones I liked,” she remembered. He had become interested in William Sheldon’s theories about body types and their accompanying personalities, and he looked to Sheldon to understand his own rail-thin (in Sheldon’s term, ectomorphic) frame.
A few Bell Labs colleagues became Shannon’s closest friends. One was Barney Oliver. Tall, with an easy smile and manner, he enjoyed scotch and storytelling. Oliver’s easygoing nature concealed an intense intellect: “Barney was an intellect in the genius range, with a purported IQ of 180,” recalled one colleague. His interests spanned heaven and earth—literally. In time, he would become one of the leaders of the movement in the search for extraterrestrial life. Oliver also held the distinction of being one of the few to hear about Shannon’s ideas before they ever saw the light of day. As he proudly recalled later, “We became friends and so I was the mid-wife for a lot of his theories. He would bounce them off me, you know, and so I understood information theory before it was ever published.” That might have been a mild boast on Oliver’s part, but given the few people Shannon let into even the periphery of his thinking, it was notable that Shannon talked with him about work at all.
The answer to noise is not in how loudly we speak, but in how we say what we say.
John Pierce was another of the Bell Labs friends whose company Shannon shared in the off hours. At the Labs, Pierce “had developed a wide circle of devoted admirers, charmed by his wit and his lively mind.” He was Shannon’s mirror image in his thin figure and height—and in his tendency to become quickly bored of anything that didn’t intensely hold his interest. This extended to people. “It was quite common for Pierce to suddenly enter or leave a conversation or a meal halfway through,” wrote Jon Gertner.
Shannon and Pierce were intellectual sparring partners in the way only two intellects of their kind could be. They traded ideas, wrote papers together, and shared countless books over the course of their tenures at Bell Labs. Pierce told Shannon on numerous occasions that “he should write up this or that idea.” To which Shannon is said to have replied, with characteristic insouciance, “What does ‘should’ mean?”
Oliver, Pierce, and Shannon—a genius clique, each secure enough in his own intellect to find comfort in the company of the others. They shared a fascination with the emerging field of digital communication and co-wrote a key paper explaining its advantages in accuracy and reliability. One contemporary remembered this about the three Bell Labs wunderkinds:
It turns out that there were three certified geniuses at BTL [Bell Telephone Laboratories] at the same time, Claude Shannon of information theory fame, John Pierce, of communication satellite and traveling wave amplifier fame, and Barney. Apparently the three of those people were intellectually INSUFFERABLE. They were so bright and capable, and they cut an intellectual swath through that engineering community, that only a prestige lab like that could handle all three at once.
Other accounts suggest that Shannon might not have been so “insufferable” as he was impatient. His colleagues remembered him as friendly but removed. To Maria, he confessed a frustration with the more quotidian elements of life at the Labs. “I think it made him sick,” she said. “I really do. That he had to do all that work while he was so interested in pursuing his own thing.”
Partly, it seems, the distance between Shannon and his colleagues was a matter of sheer processing speed. In the words of Brockway McMillan, who occupied the office next door to Shannon’s, “he had a certain type of impatience with the type of mathematical argument that was fairly common. He addressed problems differently from the way most people did, and the way most of his colleagues did. … It was clear that a lot of his argumentation was, let’s say, faster than his colleagues could follow.” What others saw as reticence, McMillan saw as a kind of ambient frustration: “He didn’t have much patience with people who weren’t as smart as he was.”
It gave him the air of a man in a hurry, perhaps too much in a hurry to be collegial. He was “a very odd man in so many ways. … He was not an unfriendly person,” observed David Slepian, another Labs colleague. Shannon’s response to colleagues who could not keep pace was simply to forget about them. “He never argued his ideas. If people didn’t believe in them, he ignored those people,” McMillan told Gertner.
George Henry Lewes once observed that “genius is rarely able to give an account of its own processes.” This seems to have been true of Shannon, who could neither explain himself to others, nor cared to. In his work life, he preferred solitude and kept his professional associations to a minimum. “He was terribly, terribly secretive,” remembered Moulton. Robert Fano, a later collaborator of Shannon, said, “he was not someone who would listen to other people about what to work on.” One mark of this, some observed, was how few of Shannon’s papers were coauthored.
Shannon wouldn’t have been the first genius with an inward-looking temperament, but even among the brains of Bell Labs, he was a man apart. “He wouldn’t have been in any other department successfully. … You would knock on the door and he would talk to you, but otherwise, he kept to himself,” McMillan said.
There was something else, too, something that might have kept him at a remove from even his close colleagues: Shannon was moonlighting. On the evenings he was at home, Shannon was at work on a private project. It had begun to crystallize in his mind in his graduate school days. He would, at various points, suggest different dates of provenance. But whatever the date on which the idea first implanted itself in his mind, pen hadn’t met paper in earnest until New York and 1941. Now this noodling was both a welcome distraction from work at Bell Labs and an outlet to the deep theoretical work he prized so much, and which the war threatened to foreclose. Reflecting on this time later, he remembered the flashes of intuition. The work wasn’t linear; ideas came when they came. “These things sometimes … one night I remember I woke up in the middle of the night and I had an idea and I stayed up all night working on that.”
To picture Shannon during this time is to see a thin man tapping a pencil against his knee at absurd hours. This isn’t a man on a deadline; it’s something more like a man obsessed with a private puzzle, one that is years in the cracking. “He would go quiet, very very quiet. But he didn’t stop working on his napkins,” said Maria. “Two or three days in a row. And then he would look up, and he’d say, ‘Why are you so quiet?’ ”
Napkins decorate the table, strands of thought and stray sections of equations accumulate around him. He writes in neat script on lined paper, but the raw material is everywhere. Eight years like this— scribbling, refining, crossing out, staring into a thicket of equations, knowing that, at the end of all that effort, they may reveal nothing. There are breaks for music and cigarettes, and bleary-eyed walks to work in the morning, but mostly it’s this ceaseless drilling. Back to the desk, where he senses, perhaps, that he is on to something significant, something even more fundamental than the master’s thesis that made his name—but what?
Information was something guessed at rather than spoken of, something implied in a dozen ways before it was finally tied down. Information was a presence offstage. It was there in the studies of the physiologist Hermann von Helmholtz, who, electrifying frog muscles, first timed the speed of messages in animal nerves just as Thomson was timing the speed of messages in wires. It was there in the work of physicists like Rudolf Clausius and Ludwig Boltzmann, who were pioneering ways to quantify disorder—entropy—little suspecting that information might one day be quantified in the same way. Above all, information was in the networks that descended in part from the first attempt to bridge the Atlantic with underwater cables. In the attack on the practical engineering problems of connecting Points A and B—what is the smallest number of wires we need to string up to handle a day’s load of messages? how do we encrypt a top-secret telephone call?—the properties of information itself, in general, were gradually uncovered.
By the time of Claude Shannon’s childhood, the world’s communications networks were no longer passive wires acting as conduits for electricity, a kind of electron plumbing. They were continent-spanning machines, arguably the most complex machines in existence. Vacuum-tube amplifiers strung along the telephone lines added power to voice signals that would have otherwise attenuated and died out on their thousand-mile journeys. A year before Shannon was born, in fact, Bell and Watson inaugurated the transcontinental phone line by reenacting their first call, this time with Bell in New York and Watson in San Francisco. By the time Shannon was in elementary school, feedback systems managed the phone network’s amplifiers automatically, holding the voice signals stable and silencing the “howling” or “singing” noises that plagued early phone calls, even as the seasons turned and the weather changed around the sensitive wires that carried them. Each year that Shannon placed a call, he was less likely to speak to a human operator and more likely to have his call placed by machine, by one of the automated switchboards that Bell Labs grandly called a “mechanical brain.” In the process of assembling and refining these sprawling machines, Shannon’s generation of scientists came to understand information in much the same way that an earlier generation of scientists came to understand heat in the process of building steam engines.
The real measure of information is not in the symbols we send— it’s in the symbols we could have sent, but did not.
It was Shannon who made the final synthesis, who defined the concept of information and effectively solved the problem of noise. It was Shannon who was credited with gathering the threads into a new science. But he had important predecessors at Bell Labs, two engineers who had shaped his thinking since he discovered their work as an undergraduate at the University of Michigan, who were the first to consider how information might be put on a scientific footing, and whom Shannon’s landmark paper singled out as pioneers.
One was Harry Nyquist. Before Nyquist, engineers already understood that the electrical signals carrying messages through networks—whether telegraph, -phone, or -photo—fluctuated wildly up and down. Represented on paper, the signals would look like waves: not calmly undulating sine waves, but a chaotic, wind-lashed line seemingly driven without a pattern. Yet there was a pattern. Even the most anarchic fluctuation could be resolved into the sum of a multitude of calm, regular waves, all crashing on top of one another at their own frequencies until they frothed into chaos.
In this way, communications networks could carry a range, or a “band,” of frequencies. And it seemed that a greater range of frequencies imposed on top of one another, a greater “bandwidth,” was needed to generate the more interesting and complex waves that could carry richer information. To efficiently carry a phone conversation, the Bell network needed frequencies ranging from about 200 to 3,200 hertz, or a bandwidth of 3,000 hertz. Telegraphy required less; television would require 2,000 times more.
Nyquist showed how the bandwidth of any communications channel provided a cap on the amount of “intelligence” that could pass through it at a given speed. But this limit on intelligence meant that distinction between continuous signals (like the message on a phone line) and discrete signals (like dots and dashes or, we might add, 0’s and 1’s) was much less clear-cut than it seemed. A continuous signal still varied smoothly in amplitude, but you could also represent that signal as a series of samples, or discrete time-slices—and within the limit of a given bandwidth, no one would be able to tell the difference. Practically, that result showed Bell Labs how to send telegraph and telephone signals on the same line without interference between the two. More fundamentally, as a professor of electrical engineering wrote, it showed that “the world of technical communications is essentially discrete or ‘digital.’ ”
In Nyquist’s words, “by the speed of transmission of intelligence is meant the number of characters, representing different letters, figures, etc., which can be transmitted in a given length of time.” This was much less clear than it might have been—but for the first time, someone was groping toward a meaningful way of treating messages scientifically. Here, then, is Nyquist’s formula for the speed at which a telegraph can send intelligence:
W=k log(m)
W is the speed of intelligence. m is the number of “current values” that the system can transmit. A current value is a discrete signal that a telegraph system is equipped to send: The number of current values is something like the number of possible letters in an alphabet. If the system can only communicate “on” or “off,” it has two current values; if it can communicate “negative current,” “off,” and “positive current,” it has three; and if it can communicate “strong negative,” “negative,” “off,” “positive,” and “strong positive,” it has five. Finally, k is the number of current values the system is able to send each second.
In other words, Nyquist showed that the speed at which a telegraph could transmit intelligence depended on two factors: the speed at which it could send signals, and the number of “letters” in its vocabulary. The more “letters” or current values that were possible, the fewer that would actually have to be sent over the wire.
Nyquist’s short digression on current values offered the first hint of a connection between intelligence and choice. But it remained just that. He was more interested in engineering more efficient systems than in speculating about the nature of this intelligence; and, more to the point, he was still expected to produce some measure of practical results. So, after recommending to his colleagues that they build more current values into their telegraph networks, he turned to other work. Nor, after leaving the tantalizing suggestion that all systems of communication resembled the telegraph in their digital nature, did he go on to generalize about communication itself. At the same time, his way of defining intelligence—“different letters, figures, etc.”—remained distressingly vague. Behind the letters and figures there was—what, exactly?
Reading the work of Ralph Hartley, Shannon said, was “an important influence on my life.” Not simply on his research or his studies: Shannon spent much of his life working with the conceptual tools that Hartley built, and for the better part of his life, much of his public identity—“Claude Shannon, Father of Information Theory”—was bound up in having been the one who extended Hartley’s ideas far beyond what Hartley, or anyone, could have imagined. In the 1939 letter in which Shannon first laid out the study of communications that he would complete nine years later, he used Nyquist’s “intelligence.” By the time the work was finished, he used Hartley’s crisper term: “information.” While an engineer like Shannon would not have needed the reminder, it was Hartley who made meaning’s irrelevance to information clearer than ever.
From the beginning, Hartley’s interests in communications networks were more promiscuous than Nyquist’s: He was in search of a single framework that could encompass the information-transmitting power of any medium—a way of comparing telegraph to radio to television on a common scale. And Hartley’s 1928 paper, which brought Nyquist’s work to a higher level of abstraction, came closer to the goal than anyone yet. Suiting that abstraction, the paper Hartley presented to a scientific conference at Lake Como, in Italy, was simply called “Transmission of Information.”
It was an august crowd that had assembled at the foot of the Alps for the conference. In attendance were Niels Bohr and Werner Heisenberg, two founders of quantum physics, and Enrico Fermi, who would go on to build the world’s first nuclear reactor, under the bleacher seats at the University of Chicago’s stadium—and Hartley was at pains to show that the study of information belonged in their company. He began by asking his audience to consider a thought experiment. Imagine a telegraph system with three current values: negative, off, and positive. Instead of allowing a trained operator to select the values with his telegraph key, we hook the key up to a random device, say, “a ball rolling into one of three pockets.” We roll the ball down the ramp, send a random signal, and repeat as many times as we’d like. We’ve sent a message. Is it meaningful?
Shannon took it for granted that meaning could be ignored.
It depends, Hartley answered, on what we mean by meaning. If the wire was sound and the signal undistorted, we’ve sent a clear and readable set of symbols to our receiver—much clearer, in fact, than a human-generated message over a faulty wire. But however clearly it comes through, the message is also probably gibberish: “The reason for this is that only a limited number of the possible sequences have been assigned meanings,” and a random choice of sequence is far more likely to be outside that limited range. There’s only meaning where there’s prior agreement about our symbols. And all communication is like this, from waves sent over electrical wires, to the letters agreed upon to symbolize words, to the words agreed upon to symbolize things.
For Hartley, these agreements on the meaning of symbol vocabularies all depend on “psychological factors”—and those were two dirty words. Some symbols were relatively fixed (Morse code, for instance), but the meaning of many others varied with language, personality, mood, tone of voice, time of day, and so much more. There was no precision there. If, following Nyquist, the quantity of information had something to do with choice from a number of symbols, then the first requirement was getting to clarity on the number of symbols, free from the whims of psychology. A science of information would have to make sense of the messages we call gibberish, as well as the messages we call meaningful. So in a crucial passage, Hartley explained how we might begin to think about information not psychologically, but physically: “In estimating the capacity of the physical system to transmit information we should ignore the question of interpretation, make each selection perfectly arbitrary, and base our results on the possibility of the receiver’s distinguishing the result of selecting any one symbol from that of selecting any other.”
The real measure of information is not in the symbols we send— it’s in the symbols we could have sent, but did not. To send a message is to make a selection from a pool of possible symbols, and “at each selection there are eliminated all of the other symbols which might have been chosen.” To choose is to kill off alternatives. Symbols from large vocabularies bear more information than symbols from small ones. Information measures freedom of choice.
In this way, Hartley’s thoughts on choice were a strong echo of Nyquist’s insight into current values. But what Nyquist demonstrated for telegraphy, Hartley proved true for any form of communication; Nyquist’s ideas turned out to be a subset of Hartley’s. In the bigger picture, for those discrete messages in which symbols are sent one at a time, only three variables controlled the quantity of information: the number k of symbols sent per second, the size s of the set of possible symbols, and the length n of the message. Given these quantities, and calling the amount of information transmitted H, we have:
H=k log sn
If we make random choices from a set of symbols, the number of possible messages increases exponentially as the length of our message grows. For instance, in our 26-letter alphabet there are 676 possible two-letter strings (or 262), but 17,576 three-letter strings (or 263). Hartley, like Nyquist before him, found this inconvenient. A measure of information would be more workable if it increased linearly with each additional symbol, rather than exploding exponentially. In this way, a 20-letter telegram could be said to hold twice as much information as a 10-letter telegram, provided that both messages used the same alphabet. That explains what the logarithm is doing in Hartley’s formula (and Nyquist’s): It’s converting an exponential change into a linear one. For Hartley, this was a matter of “practical engineering value.”
This, then, was roughly where information sat when Claude Shannon picked up the thread. What began in the 19th century as an awareness that we might speak to one another more accurately at a distance if we could somehow quantify our messages had— almost—ripened into a new science. Each step was a step into higher abstraction. Information was the electric flow through a wire. Information was a number of characters sent by a telegraph. Information was choice among symbols. At each iteration, the concrete was falling away.
As Shannon chewed all of this over for a decade in his bachelor’s apartment in the West Village or behind his closed door at Bell Labs, it seemed as if the science of information had nearly ground to a halt. Hartley himself was still on the job at Bell Labs, a scientist nearing retirement when Shannon signed on, but too far out of the mainstream for the two to collaborate effectively. The next and decisive step after Hartley could only be found with genius and time. We can say, from our hindsight, that if the step were obvious, it surely wouldn’t have stayed untaken for 20 years. If the step were obvious, it surely wouldn’t have been met with such astonishment.
“It came as a bomb,” said Pierce.
From the start, Shannon’s landmark paper, “A Mathematical Theory of Communication,” demonstrated that he had digested what was most incisive from the pioneers of information science. Where Nyquist used the vague concept of “intelligence” and Hartley struggled to explain the value of discarding the psychological and semantic, Shannon took it for granted that meaning could be ignored. In the same way, he readily accepted that information measures freedom of choice: What makes messages interesting is that they are “selected from a set of possible messages.” It would satisfy our intuitions, he agreed, if we stipulated that the amount of information on two punch cards doubled (rather than squared) the amount of information on one, or that two electronic channels could carry twice the information of one.
That was Shannon’s debt. What he did next demonstrated his ambition. Every system of communication—not just the ones existing in 1948, not just the ones made by human hands, but every system conceivable—could be reduced to a radically simple essence.
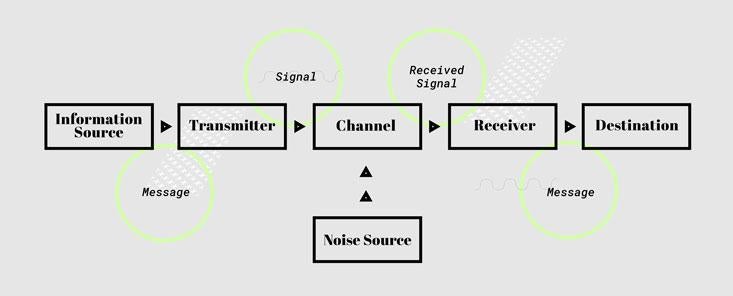
• The information source produces a message.
• The transmitter encodes the message into a form capable of being sent as a signal.
• The channel is the medium through which the signal passes.
• The noise source represents the distortions and corruptions that afflict the signal on its way to the receiver.
• The receiver decodes the message, reversing the action of the transmitter.
• The destination is the recipient of the message.
The beauty of this stripped-down model is that it applies universally. It is a story that messages cannot help but play out—human messages, messages in circuits, messages in the neurons, messages in the blood. You speak into a phone (source); the phone encodes the sound pressure of your voice into an electrical signal (transmitter); the signal passes into a wire (channel); a signal in a nearby wire interferes with it (noise); the signal is decoded back into sound (receiver); the sound reaches the ear at the other end (destination).
In one of your cells, a strand of your DNA contains the instructions to build a protein (source); the instructions are encoded in a strand of messenger RNA (transmitter); the messenger RNA carries the code to your cell’s sites of protein synthesis (channel); one of the “letters” in the RNA code is randomly switched in a “point mutation” (noise); each three-“letter” code is translated into an amino acid, protein’s building block (receiver); the amino acids are bound into a protein chain, and the DNA’s instructions have been carried out (destination).
Those six boxes are flexible enough to apply even to the messages the world had not yet conceived of—messages for which Shannon was, here, preparing the way. They encompass human voices as electromagnetic waves that bounce off satellites and the ceaseless digital churn of the Internet. They pertain just as well to the codes written into DNA. Although the molecule’s discovery was still five years in the future, Shannon was arguably the first to conceive of our genes as information bearers, an imaginative leap that erased the border between mechanical, electronic, and biological messages.
First, though, Shannon saw that information science had still failed to pin down something crucial about information: its probabilistic nature. When Nyquist and Hartley defined it as a choice from a set of symbols, they assumed that each choice from the set would be equally probable, and would be independent of all the symbols chosen previously. It’s true, Shannon countered, that some choices are like this. But only some. For instance, a fair coin has a 50-50 chance of landing heads or tails. This simplest choice possible—heads or tails, yes or no, 1 or zero—is the most basic message that can exist. It is the kind of message that actually conforms to Hartley’s way of thinking. It would be the baseline for the true measure of information.

New sciences demand new units of measurement—as if to prove that the concepts they have been talking and talking around have at last been captured by number. The new unit of Shannon’s science was to represent this basic situation of choice. Because it was a choice of 0 or 1, it was a “binary digit.” In one of the only pieces of collaboration Shannon allowed on the entire project, he put it to a lunchroom table of his Bell Labs colleagues to come up with a snappier name. Binit and bigit were weighed and rejected, but the winning proposal was laid down by John Tukey, a Princeton professor working at Bell. Bit.
One bit is the amount of information that results from a choice between two equally likely options. So “a device with two stable positions … can store one bit of information.” The bit-ness of such a device—a switch with two positions, a coin with two sides, a digit with two states—lies not in the outcome of the choice, but in the number of possible choices and the odds of the choosing. Two such devices would represent four total choices and would be said to store two bits. Because Shannon’s measure was logarithmic (to base 2—in other words, the “reverse” of raising 2 to the power of a given number), the number of bits doubled each time the number of choices offered was squared:

So think of the example at the opposite extreme: Think of a coin with two heads. Toss it as many times as you like—does it give you any information? Shannon insisted that it does not. It tells you nothing that you do not already know: It resolves no uncertainty.
What does information really measure? It measures the uncertainty we overcome. It measures our chances of learning something we haven’t yet learned. Or, more specifically: when one thing carries information about another—just as a meter reading tells us about a physical quantity, or a book tells us about a life—the amount of information it carries reflects the reduction in uncertainty about the object. The messages that resolve the greatest amount of uncertainty—that are picked from the widest range of symbols with the fairest odds—are the richest in information. But where there is perfect certainty, there is no information: There is nothing to be said.
Some choices are like this. But not all coins are fair.
“Do you swear to tell the truth, the whole truth, and nothing but the truth?” How many times in the history of courtroom oaths has the answer been anything other than “Yes”? Because only one answer is really conceivable, the answer provides us with almost no new information—we could have guessed it beforehand. That’s true of most human rituals, of all the occasions when our speech is prescribed and securely expected (“Do you take this man … ?”). And when we separate meaning from information, we find that some of our most meaningful utterances are also our least informative.
We might be tempted to fixate on the tiny number of instances in which the oath is denied or the bride is left at the altar. But in Shannon’s terms, the amount of information at stake lies not in one particular choice, but in the probability of learning something new with any given choice. A coin heavily weighted for heads will still occasionally come up tails—but because the coin is so predictable on average, it’s also information-poor.
Still, the most interesting cases lie between the two extremes of utter uncertainty and utter predictability: in the broad realm of weighted coins. Nearly every message sent and received in the real world is a weighted coin, and the amount of information at stake varies with the weighting. Here, Shannon showed the amount of information at stake in a coin flip in which the probability of a given side (call it p) varies from zero percent to 50 percent to 100 percent:
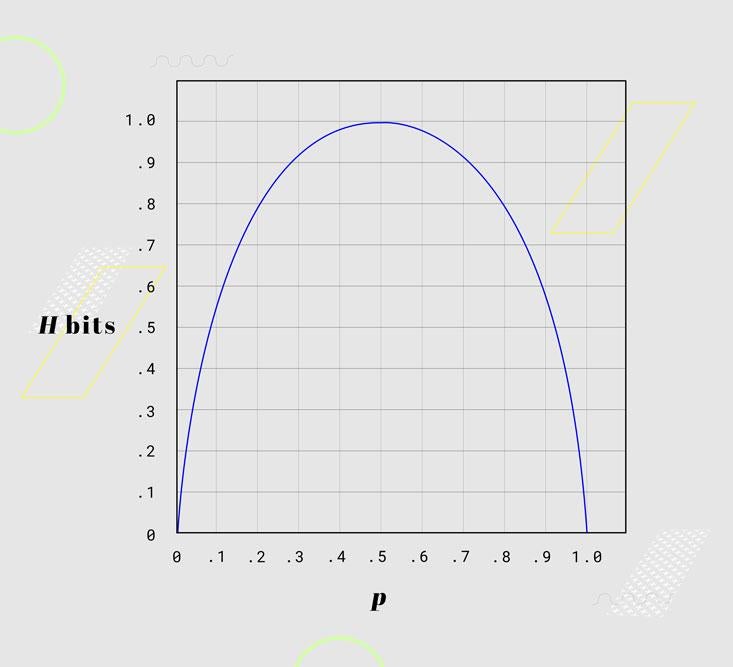
The case of 50-50 odds offers a maximum of one bit, but the amount of surprise falls off steadily as the choice grows more predictable in either direction, until we reach the perfectly predictable choice that tells us nothing. The special 50-50 case was still described by Hartley’s law. But now it was clear that Hartley’s theory was consumed by Shannon’s: Shannon’s worked for every set of odds. In the end, the real measure of information depended on those odds:
H = –p log p – q log q
Here, p and q are the probabilities of the two outcomes—of either face of the coin, or of either symbol that can be sent—which together add up to 100 percent. (When more than two symbols are possible, we can insert more probabilities into the equation.) The number of bits in a message (H) hangs on its uncertainty: The closer the odds are to equal, the more uncertain we are at the outset, and the more the result surprises us. And as we fall away from equality, the amount of uncertainty to be resolved falls with it. So think of H as a measure of the coin’s “average surprise.” Run the numbers for a coin weighted to come up heads 70 percent of the time and you find that flipping it conveys a message worth just about 0.9 bits.
Now, the goal of all this was not merely to grind out the precise number of bits in every conceivable message: In situations more complicated than a coin flip, the possibilities multiply and the precise odds of each become much harder to pin down. Shannon’s point was to force his colleagues to think about information in terms of probability and uncertainty. It was a break with the tradition of Nyquist and Hartley that helped to set the rest of Shannon’s project in motion—though, true to form, he dismissed it as trivial: “I don’t regard it as so difficult.”
Difficult or not, it was new, and it revealed new possibilities for transmitting information and conquering noise. We can turn unfair odds to our favor.
For the vast bulk of messages, in fact, symbols do not behave like fair coins. The symbol that is sent now depends, in important and predictable ways, on the symbol that was just sent. Because these rules render certain patterns more likely and certain patterns almost impossible, languages like English come well short of complete uncertainty and maximal information. From the perspective of the information theorist, our languages are hugely predictable—almost boring. And this predictability is the essential codebreaker’s tool, one with which Shannon was deeply familiar from his work as a cryptographer during World War II.
We can find a concrete example of the value of predictability for codebreaking in the story that was Shannon’s childhood favorite: Edgar Allan Poe’s “The Gold-Bug.” At the story’s climax, the eccentric treasure-hunter Mr. Legrand explains how he uncovered a pirate’s buried treasure by cracking this seemingly impenetrable block of code:
53‡‡†305))6*;4826)4‡.)4‡);806*;48†8’60))85;]8*:‡*8†83 (88)5*†;46(;88*96*?;8)*‡(;485);5*†2:*‡(;4956*2(5*-4)8’8*; 40 69285);)6†8)4‡‡;1(‡9;48081;8:8‡1;48†85;4)485†528806*81 (‡9;48;(88;4(‡?34;48)4‡;161;:188;‡?;
He began, as all good codebreakers did, by counting symbol frequencies. The symbol “8” occurred more than any other, 34 times. This small fact was the crack that brought the entire structure down. Here, in words that captivated Shannon as a boy, is how Mr. Legrand explained it:
Now, in English, the letter which most frequently occurs is e … .An individual sentence of any length is rarely seen, in which it is not the prevailing character. …
As our predominant character is 8, we will commence by assuming it as the e of the natural alphabet. …
Now, of all words in the language, “the” is the most usual; let us see, therefore, whether they are not repetitions of any three characters in the same order of collocation, the last of them being 8. If we discover repetitions of such letters, so arranged, they will most probably represent the word “the.” On inspection, we find no less than seven such arrangements, the characters being ;48. We may, therefore, assume that the semicolon represents t, that 4 represents h, and that 8 represents e—the last being now well confirmed. Thus a great step has been taken.
Being the work of a semiliterate pirate, the code was easy enough to break. More sophisticated ciphers would employ any number of stratagems to foil frequency counts: switching code alphabets partway through a message, eliminating double vowels and double consonants, simply doing without the letter “e.” The codes that Shannon helped develop during wartime were more convoluted still. But in the end, codebreaking remained possible, and remains so, because every message runs up against a basic reality of human communication. To communicate is to make oneself predictable.
The majority of what we say could just as well go unsaid.
This was the age-old codebreaker’s intuition that Shannon formalized in his work on information theory: Codebreaking works because our messages are less, much less, than fully uncertain. To be sure, it was not that Shannon’s work in cryptography drove his breakthrough in information theory: He began thinking about information years before he began thinking about codes in any formal sense—before, in fact, he knew that he’d be spending several years as a cryptographer in the service of the American government. At the same time, his work on information and his work on codes grew from a single source: his interest in the unexamined statistical nature of messages, and his intuition that a mastery of this nature might extend our powers of communication. As Shannon put it, it was all “information, at one time trying to conceal it, and at the other time trying to transmit it.”
In information theory’s terms, the feature of messages that makes code-cracking possible is redundancy. A historian of cryptography, David Kahn, explained it like this: “Roughly, redundancy means that more symbols are transmitted in a message than are actually needed to bear the information.” Information resolves our uncertainty; redundancy is every part of a message that tells us nothing new. Whenever we can guess what comes next, we’re in the presence of redundancy. Letters can be redundant: Because Q is followed almost automatically by U, the U tells us almost nothing in its own right. We can usually discard it, and many more letters besides. As Shannon put it, “MST PPL HV LTTL DFFCLTY N RDNG THS SNTNC.”
Words can be redundant: “the” is almost always a grammatical formality, and it can usually be erased with little cost to our understanding. Poe’s cryptographic pirate would have been wise to slash the redundancy of his message by cutting every instance of “the,” or “;48”—it was the very opening that Mr. Legrand exploited to such effect. Entire messages can be redundant: In all of those weighted-coin cases in which our answers are all but known in advance, we can speak and speak and say nothing new. On Shannon’s understanding of information, the redundant symbols are all of the ones we can do without—every letter, word, or line that we can strike with no damage to the information.
And if this redundancy grows out of the rules that check our freedom, it is also dictated by the practicalities of communicating with one another. Every human language is highly redundant. From the dispassionate perspective of the information theorist, the majority of what we say—whether out of convention, or grammar, or habit—could just as well go unsaid. In his theory of communication, Shannon guessed that the world’s wealth of English text could be cut in half with no loss of information: “When we write English, half of what we write is determined by the structure of the language and half is chosen freely.” Later on, his estimate of redundancy rose as high as 80 percent: Only one in five characters actually bear information.
As it is, Shannon suggested, we’re lucky that our redundancy isn’t any higher. If it were, there wouldn’t be any crossword puzzles. At zero redundancy, “any sequence of letters is a reasonable text in the language and any two dimensional array of letters forms a crossword puzzle.” At higher redundancies, fewer sequences are possible, and the number of potential intersections shrinks: if English were much more redundant, it would be nearly impossible to make puzzles. On the other hand, if English were a bit less redundant, Shannon speculated, we’d be filling in crossword puzzles in three dimensions.
Understanding redundancy, we can manipulate it deliberately, just as an earlier era’s engineers learned to play tricks with steam and heat. Of course, humans had been experimenting with redundancy in their trial-and-error way for centuries. We cut redundancy when we write shorthand, when we assign nicknames, when we invent jargon to compress a mass of meaning (“the left-hand side of the boat when you’re facing the front”) into a single point (“port”). We add redundancy when we say “V as in Victor” to make ourselves more clearly heard, when we circumlocute around the obvious, even when we repeat ourselves. But it was Shannon who showed the conceptual unity behind all of these actions and more. At the foundation of our Information Age—once wires and microchips have been stripped away, once the stream of 0’s and 1’s has been parted—we find Shannon’s two fundamental theorems of communication. Together they speak to the two ways in which we can manipulate redundancy: subtracting it, and adding it.
Every signal is subject to noise. Every message is liable to corruption, distortion, scrambling.
To begin with, how fast can we send a message? It depends, Shannon showed, on how much redundancy we can wring out of it. The most efficient message would actually resemble a string of random text: Each new symbol would be as informative as possible, and thus as surprising as possible. Not a single symbol would be wasted. So the speed with which we can communicate over a given channel depends on how we encode our messages: how we package them, as compactly as possible, for shipment. Shannon’s first theorem proves that there is a point of maximum compactness for every message source. We have reached the limits of communication when every symbol tells us something new.
And because we now have an exact measure of information, the bit, we also know how much a message can be compressed before it reaches that point of perfect singularity. It was one of the beauties of a physical idea of information, a bit to stand among meters and grams: proof that the efficiency of our communication depends not just on the qualities of our media of talking, on the thickness of a wire or the frequency range of a radio signal, but on something measurable, pin-downable, in the message itself. What remained, then, was the work of source coding: building reliable systems to wring the excess from our all-too-humanly redundant messages at the source, and to reconstitute them at the destination. Shannon, along with Massachusetts Institute of Technology engineer Robert Fano, made an important start in this direction.
Yet our messages also travel under threat. Every signal is subject to noise. Every message is liable to corruption, distortion, scrambling, and the most ambitious messages, the most complex pulses sent over the greatest distances, are the most easily distorted. Sometime soon—not in 1948, but within the lifetimes of Shannon and his Bell Labs colleagues—human communication was going to reach the limits of its ambition, unless noise could be solved.
That was the burden of Shannon’s second fundamental theorem. Unlike his first, which temporarily excised noise from the equation, the second presumed a realistically noisy world and showed us, within that world, the bounds of our accuracy and speed. Understanding those bounds demanded an investigation not simply of what we want to say, but of our means of saying it: the qualities of the channel over which our message is sent, whether that channel is a telegraph line or a fiber-optic cable.
Shannon’s paper was the first to define the idea of channel capacity, the number of bits per second that a channel can accurately handle. He proved a precise relationship between a channel’s capacity and two of its other qualities: bandwidth (or the range of frequencies it could accommodate) and its ratio of signal to noise. The groundbreaking fact about channel capacity, though, was not simply that it could be traded for or traded away. It was that there is a hard cap—a “speed limit” in bits per second—on accurate communication in any medium. Past this point, which was soon enough named the Shannon limit, our accuracy breaks down.
Shannon gave every subsequent generation of engineers a mark to aim for, as well as a way of knowing when they were wasting their time in pursuit of the hopeless. In a way, he also gave them what they had been after since the telegraph days of 19th century: an equation that brought message and medium under the same laws.
This would have been enough. But it was the next step that seemed, depending on one’s perspective, miraculous or inconceivable. Below the channel’s speed limit, we can make our messages as accurate as we desire—for all intents, we can make them perfectly accurate, perfectly free from noise. This was Shannon’s furthest-reaching find: the one Fano called “unknown, unthinkable,” until Shannon thought it.
Until Shannon, it was simply conventional wisdom that noise had to be endured. Shannon’s promise of perfect accuracy was something radically new. (In technical terms, it was a promise of an “arbitrarily small” rate of error: an error rate as low as we want, and want to pay for.) For engineering professor James Massey, it was this promise above all that made Shannon’s theory “Copernican”: Copernican in the sense that it productively stood the obvious on its head and revolutionized our understanding of the world. Just as the sun “obviously” orbited the earth, the best answer to noise “obviously” had to do with physical channels of communication, with their power and signal strength.
Shannon proposed an unsettling inversion. Ignore the physical channel and accept its limits: We can overcome noise by manipulating our messages. The answer to noise is not in how loudly we speak, but in how we say what we say.
In 1858, when the first attempted transatlantic telegraph cable broke down after just 28 days of service, the cable’s operators had attempted to cope with the faltering signal by repeating themselves. Their last messages across the Atlantic are a record of repetitions: “Repeat, please.” “Send slower.” “Right. Right.” In fact, Shannon showed that the beleaguered key-tappers in Ireland and Newfoundland had essentially gotten it right, had already solved the problem without knowing it. They might have said, if only they could have read Shannon’s paper, “Please add redundancy.”
In a way, that was already evident enough: Saying the same thing twice in a noisy room is a way of adding redundancy, on the unstated assumption that the same error is unlikely to attach itself to the same place two times in a row. For Shannon, though, there was much more. Our linguistic predictability, our congenital failure to maximize information, is actually our best protection from error. For Shannon the key was in the code. We must be able to write codes, he showed, in which redundancy acts as a shield: codes in which no one bit is indispensable, and thus codes in which any bit can absorb the damage of noise.
Shannon did not produce the codes in his 1948 paper, but he proved that they must exist. The secret to accurate communication was not yelling across a crowded room, not hooking up more spark coils to the telegraph, not beaming twice the television signal into the sky. We only had to signal smarter.
As long as we respect the speed limit of the channel, there is no limit to our accuracy, no limit to the amount of noise through which we can make ourselves heard. Any message could be sent flawlessly—we could communicate anything of any complexity to anyone at any distance—provided it was translated into 1’s and 0’s.
Just as all systems of communication have an essential structure in common, all of the messages they send have a digital kinship. “Up until that time, everyone thought that communication was involved in trying to find ways of communicating written language, spoken language, pictures, video, and all of these different things—that all of these would require different ways of communicating,” said Shannon’s colleague Robert Gallager. “Claude said no, you can turn all of them into binary digits. And then you can find ways of communicating the binary digits.” You can code any message as a stream of bits, without having to know where it will go; you can transmit any stream of bits, efficiently and reliably, without having to know where it came from. As information theorist Dave Forney put it, “bits are the universal interface.”
In time, the thoughts developed in Shannon’s 77 pages in the Bell System Technical Journal would give rise to a digital world: satellites speaking to earth in binary code, discs that could play music through smudges and scratches (because storage is just another channel, and a scratch is just another noise), the world’s information distilled into a black rectangle two inches across.
Shannon would live to see “information” turn from the name of a theory to the name of an era. “The Magna Carta of the Information Age,” Scientific American would call his 1948 paper decades later. “Without Claude’s work, the internet as we know it could not have been created,” ran a typical piece of praise. And on and on: “A major contribution to civilization.” “A universal clue to solving problems in different fields of science.” “I reread it every year, with undiminished wonder. I’m sure I get an IQ boost every time.” “I know of no greater work of genius in the annals of technological thought.”
Shannon turned 32 in 1948. The conventional wisdom in mathematical circles had long held that 30 is the age by which a young mathematician ought to have accomplished his foremost work; the professional mathematician’s fear of aging is not so different from the professional athlete’s. “For most people, thirty is simply the dividing line between youth and adulthood,” writes John Nash biographer Sylvia Nasar, “but mathematicians consider their calling a young man’s game, so thirty signals something far more gloomy.”
Shannon was two years late by that standard, but he had made it.
Jimmy Soni is an author, editor, and former speechwriter.
Rob Goodman is a doctoral candidate at Columbia University and a former congressional speechwriter.
From A Mind at Play by Jimmy Soni and Rob Goodman. Copyright © 2017 by Jimmy Soni and Rob Goodman. Reprinted by permission of Simon & Schuster, Inc.