Scientific progress is not usually straightforward. Researchers pursue and abandon lines of inquiry. Results languish. Theories take decades to cohere.
But sometimes the accumulation of scientific knowledge proceeds more directly, with one discovery triggering the next like a cascade of dominoes.
That’s been the case recently with the mathematical study of fluid mechanics. A startling experimental discovery in 2013 set in motion a series of mathematical proofs that have unsettled centuries of thinking.
“It’s been a very dynamic and exciting story,” said Alexander Kiselev, a mathematician at Duke University and a coauthor of one of the proofs.
The discoveries center on the Euler equations, posed by Leonhard Euler in 1757. Mathematicians and physicists have used them to model how fluids evolve over time. If you toss a rock into a still pond, how will the water be moving five seconds later? The Euler equations can tell you.
Though, not literally. The Euler equations describe an idealized world in which fluids have a number of properties not found in reality. The equations assume, for example, that fluids have no viscosity (internal currents don’t create friction as they move past one another) and that they’re incompressible (you can’t squeeze a fluid into a smaller space than it already occupies).
Within this idealized world, the equations use Newton’s laws of motion to predict the future states of a fluid. Ultimately, mathematicians who study the Euler equations want to know whether the equations always work. Are there scenarios that effectively cause the equations to crash and prevent them from describing a fluid any further into the future?
In 2013, a pair of mathematicians seemed to find such a scenario. Thomas Hou of the California Institute of Technology and Guo Luo, now of the City University of Hong Kong, were running numerical simulations on a computer. They provided a numerical description of the initial state of a fluid and let the computer apply the Euler equations to determine the fluid’s motion in the future.
Hou and Luo focused on a particular scenario that you could nearly simulate at home. But first, to help think about the surprisingly complicated ways in which fluids can flow, let’s consider a scenario you really can try at home.
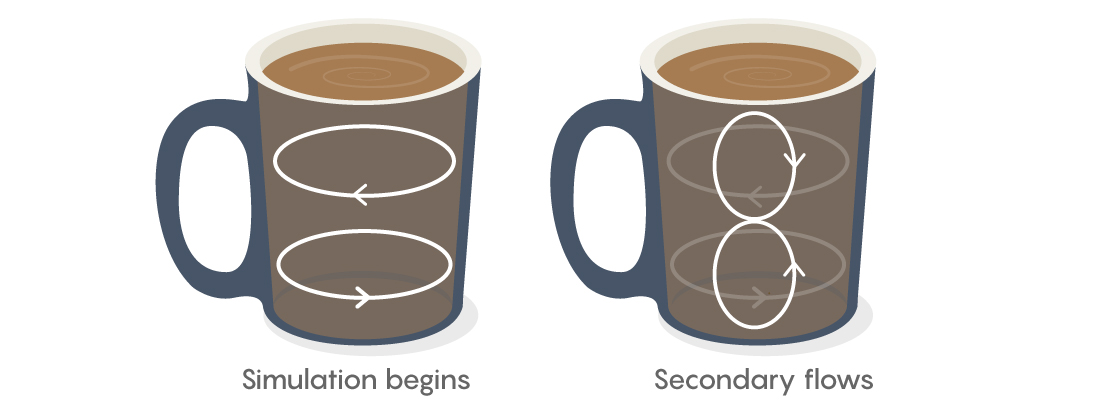
Imagine a flat-bottomed, cylindrical cup full of tea, with some tea leaves that have settled at the bottom. Now stir the tea clockwise. At first the whole fluid rotates almost as a single body, sweeping the leaves along for the ride.
As the stirring proceeds, though, the centrifugal force of the rotating liquid interacts with the side of the cup to create what physicists call a “secondary flow” — a more complicated motion that arises in response to the initial motion of the stirring. These secondary flows, which go down at the sides of the cylinder and up at the center, are evident in the motion of the tea leaves: They collect in the center at the bottom of the cup and then remain practically stationary even as the tea around them continues to swirl.
The phenomenon, observed for centuries, is called the “tea leaf paradox.” In 1926 Albert Einstein provided the first mathematical explanation for this behavior.

The scenario that Hou and Luo considered is slightly more complicated. Again, imagine a fluid in a cylinder. This time, the fluid in the top half of the cylinder is rotating clockwise, as in the tea cup, but in the bottom half it’s rotating counterclockwise. The motions produce several secondary flows. Eddies develop, in the form of swirls running up and down the sides of the cylinder.
“From the top the fluid is spiraling down, and from the bottom it is swirling up in the opposite direction,” Hou said.
As Hou and Luo ran their numerical simulation, they observed something surprising happening halfway down the cup, right where the conflicting flows came together. The Euler equations reported that the vorticity (or spin) of the fluid at that point was amplifying dramatically. In fact, their simulation showed that according to the Euler equations, the vorticity at that point was growing so fast that it was on track to become infinite in a finite amount of time.
Such infinite values are known as singularities. If the Euler equations were to produce a singularity, they’d break down — mathematicians call it “blowing up” — and would no longer be able to describe the future motion of a fluid. This is because the equations can’t compute with infinite quantities.
Hou and Luo’s discovery caused a sensation. For more than 200 years, mathematicians had hunted for scenarios in which the Euler equations faltered. Many had performed numerical simulations that they thought were on track to produce singularities, but none held up under repeated experimentation with faster computers. Hou and Luo finally seemed to have found one that would stick.
“Many researchers believe that this is the most convincing singularity scenario we have,” said Vladimir Sverak of the University of Minnesota.
But a computer simulation is merely evidence. It’s not a proof.
“Computers are limited in the sense that they cannot go to the infinitesimal scale,” Kiselev said. “The result could look very convincing, but you don’t know. Maybe if you get a better supercomputer … you see things start to disintegrate.”
So mathematicians rushed to see if they could prove that what Hou and Luo had observed was really occurring mathematically.

Kiselev and Sverak learned about the simulation in 2013, during a presentation by Hou at a summer workshop at Stanford University. It prompted them to begin working on an important open problem about the rate at which vorticity grows in two-dimensional fluids. They managed to prove a long-conjectured property of the growth rate by considering a version of the scenario Hou and Luo had used in their simulation.
Mathematicians had spent a long time searching for such a useful scenario — Hou and Luo’s simulation suggested to Kiselev and Sverak where they might find one.
“It was sort of like having a target to aim for,” Kiselev said. “It’s one thing if you’re hunting and you don’t even see your target. It’s another thing when you know where it is.”
Subsequent proofs over the years have extended the mathematical understanding of singularity formation in the Euler equations. In 2019, Tarek Elgindi of the University of California, San Diego, (along with his collaborators Tej-eddine Ghoul and Nader Masmoudi) published two proofs detailing circumstances in which the Euler equations produced singularities. The earlier paper by Kiselev and Sverak was one of the starting points for his work.
Elgindi’s proofs involve slightly specialized conditions and fall short of the complete understanding of singularity formation within the Euler equations that mathematicians seek. Still, they are among the strongest results ever achieved in the discipline. Quanta described the work in our recent feature “Famous Fluid Equations Spring a Leak.”
In the same way that eddies in a stream alter downstream currents, Elgindi’s work itself prompted a new round of mathematical discovery. In October 2019, Hou and Jiajie Chen adapted some of Elgindi’s methods to create a rigorous mathematical proof of a scenario closely related to the one in the 2013 experiment. They proved that in this slightly modified scenario, the singularity they’d observed forming in the Euler equations really does occur.
“They took [Elgindi’s] ideas and applied them to the scenario from 2013,” Sverak said. The circle was complete.
There’s still more work to be done, of course. Hou’s new proof has some technical qualifications that prevent it from establishing the existence of the singularity in the exact situation he modeled in 2013. But after a remarkable six-year run and with renewed momentum, Hou believes he’ll soon surmount those challenges, too.
“I think we’re very close,” he said.
Lead image: The complicated currents in a cup of tea inspired a series of important proofs. Credit: Lucy Reading-Ikkanda/Quanta Magazine