The most powerful formula in physics starts with a slender S, the symbol for a sort of sum known as an integral. Further along comes a second S, representing a quantity known as action. Together, these twin S’s form the essence of an equation that is arguably the most effective diviner of the future yet devised.
The oracular formula is known as the Feynman path integral. As far as physicists can tell, it precisely predicts the behavior of any quantum system—an electron, a light ray, or even a black hole. The path integral has racked up so many successes that many physicists believe it to be a direct window into the heart of reality.
“It’s how the world really is,” said Renate Loll, a theoretical physicist at Radboud University in the Netherlands.
But the equation, although it graces the pages of thousands of physics publications, is more of a philosophy than a rigorous recipe. It suggests that our reality is a sort of blending—a sum—of all imaginable possibilities. But it does not tell researchers exactly how to carry out the sum. So physicists have spent decades developing an arsenal of approximation schemes for constructing and computing the integral for different quantum systems.
The approximations work well enough that intrepid physicists like Loll are now pursuing the ultimate path integral: one that blends all conceivable shapes of space and time and produces a universe shaped like ours as the net result. But in this quest to show that reality is indeed the sum of all possible realities, they face deep confusion about which possibilities should enter the sum.
All Roads Lead to One
Quantum mechanics really got off the ground in 1926 when Erwin Schrödinger devised an equation describing how the wavelike states of particles evolve from moment to moment. The next decade, Paul Dirac advanced an alternative vision of the quantum world. His was based on the venerable notion that things take the path of “least action” to get from A to B—the route that, loosely speaking, takes the least time and energy. Richard Feynman later stumbled upon Dirac’s work and fleshed out the idea, unveiling the path integral in 1948.
The heart of the philosophy is on full display in the quintessential quantum mechanics demonstration: the double-slit experiment.
Physicists fire particles at a barrier with two slits in it and observe where the particles land on a wall behind the barrier. If particles were bullets, they’d form a cluster behind each slit. Instead, particles land along the back wall in repeating stripes. The experiment suggests that what moves through the slits is actually a wave representing the particle’s possible locations. The two emerging wavefronts interfere with each other, producing a series of peaks where the particle might end up being detected.
The interference pattern is a supremely strange result because it implies that both of the particle’s possible paths through the barrier have a physical reality.
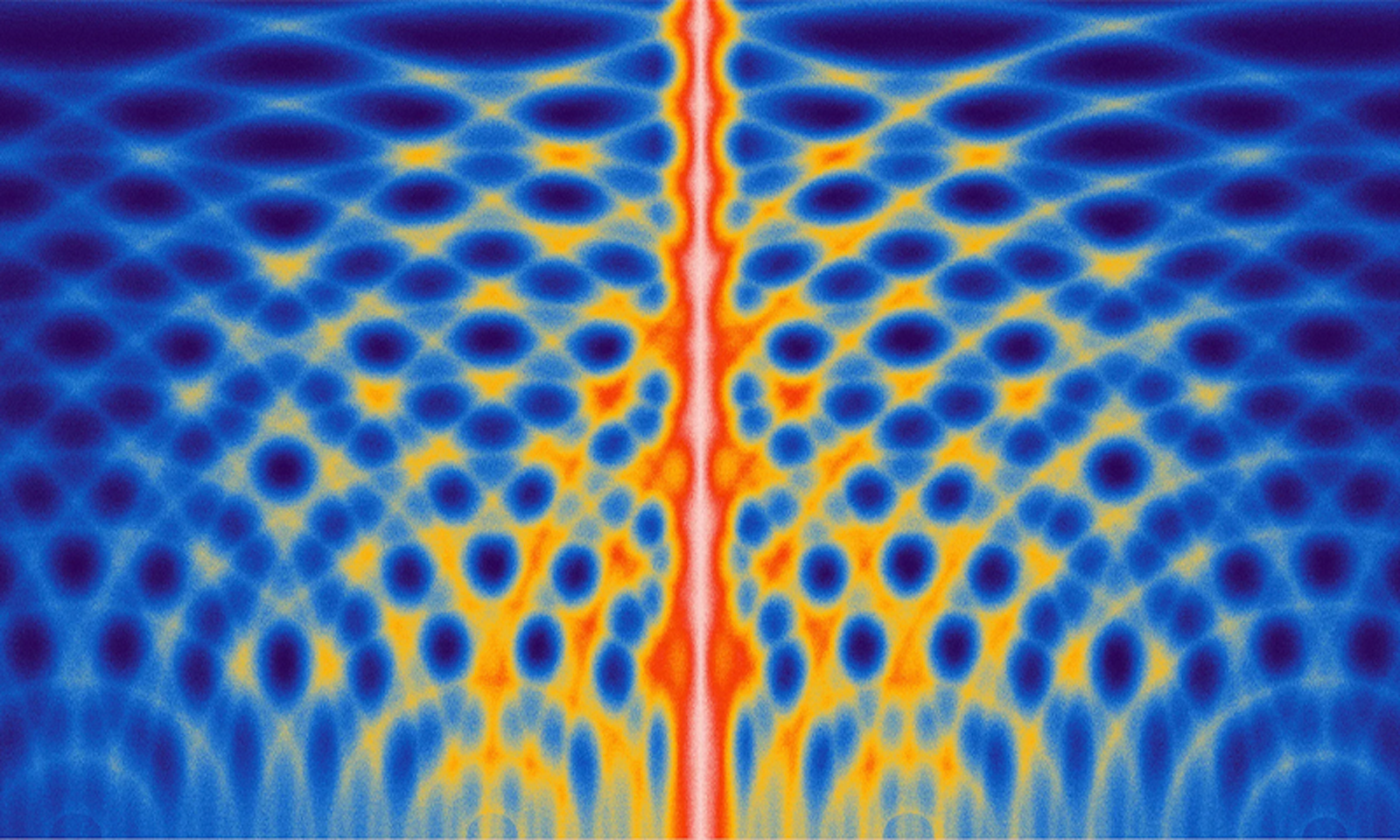
The path integral assumes this is how particles behave even when there are no barriers or slits around. First, imagine cutting a third slit in the barrier. The interference pattern on the far wall will shift to reflect the new possible route. Now keep cutting slits until the barrier is nothing but slits. Finally, fill in the rest of space with all-slit “barriers.” A particle fired into this space takes, in some sense, all routes through all slits to the far wall—even bizarre routes with looping detours. And somehow, when summed correctly, all those options add up to what you’d expect if there are no barriers: a single bright spot on the far wall.
It’s a radical view of quantum behavior that many physicists take seriously. “I consider it completely real,” said Richard MacKenzie, a physicist at the University of Montreal.
But how can an infinite number of curving paths add up to a single straight line? Feynman’s scheme, roughly speaking, is to take each path, calculate its action (the time and energy required to traverse the path), and from that get a number called an amplitude, which tells you how likely a particle is to travel that path. Then you sum up all the amplitudes to get the total amplitude for a particle going from here to there—an integral of all paths.
Naïvely, swerving paths look just as likely as straight ones, because the amplitude for any individual path has the same size. Crucially, though, amplitudes are complex numbers. While real numbers mark points on a line, complex numbers act like arrows. The arrows point in different directions for different paths. And two arrows pointing away from each other sum to zero.
The upshot is that, for a particle traveling through space, the amplitudes of more or less straight paths all point essentially in the same direction, amplifying each other. But the amplitudes of winding paths point every which way, so these paths work against each other. Only the straight-line path remains, demonstrating how the single classical path of least action emerges from unending quantum options.
Feynman showed that his path integral is equivalent to Schrödinger’s equation. The benefit of Feynman’s method is a more intuitive prescription for how to deal with the quantum world: Sum up all the possibilities.
Sum of All Ripples
Physicists soon came to understand particles as excitations in quantum fields—entities that fill space with values at every point. Where a particle might move from place to place along different paths, a field might ripple here and there in different ways.
Fortunately, the path integral works for quantum fields, too. “It’s obvious what to do,” said Gerald Dunne, a particle physicist at the University of Connecticut. “Instead of summing over all paths, you sum over all configurations of your fields.” You identify the field’s initial and final arrangements, then consider every possible history that links them.
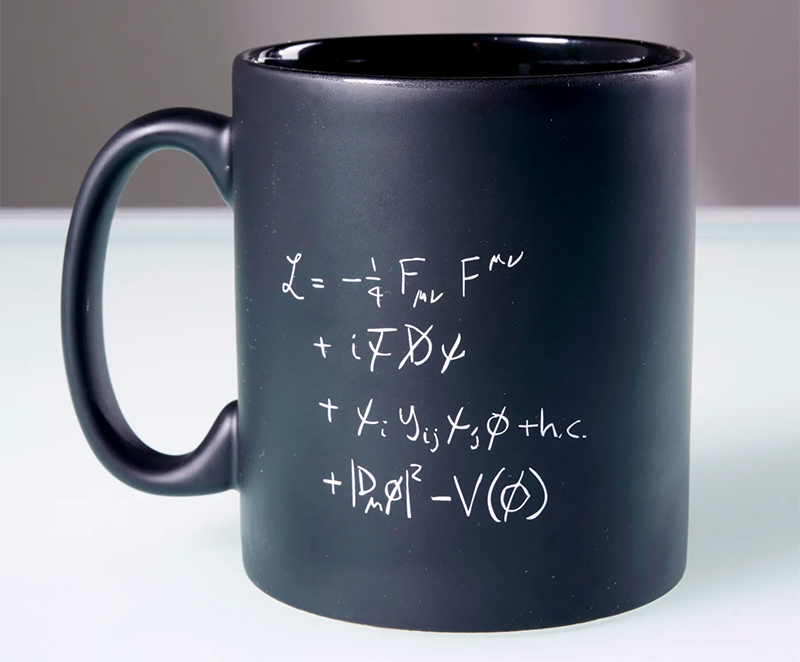
Feynman himself leaned on the path integral to develop a quantum theory of the electromagnetic field in 1949. Others would work out how to calculate actions and amplitudes for fields representing other forces and particles. When modern physicists predict the outcome of a collision at the Large Hadron Collider in Europe, the path integral underlies many of their computations. The gift shop there even sells a coffee mug displaying an equation that can be used to calculate the path integral’s key ingredient: the action of the known quantum fields.
“It’s absolutely fundamental to quantum physics,” Dunne said.
Despite its triumph in physics, the path integral makes mathematicians queasy. Even a simple particle moving through space has infinitely many possible paths. Fields are worse, with values that can change in infinitely many ways in infinitely many places. Physicists have clever techniques for coping with the teetering tower of infinities, but mathematicians argue that the integral was never designed to operate in such an infinite environment.
“It’s like black magic,” said Yen Chin Ong, a theoretical physicist at Yangzhou University in China who has a background in mathematics. “Mathematicians are not comfortable working with things where it’s not clear what’s going on.”
Yet it gets results that are beyond dispute. Physicists have even managed to estimate the path integral for the strong force, the extraordinarily complex interaction that holds together particles in atomic nuclei. They used two main hacks to do this. First, they made time an imaginary number, a strange trick that turns amplitudes into real numbers. Then they approximated the infinite spacetime continuum as a finite grid. Practitioners of this “lattice” quantum field theory approach can use the path integral to calculate properties of protons and other particles that feel the strong force, overcoming rickety mathematics to get solid answers that match experiments.
“To someone like me in particle physics,” Dunne said, “that’s the proof that the thing works.”
Spacetime = The Sum of What?
The greatest mystery in fundamental physics, however, sits beyond experimental reach. Physicists wish to understand the quantum origin of the force of gravity. In 1915, Albert Einstein recast gravity as the result of curves in the fabric of space and time. His theory revealed that the length of a measuring stick and the tick of a clock change from place to place—that spacetime is a malleable field, in other words. Other fields have a quantum nature, so most physicists expect that spacetime should too, and that the path integral should capture that behavior.
Feynman’s philosophy is clear: Physicists should sum over all possible shapes of spacetime. But when we consider the shape of space and time, exactly what is possible?
Spacetime might conceivably split, for instance, severing one location from another. Or it might become punctured by tubes—wormholes—that link locations together. Einstein’s equations allow for such exotic shapes, but forbids changes that would lead to them; rips or mergers would violate causality and raise time travel paradoxes. No one knows whether spacetime and gravity might engage in more daring activity at the quantum level, however, so physicists don’t know whether to throw Swiss-cheese spacetimes into the “gravitational path integral” or not.
One camp suspects that everything goes in. Stephen Hawking, for instance, championed a path integral that accommodates rips, wormholes, doughnuts, and other wild “topological” changes between shapes of space. He leaned on the imaginary-number hack for time to make the math easier. Making time imaginary effectively turns it into another dimension of space. In such a timeless arena there’s no notion of causality for wormhole-ridden or ripped universes to spoil. Hawking used this timeless, “Euclidean” path integral to argue that time began at the Big Bang and to count the spacetime building blocks inside a black hole. Recently, researchers used the Euclidean approach to argue that information leaks out of dying black holes.
This “seems to be the richer point of view to take,” said Simon Ross, a quantum gravity theorist at Durham University. “The gravitational path integral, defined to include all of the topologies, has some beautiful properties that we don’t fully understand yet.”
But the richer perspective comes at a price. Some physicists dislike removing a load-bearing element of reality such as time. The Euclidean path integral “is really completely unphysical,” Loll said.
Her camp endeavors to keep time in the path integral, situating it in the spacetime we know and love, where causes strictly precede effects. After spending years developing ways to approximate this much more formidable path integral, Loll has found hints that the approach can work. In one paper, for instance, she and her collaborators added up a bunch of standard spacetime shapes (approximating each one as a quilt of tiny triangles) and got something like our universe—the spacetime equivalent of showing that particles move in straight lines.
Others are advancing the timeless path integral for spacetime and gravity, with all topological changes included. In 2019, researchers rigorously defined the full integral—not just an approximation—for two-dimensional universes, but using mathematical tools that further muddied its physical meaning. Such work only deepens the impression, among physicists and mathematicians alike, that the path integral holds power that’s waiting to be harnessed. “Perhaps we are still yet to make path integrals well defined,” Ong said, “but fundamentally I think it’s just a matter of time.”
This article was originally published on the Quanta Abstractions blog.
Lead image: A particle’s straight-line path through space can be understood as the sum of all its possible paths. Credit: Kristina Armitage / Quanta Magazine.