When Lisa Piccirillo solved a decades-old mystery about the “Conway knot,” she had to overcome the knot’s uncanny ability to hoodwink some of the most powerful tools mathematicians have devised. Known as invariants, these tools form the backbone not just of knot theory but of many areas of mathematics, extracting essential features of mathematical objects and detecting when two objects are fundamentally different from each other.
As the name suggests, an invariant is an attribute that doesn’t vary as you change an object’s inessential features (where “inessential” means whatever you need it to in a particular context). An invariant is a distillation of some innate quality of the object, often in the form of a single number.
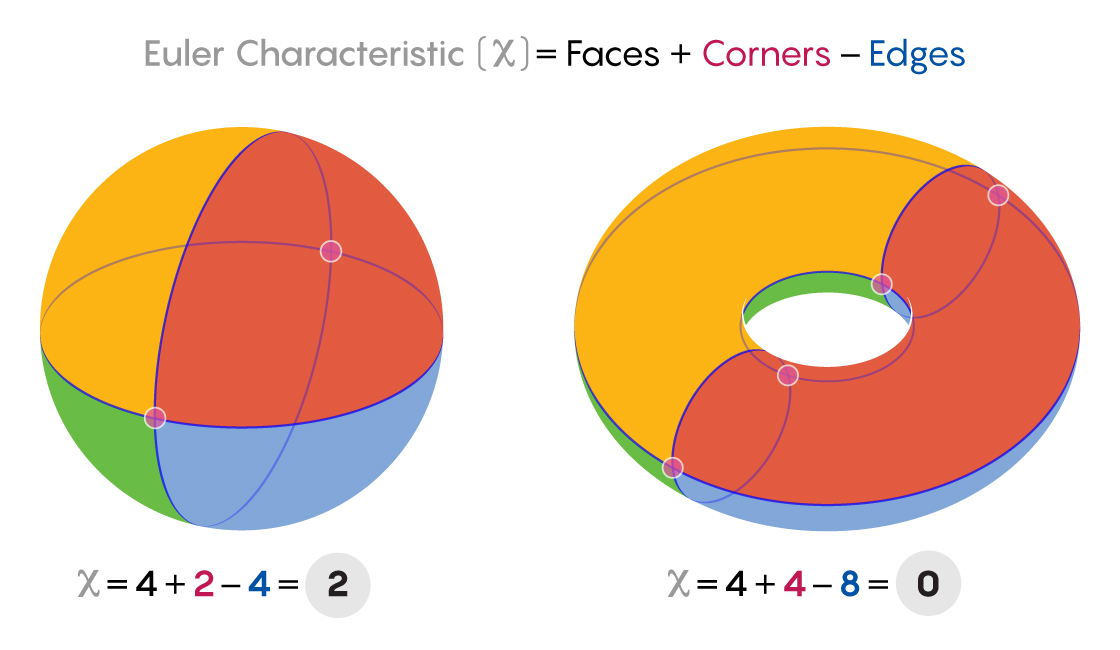
To take an example from topology, imagine covering a ball with stretchy netting that partitions the surface into shapes such as triangles and rectangles. The number of shapes will, of course, depend on the netting you use, as will the numbers of edges and corners. But mathematicians figured out centuries ago that a certain combination of these three numbers always comes out the same: the number of shapes plus the number of corners minus the number of edges.
If, for example, your netting partitions the sphere into a puffed-out tetrahedron (with four triangles, four corners and six edges), this number works out to 4 + 4 − 6 = 2. If your netting instead forms the pattern of a soccer ball (with a total of 32 hexagons and pentagons, 60 corners, and 90 edges), you again get 32 + 60 − 90 = 2. In some sense, the number 2 is an intrinsic feature of sphere-ness. This number (called the sphere’s Euler characteristic) doesn’t change if you stretch or distort the sphere, so it is what mathematicians call a topological invariant.
If you wrap a netting around a doughnut surface instead, you always get an Euler characteristic of 0. On a two-holed doughnut, you get −2. The Euler characteristic for surfaces belongs to a series of invariants that allow mathematicians to explore shapes in higher dimensions as well. It can help topologists distinguish between two shapes that are hard to visualize, since if they have different Euler characteristics, they cannot be the same topological shape.
Invariants are also used to study the 15-puzzle, a classic toy consisting of square tiles numbered 1 through 15 that you slide around in a 4-by-4 grid. The goal is to put a mixed-up arrangement of tiles in numerical order from left to right, starting from the top row. If you’d like to know whether a particular arrangement is solvable, there’s an invariant that gives you the answer. It outputs either “even” or “odd” depending on the sum of two numbers: the number of slides required to carry the blank square to the bottom right corner and the number of tile pairings that are in reverse numerical order (with the blank square representing tile 16).
Whenever you slide a tile into the empty square, both these numbers switch parity (evenness or oddness). So the parity of their sum never changes, meaning that it is an invariant of the sliding process. For the solved configuration this invariant is even, since both numbers are zero. So any configuration with an odd invariant is utterly hopeless.
When it comes to knot theory, distinguishing between knots is a tricky business, since you can make a knot unrecognizable just by moving the strands of the loop around (mathematicians think of knots as occurring in closed loops rather than open strings, so they can’t be undone). Here, invariants are indispensable, and mathematicians have come up with dozens that distill different features of knots. But these invariants tend to have blind spots.
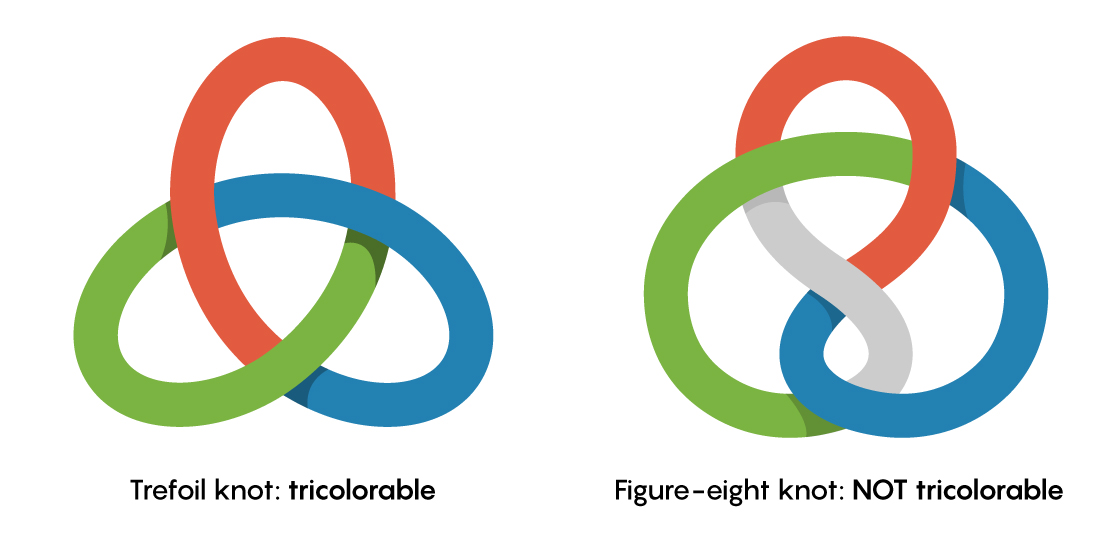
Take, for example, an invariant called tricolorability. A knot diagram is tricolorable if there’s a way to color its strands red, blue and green so that at every crossing, the three strands that meet are either all the same color or all different colors. Mathematicians have shown that even when you move the strands of a knot around, its tricolorability (or lack thereof) is unchanged. In other words, tricolorability is an innate feature of a knot.
The three-crossing knot known as the trefoil is tricolorable. But the “unknot” (a loop that has no actual knots, even if it appears tangled) is not tricolorable, providing an instant proof that the trefoil is not just the unknot in disguise. But while tricolorability enables us to distinguish some knots from the unknot, it’s not a perfect tool for this purpose: Knots that are tricolorable are definitely knotted, but knots that aren’t tricolorable aren’t definitely unknotted. For instance, the figure-eight knot is not tricolorable, but it is genuinely knotted. This knot falls into tricolorability’s blind spot—it’s as if the invariant is saying, “The figure-eight knot is unknotted as far as I can tell.”
The Conway knot, an 11-crossing knot discovered by John Horton Conway more than 50 years ago, is extraordinarily skilled at fooling knot invariants—especially the ones designed to detect the quality Piccirillo was interested in, called sliceness. Sliceness means that the knot is a slice of some smooth but knotted sphere in four-dimensional space.
“Every time there’s a new invariant, people look to see what happens on the Conway knot,” said Shelly Harvey of Rice University. So far, the Conway knot has fallen in the blind spot of every invariant mathematicians have come up with to study sliceness.
When Piccirillo finally succeeded in showing that the Conway knot is not “slice,” she did so not by devising a new invariant but by finding a clever way to leverage an existing one called Rasmussen’s s-invariant. The Conway knot fools this invariant along with all the others. But in her paper, Piccirillo came up with a different knot that she could prove to have the same slice status as the Conway knot. For this new knot, Rasmussen’s s-invariant proves that it is not slice. Therefore, the Conway knot cannot be slice either.
Rasmussen’s s-invariant is one of a collection of physics-related knot invariants discovered in recent decades. It has taken mathematicians a while to absorb what these invariants have to offer, said Elisenda Grigsby of Boston College.
Piccirillo is part of a “new guard of low-dimensional topologists that have grown up knowing [these invariants] in their bones,” Grigsby said. “To me, that’s what’s exciting about this paper.