Even though mathematicians have spent over 2,000 years dissecting the structure of the five Platonic solids—the tetrahedron, cube, octahedron, icosahedron and dodecahedron—there’s still a lot we don’t know about them.
Now, a trio of mathematicians has resolved one of the most basic questions about the dodecahedron.
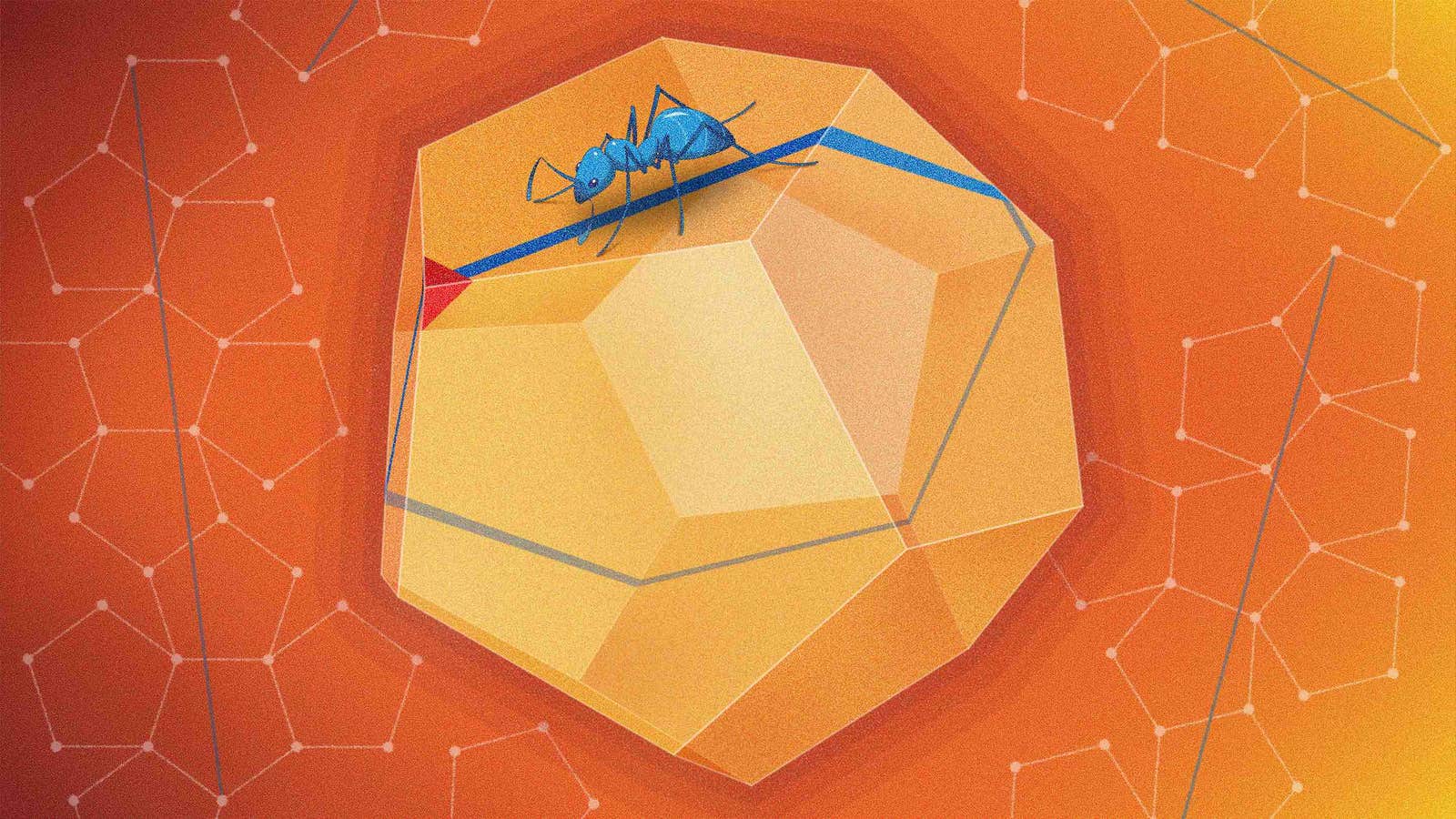
Suppose you stand at one of the corners of a Platonic solid. Is there some straight path you could take that would eventually return you to your starting point without passing through any of the other corners? For the four Platonic solids built out of squares or equilateral triangles—the cube, tetrahedron, octahedron and icosahedron—mathematicians figured out that the answer is no. Any straight path starting from a corner will either hit another corner or wind around forever without returning home. But with the dodecahedron, which is formed from 12 pentagons, mathematicians didn’t know what to expect.
Now Jayadev Athreya, David Aulicino and Patrick Hooper have shown that an infinite number of such paths do in fact exist on the dodecahedron. Their paper, published in May 2020 in Experimental Mathematics, shows that these paths can be divided into 31 natural families.
The solution required modern techniques and computer algorithms. “Twenty years ago, [this question] was absolutely out of reach; 10 years ago it would require an enormous effort of writing all necessary software, so only now all the factors came together,” wrote Anton Zorich, of the Institute of Mathematics of Jussieu in Paris, in an email.
The project began in 2016 when Athreya, of the University of Washington, and Aulicino, of Brooklyn College, started playing with a collection of card stock cutouts that fold up into the Platonic solids. As they built the different solids, it occurred to Aulicino that a body of recent research on flat geometry might be just what they’d need to understand straight paths on the dodecahedron. “We were literally putting these things together,” Athreya said. “So it was kind of idle exploration meets an opportunity.”
Together with Hooper, of the City College of New York, the researchers figured out how to classify all the straight paths from one corner back to itself that avoid other corners.
Their analysis is “an elegant solution,” said Howard Masur of the University of Chicago. “It’s one of these things where I can say, without any hesitation, ‘Goodness, oh, I wish I had done that!’”
Hidden Symmetries
Although mathematicians have speculated about straight paths on the dodecahedron for more than a century, there’s been a resurgence of interest in the subject in recent years following gains in understanding “translation surfaces.” These are surfaces formed by gluing together parallel sides of a polygon, and they’ve proved useful for studying a wide range of topics involving straight paths on shapes with corners, from billiard table trajectories to the question of when a single light can illuminate an entire mirrored room.
In all these problems, the basic idea is to unroll your shape in a way that makes the paths you are studying simpler. So to understand straight paths on a Platonic solid, you could start by cutting open enough edges to make the solid lie flat, forming what mathematicians call a net. One net for the cube, for example, is a T shape made of six squares.

Imagine that we’ve flattened out the dodecahedron, and now we’re walking along this flat shape in some chosen direction. Eventually we’ll hit the edge of the net, at which point our path will hop to a different pentagon (whichever one was glued to our current pentagon before we cut open the dodecahedron). Whenever the path hops, it also rotates by some multiple of 36 degrees.
To avoid all this hopping and rotating, when we hit an edge of the net we could instead glue on a new, rotated copy of the net and continue straight into it. We’ve added some redundancy: Now we have two different pentagons representing each pentagon on the original dodecahedron. So we’ve made our world more complicated—but our path has gotten simpler. We can keep adding a new net each time we need to expand beyond the edge of our world.
By the time our path has traveled through 10 nets, we’ve rotated our original net through every possible multiple of 36 degrees, and the next net we add will have the same orientation as the one we started with. That means this 11th net is related to the original one by a simple shift—what mathematicians call a translation. Instead of gluing on an 11th net, we could simply glue the edge of the 10th net to the corresponding parallel edge in the original net. Our shape will no longer lie flat on the table, but mathematicians think of it as still “remembering” the flat geometry from its previous incarnation—so, for instance, paths are considered straight if they were straight in the unglued shape. After we do all such possible gluings of corresponding parallel edges, we end up with what is called a translation surface.

The resulting surface is a highly redundant representation of the dodecahedron, with 10 copies of each pentagon. And it’s massively more complicated: It glues up into a shape like a doughnut with 81 holes. Nevertheless, this complicated shape allowed the three researchers to access the rich theory of translation surfaces.
To tackle this giant surface, the mathematicians rolled up their sleeves—figuratively and literally. After working on the problem for a few months, they realized that the 81-holed doughnut surface forms a redundant representation not just of the dodecahedron but also of one of the most studied translation surfaces. Called the double pentagon, it is made by attaching two pentagons along a single edge and then gluing together parallel sides to create a two-holed doughnut with a rich collection of symmetries.
This shape also happened to be tattooed on Athreya’s arm. “The double pentagon was something that I already knew and loved,” said Athreya, who got the tattoo a year before he and Aulicino started thinking about the dodecahedron.
Because the double pentagon and the dodecahedron are geometric cousins, the former’s high degree of symmetry can elucidate the structure of the latter. It’s an “amazing hidden symmetry,” said Alex Eskin of the University of Chicago (who was Athreya’s doctoral adviser about 15 years ago). “The fact that the dodecahedron has this hidden symmetry group is, I think, quite remarkable.”
The relationship between these surfaces meant that the researchers could tap into an algorithm for analyzing highly symmetric translation surfaces developed by Myriam Finster of the Karlsruhe Institute of Technology in Germany. By adapting Finster’s algorithm, the researchers were able to identify all the straight paths on the dodecahedron from a corner to itself, and to classify these paths via the dodecahedron’s hidden symmetries.
The analysis was “one of the most fun projects I’ve gotten to work on in my whole career,” Athreya said. “It’s important to keep playing with things.”
The new result shows that even objects that have been studied for thousands of years can still hold secrets, Eskin said. “I think even for [the three mathematicians], it was very, very surprising to say something new about the dodecahedron.”
Lead image: Samuel Velasco/Quanta Magazine
Video: In this Numberphile episode, Jayadev Athreya explains how he and his colleagues solved a longstanding problem about straight paths on a dodecahedron.