Facebook
Twitter
Pocket
Reddit
Email
Elliptic curves seem to admit infinite variety, but they really only come in two flavors. That is the upshot of a new proof from a graduate student at Harvard University.
Elliptic curves may sound exotic, but they’re unspectacular geometric objects, as ordinary as lines, parabolas, or ellipses. In a paper first posted online last year, Alexander Smith proved a four-decade-old conjecture that concerns a fundamental trait of elliptic curves called “rank.” Smith proved that, within a specific family of curves, and with one qualification, half of all curves have rank 0 and half have rank 1.
The result establishes baseline characteristics of objects that have intrigued mathematicians for centuries, and that have increased in importance in recent decades.
“We’ve been thinking about this for over 1,000 years, and now we have some probabilistic sense about [elliptic curves]. That’s super important,” said Shou-Wu Zhang, a mathematician at Princeton University who advised Smith at the outset of the work, when Smith was an undergraduate at Princeton.
Elliptic curves are equations with a variable raised to the third power, like y2 = x3 + 1. They’ve figured in many important mathematical proofs in recent decades, including Andrew Wiles’ landmark 1994 proof of Fermat’s Last Theorem. They’re powerful in part because they’re the most complicated type of polynomial equation about which mathematicians have some systematic understanding.
“Elliptic curves are sort of the most interesting case,” said Dorian Goldfeld, a mathematician at Columbia University who proposed the eponymous Goldfeld conjecture in 1979.
The Goldfeld conjecture makes a prediction about the ranks of elliptic curves. As Quanta explained in a recent article, “Without a Proof, Mathematicians Wonder How Much Evidence Is Enough,” rank is a measure of the complexity of the curve’s set of rational solutions (solutions that can be expressed as fractions). While there is no proven limit to how high the rank of a curve can be—the highest-ranked curve mathematicians have found has a rank of 28—the Goldfeld conjecture predicts that, overall, half of all elliptic curves have rank 0 and half have rank 1.
You may be wondering how it’s possible for there to be elliptic curves with rank higher than 1 if half of all elliptic curves have a rank of 0 and half have a rank of 1. After all, if you have a box full of pingpong balls, and you know that exactly half are black and half are white, you know that there can’t be any red ones hiding in there.
Even more perplexing, there aren’t just a few elliptic curves with a rank of 2 or higher, but an infinite number of them. The apparent absurdity is a result of the slippery statistics involved in infinity. Even though there are lots of curves of rank 2 or higher, there are so many more curves of ranks 0 and 1 that curves of rank 2 or higher are statistically insignificant. If you were to put all the curves in a box and pick one out at random, your odds of picking a curve with a rank higher than 1 are officially zero.
What does it mean for a curve to have a rank of 0? These curves have a finite number of rational points—in fact, no more than 16, as proved by Barry Mazur in the 1970s.
There are reasons to think lots of elliptic curves would have rank 0. If you picture a curve carving its way through the plane, most of the points on the curve are not rational. Those points can’t be expressed as fractions, no matter how elaborate. The chances that a randomly drawn curve would intersect lots of rational points—infinitely many—are low.
“My philosophy about this is that if you look at a random elliptic curve, it has a good reason to be rank 0. It doesn’t want to have rational points,” Smith said.
The ubiquity of rank 1 curves has a similar explanation. Rank 1 curves have infinitely many rational points, but all those points line up in a neat way, so that you can connect the dots between them using a relatively straightforward procedure.
Curves of rank 2 or higher have more complicated sets of rational points. These need to contain multiple infinite subsets of rational points that don’t connect with one another.
“What’s the chance of having two independent points?” Goldfeld said. “It seems to be very hard. My conjecture says it should happen rarely.”
When Goldfeld first made his conjecture, most mathematicians thought it was false. They pointed to computational experiments that suggested that curves with rank 2 or higher occur far more often than 0 percent of the time.
Goldfeld replied that they just weren’t casting their nets wide enough. He pointed out that if you only studied the first 10 whole numbers, you’d come to the wildly inaccurate estimate that 40 percent of all whole numbers are prime. In a similar fashion, these computational experiments were extrapolating from small subsets of elliptic curves to infinitely large families of curves.
“I said, ‘Look at the primes!’ That was my response. You have to go much, much higher because at the beginning there could be a lot of funny things appearing,” Goldfeld said.
Alexander Smith has shown that Goldfeld was right. In his new paper, he proves that 100 percent of elliptic curves* have rank 0 or 1. He also proves that those curves are split equally between the two ranks, though this step comes with a caveat. His proof of the 50-50 split is contingent on the Birch and Swinnerton-Dyer (BSD) conjecture being true. The BSD conjecture is one of the most famous open problems in math. Mathematicians are far from proving it, but they generally believe it’s true.
Even with that caveat, Smith’s result is being received as momentous. Mathematicians say it indicates a way to fully prove the Goldfeld conjecture without having to tackle the daunting BSD conjecture. It does so by providing a new understanding of the underlying nature of elliptic curves.
“Alex Smith’s work is extremely exciting and I think still yet to be fully studied and appreciated,” said Melanie Wood, a mathematician at the University of Wisconsin, Madison. “It is a very important and groundbreaking thing to have been able to do.”
* The Goldfeld conjecture is not about elliptic curves generally. Instead, it’s about special families of elliptic curves known as quadratic twists. Here’s an example: the elliptic curve cy2 = x3 − x, where c is some constant. By varying the value of c you twist the elliptic curve. The Goldfeld conjecture concerns all the infinitely different curves you get by varying the value of c.
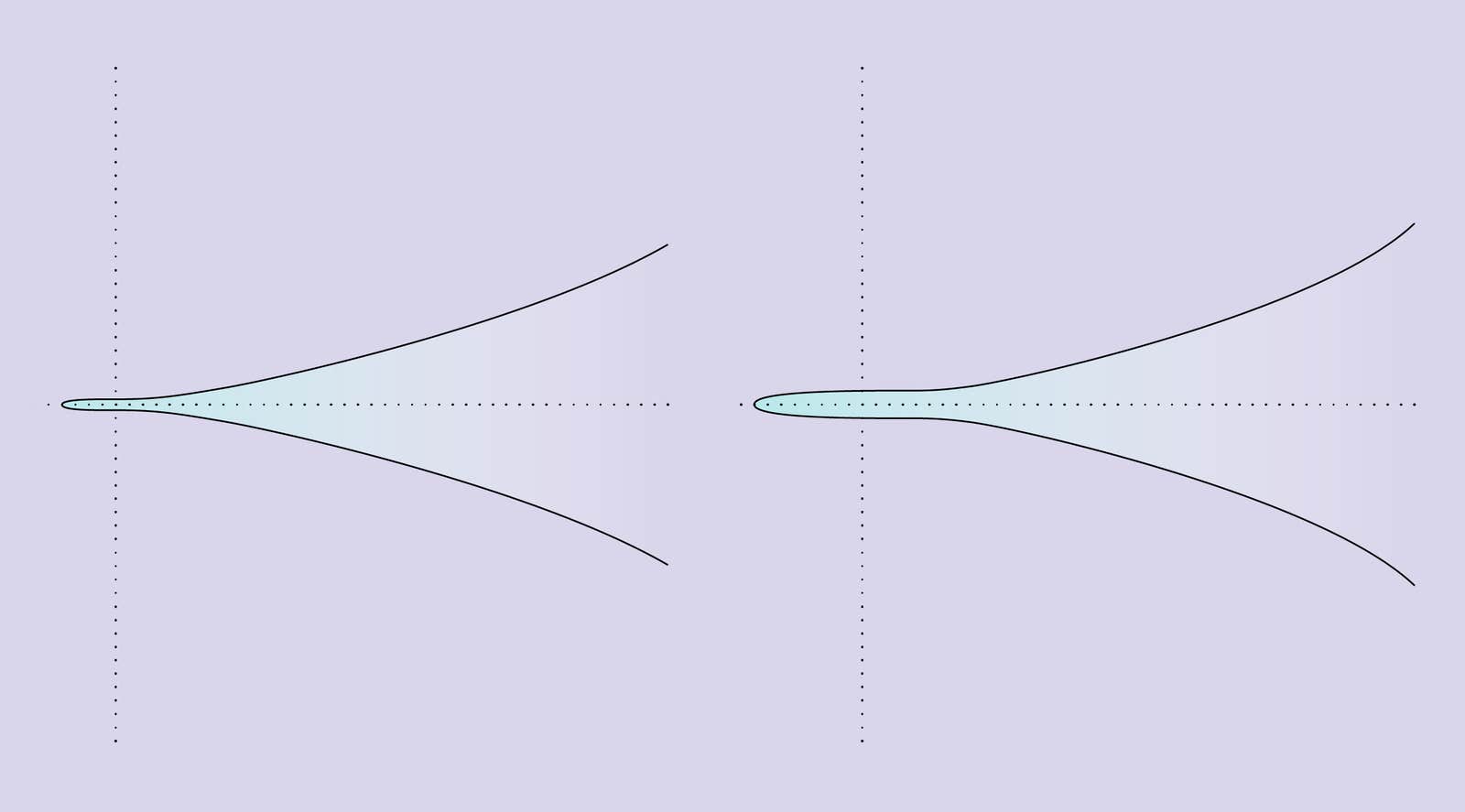
Lead image: Two elliptic curves illustrate how strange the concept of rank can be. The curve on the left, given by y2 = x3 + 1, has only five rational points and a rank of 0. The curve on the right, given by y2 = x3 + 8, has an infinite number of rational points and a rank of 1. Credit: David Song/Quanta Magazine; Source: Dorian Goldfeld
Get the Nautilus newsletter
Cutting-edge science, unraveled by the very brightest living thinkers.
