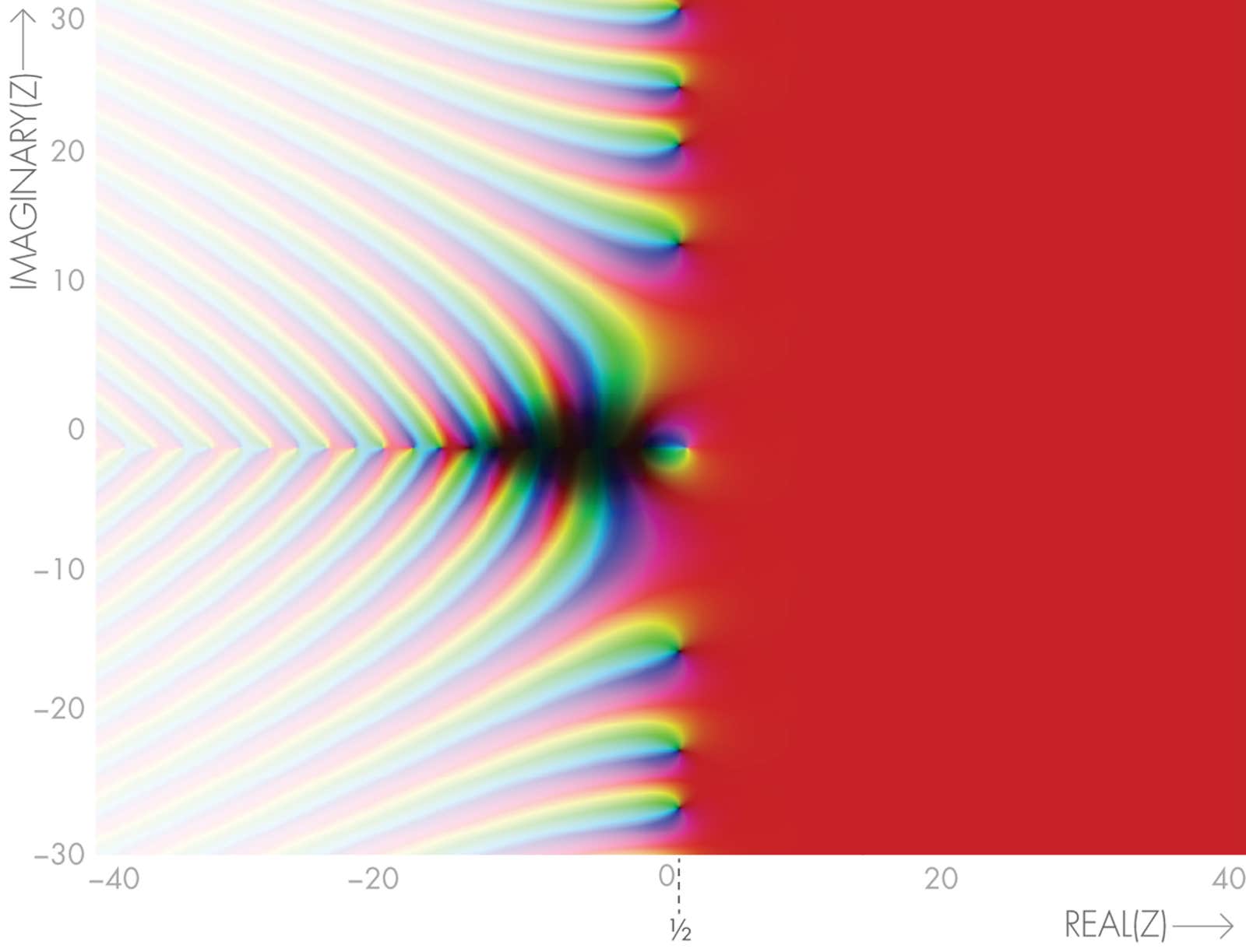
Prime numbers, the indivisible atoms of arithmetic, seem to be strewn haphazardly along the number line, starting with 2, 3, 5, 7, 11, 13, 17 and continuing without pattern ad infinitum. But in 1859, the great German mathematician Bernhard Riemann hypothesized that the spacing of the primes logically follows from other numbers, now known as the “nontrivial zeros” of the Riemann zeta function.
The Riemann zeta function takes inputs that can be complex numbers — meaning they have both “real” and “imaginary” components — and yields other numbers as outputs. For certain complex-valued inputs, the function returns an output of zero; these inputs are the “nontrivial zeros” of the zeta function. Riemann discovered a formula for calculating the number of primes up to any given cutoff by summing over a sequence of these zeros. The formula also gave a way of measuring the fluctuations of the primes around their typical spacing — how much larger or smaller a given prime was when compared with what might be expected.
However, Riemann knew that his formula would be valid only if the zeros of the zeta function satisfied a certain property: Their real parts all had to equal ½. Otherwise the formula made no sense. Riemann calculated the first few nontrivial zeros of the zeta function and confirmed that their real parts were equal to ½. The calculation supported his hypothesis that all zeros had this property, and thus that the spacing of all prime numbers followed from his function. But he noted that “without doubt it would be desirable to have a rigorous proof of this proposition.”
A century and a half later, proving the Riemann hypothesis remains arguably the most important unsolved problem in pure mathematics — one whose solution would fetch a $1 million Millennium Prize from the Clay Mathematics Institute. Conversely, as the number theorist Enrico Bombieri wrote in his description of the problem, “the failure of the Riemann hypothesis would create havoc in the distribution of prime numbers.”
As mathematicians have attacked the hypothesis from every angle, the problem has also migrated to physics. Since the 1940s, intriguing hints have arisen of a connection between the zeros of the zeta function and quantum mechanics. For instance, researchers found that the spacing of the zeros exhibits the same statistical pattern as the spectra of atomic energy levels. In 1999, the mathematical physicists Michael Berry and Jonathan Keating, building on an earlier conjecture of David Hilbert and George Pólya, conjectured that there exists a quantum system (that is, a system with a position and a momentum that are related by Heisenberg’s uncertainty principle) whose energy levels exactly correspond to the nontrivial zeros of the Riemann zeta function. Each of these energy levels, En, corresponds to a zero of the form Zn = ½ + iEn, which has a real part equal to ½ and an imaginary part formed by multiplying En by the imaginary number i.
If such a quantum system existed, this would automatically imply the Riemann hypothesis. The reason is that energy levels of quantum systems are always real numbers (as opposed to imaginary), since energy is a physically measurable quantity. And since the En’s are purely real, they become purely imaginary when multiplied by i in the formula for the corresponding Zn’s. There is never a case where an imaginary part of En is multiplied by i, canceling out its imaginary property and rendering it real, so that it then contributes to the real component of Zn and changes it from ½ to something else. Since energy levels are always real, the real parts of the zeros of the zeta function would always be ½, and the Riemann hypothesis would therefore be true.
Physicists have been searching since 1999 for a quantum system whose energy levels correspond to the zeros of the zeta function. In a paper published on March 30 in Physical Review Letters, Carl Bender of Washington University in St. Louis, Dorje Brody of Brunel University London and Markus Müller of the University of Western Ontario proposed just such a candidate system. But it’s a weird one — and outside experts say it’s too soon to tell whether it will lead to a proof.
Normally, physicists describe quantum systems using highly symmetric mathematical matrices whose solutions, or “eigenvalues,” correspond to the system’s energy levels. The symmetries of these matrices usually guarantee that imaginary numbers cancel out and the eigenvalues are real, so that these matrices make sense as descriptions of physical systems. But for 20 years, Bender and Brody have studied matrix descriptions of quantum systems that relax the usual symmetry requirements and respect a weaker property called parity-time (or PT) symmetry. Following a 2015 conversation with Müller, they discovered that they could write down a PT-symmetric matrix whose eigenvalues correspond to the nontrivial zeros of the Riemann zeta function. “This came as a real surprise to us,” Brody said. However, because the matrix was only PT-symmetric, instead of following the usual stricter symmetries, it isn’t guaranteed to have real eigenvalues — the property that would ensure that corresponding zeros have real parts equal to ½.
The researchers spelled out several arguments for why the eigenvalues of their matrix are probably real, and why, in that case, the Riemann hypothesis is probably correct, but they came short of proving it. “Whether it will be difficult or easy to fill in the missing steps, at this point we cannot speculate,” said Brody. “Further work is needed to get a better feeling as to the scale of difficulty involved.”
Experts say that the new proposal is interesting, but that it’s far from certain whether the authors’ arguments about their unconventional quantum system can be made rigorous. “I would need more time to give a relevant opinion about the significance of their findings as a strategy towards the Riemann hypothesis,” said Paul Bourgade, a mathematician at New York University. In particular, Bourgade said, he would like to explore in more detail how the proposed quantum system compares with one previously proposed by Berry and Keating that has not yielded a concrete proof.
If physicists do someday nail down the quantum interpretation of the zeros of the zeta function, according to Bourgade, this could provide an even more precise handle on the prime numbers than Riemann’s formula does, since matrix eigenvalues follow very well-understood statistical distributions. It would have other implications as well; Berry hopes that a quantum system underlying the primes would serve as a simple model of chaos, demonstrating how chaotic behavior related to the primes can arise out of a nonchaotic quantum system. But we aren’t there yet. Considering how long the Riemann hypothesis has resisted a conclusive proof, Berry urged caution in reading too much into any partial progress. “This latest contribution to the Riemann hypothesis perfectly exemplifies Piet Hein’s dictum,” Berry said: “Problems worthy of attack prove their worth by hitting back.”