Facebook
Twitter
Pocket
Reddit
Email
In February 2020, Quanta reported on a solution to the problem called Ringel’s conjecture. Part of the proof involved using rainbow colorings, special color-coded ways of visualizing information. But the colorful technique has actually been helping mathematicians solve puzzles for a long time, and it figures in an even harder related problem that mathematicians are eyeing next.
Ringel’s conjecture is a problem in combinatorics where you connect dots (vertices) with lines (edges) to form graphs. It predicts that there’s a special relationship between a type of large graph with 2n + 1 vertices and a proportionally smaller type of graph with n + 1 vertices.
To take an example, start with 11 vertices. Connect each vertex to every other vertex to form what’s called a complete graph. Separately, take six vertices and connect them any way you want, so long as you don’t create any closed loops. This creates a “tree.”
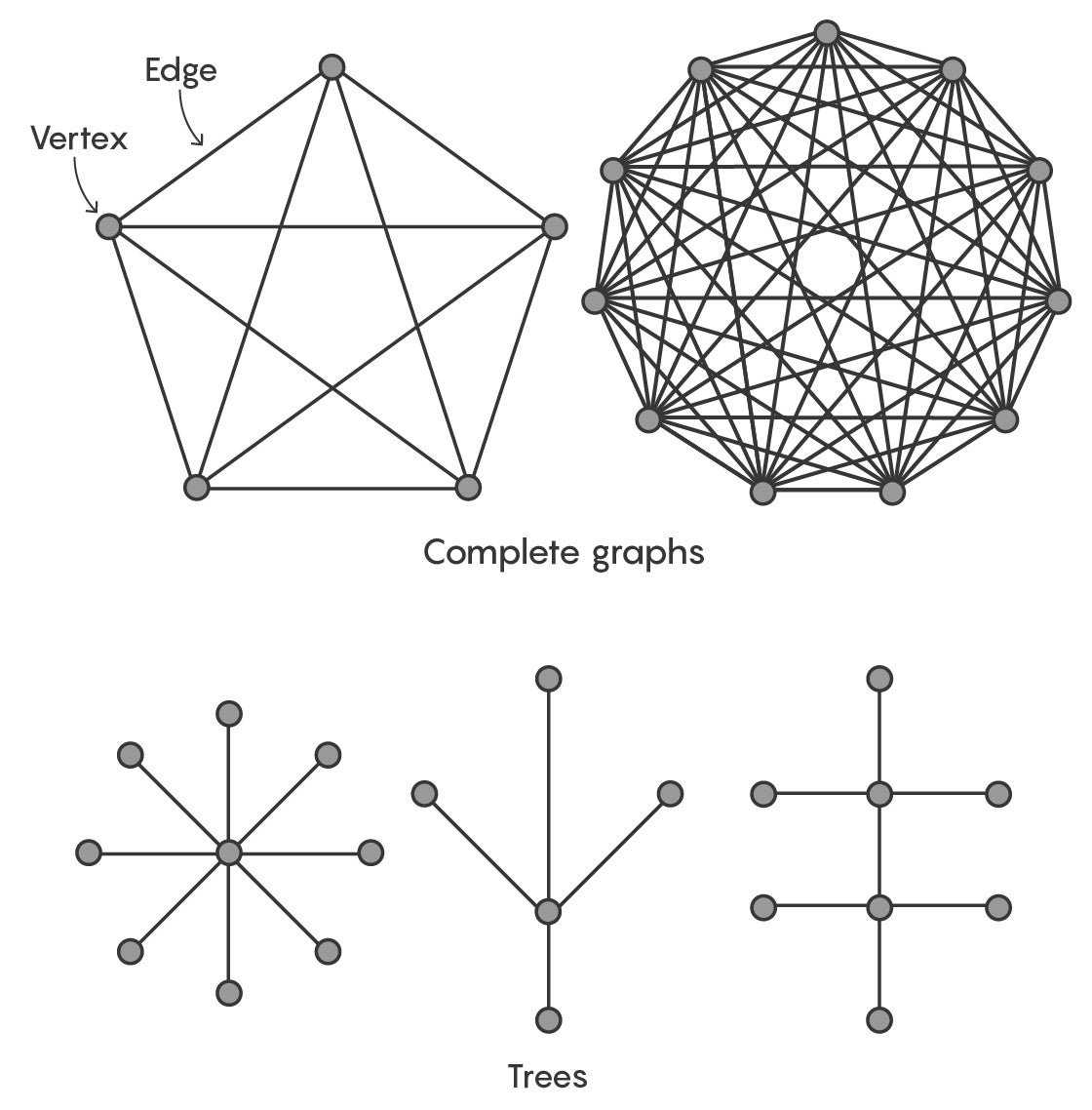
Ringel’s conjecture says that copies of any tree you make can be used to perfectly cover, or tile, the edges of the corresponding complete graph, the same way you could use identical tiles to cover a kitchen floor.
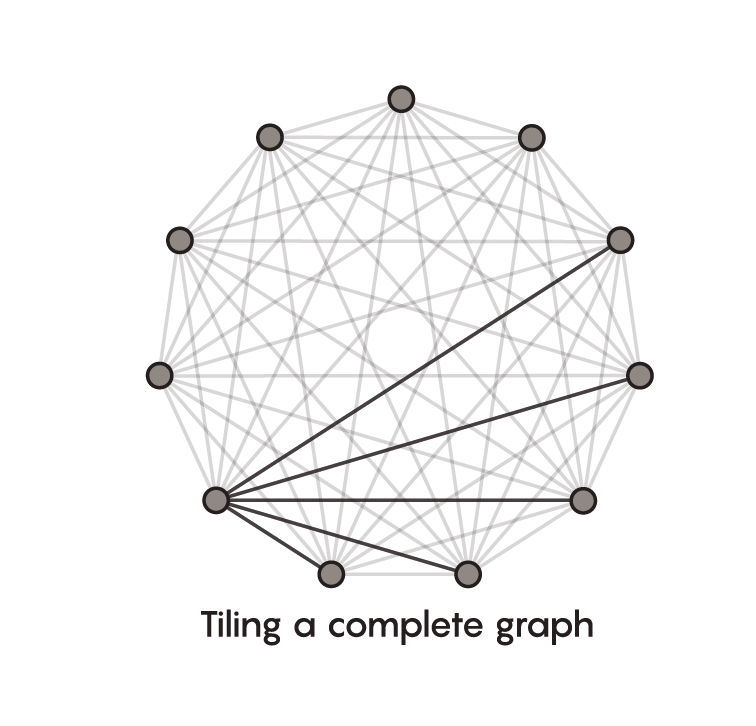
As with your kitchen floor, finding the right placement for the first tile is essential to making the overall tiling effort work. The three mathematicians behind the proof color-coded the edges of the complete graph, based on the distance between vertices, in order to find that placement.
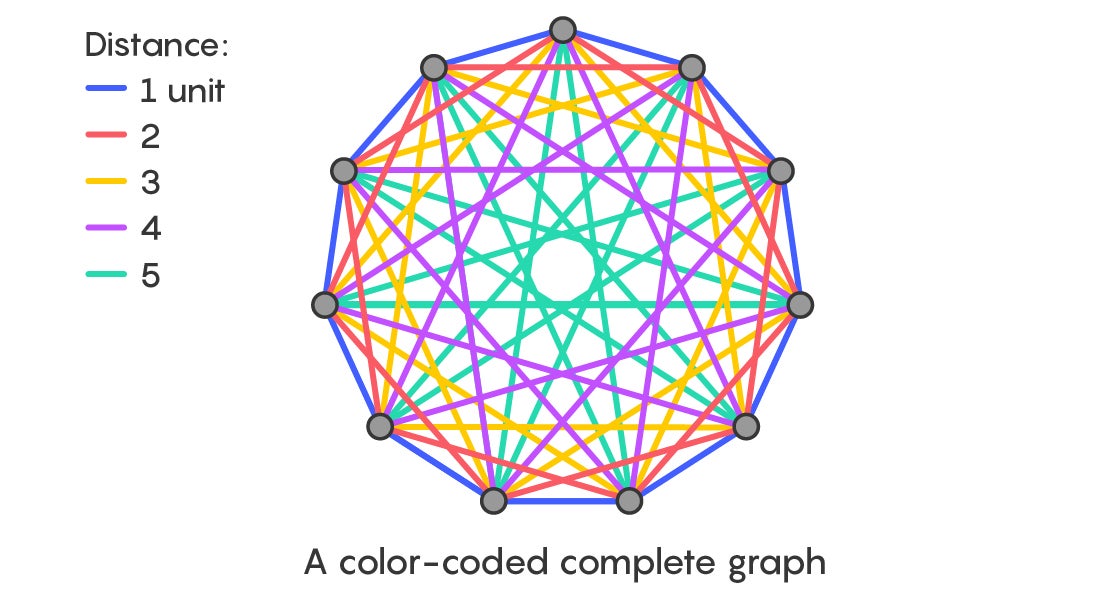
Then they tried to place the tree inside the complete graph so that it covered one edge of each color. By showing that this “rainbow” placement is always possible, they proved that the perfect tiling that Ringel predicted always works out.
This was not the first time that this rainbow technique has come in handy.
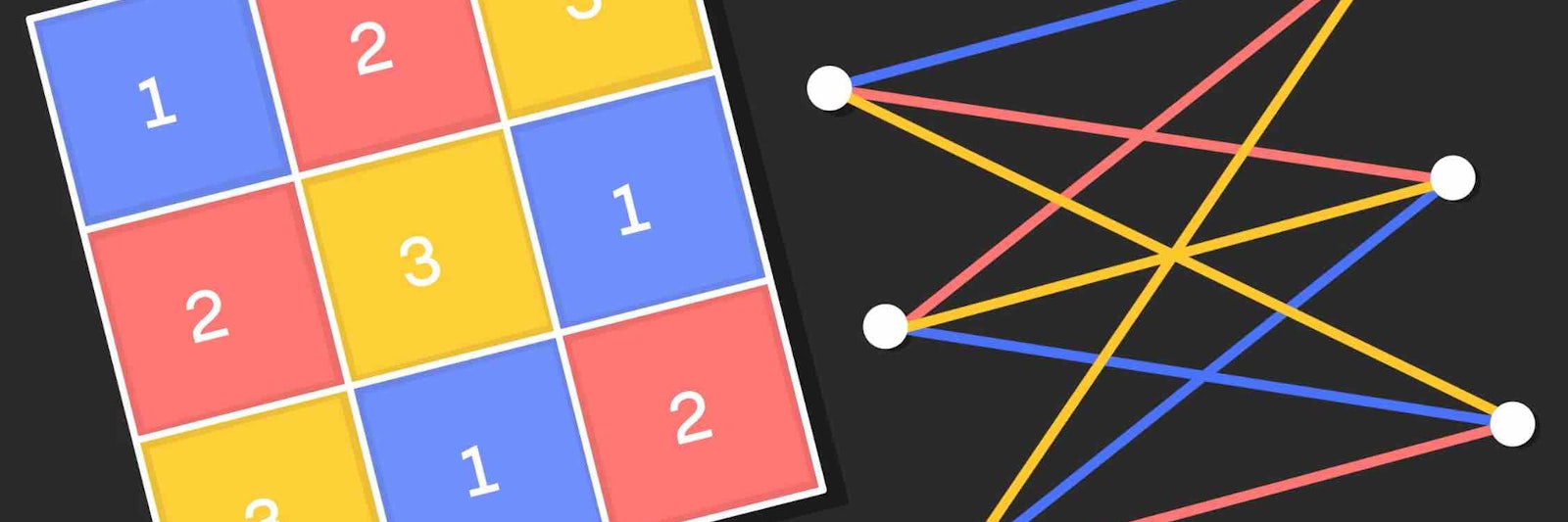
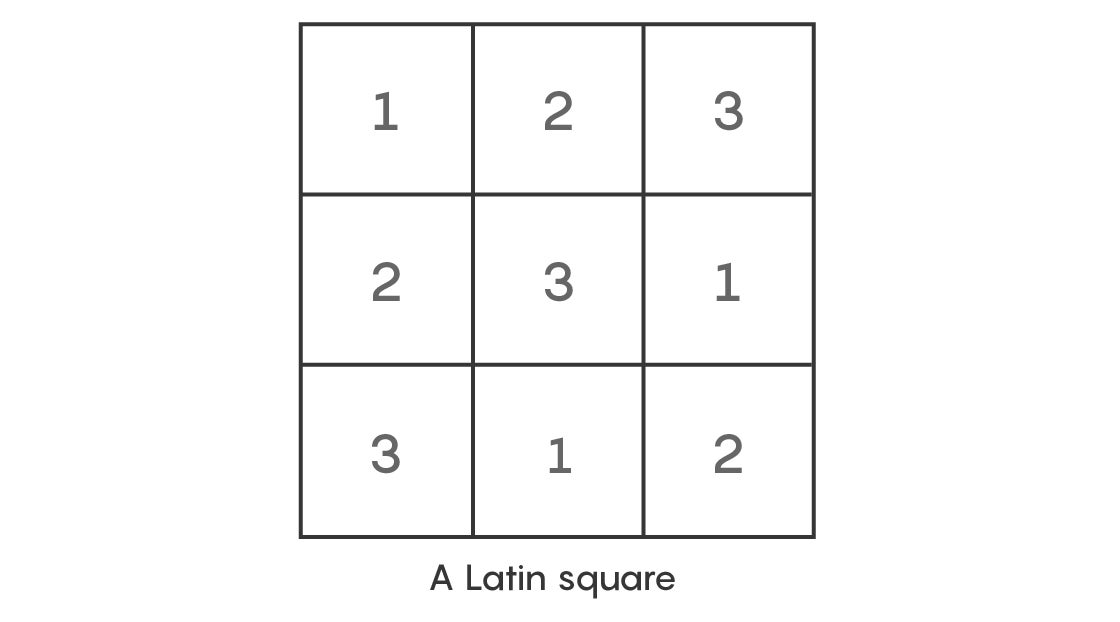
In the 18th century, Leonhard Euler became interested in a kind of baby Sudoku. Take, for example, a 3-by-3 grid. Euler filled it out so that each row and column contained the numbers 1 to 3, with no number repeated. This puzzle is called a Latin square. The patterns and techniques Euler and other mathematicians have uncovered by studying Latin squares have connections to many different areas of mathematics.
Then Euler asked: Is it possible to select three squares—one from each column and one from each row—so that they each contain a different number? Maybe you choose a square in the first row, first column, that contains a 1, a square in the second row, second column, that contains a 3, and a square in the third row, third column, that contains a 2. Now you’ve chosen three squares, each in different rows and different columns, each containing a distinct number: 1, 3, 2. Such a set of squares is called a transversal.
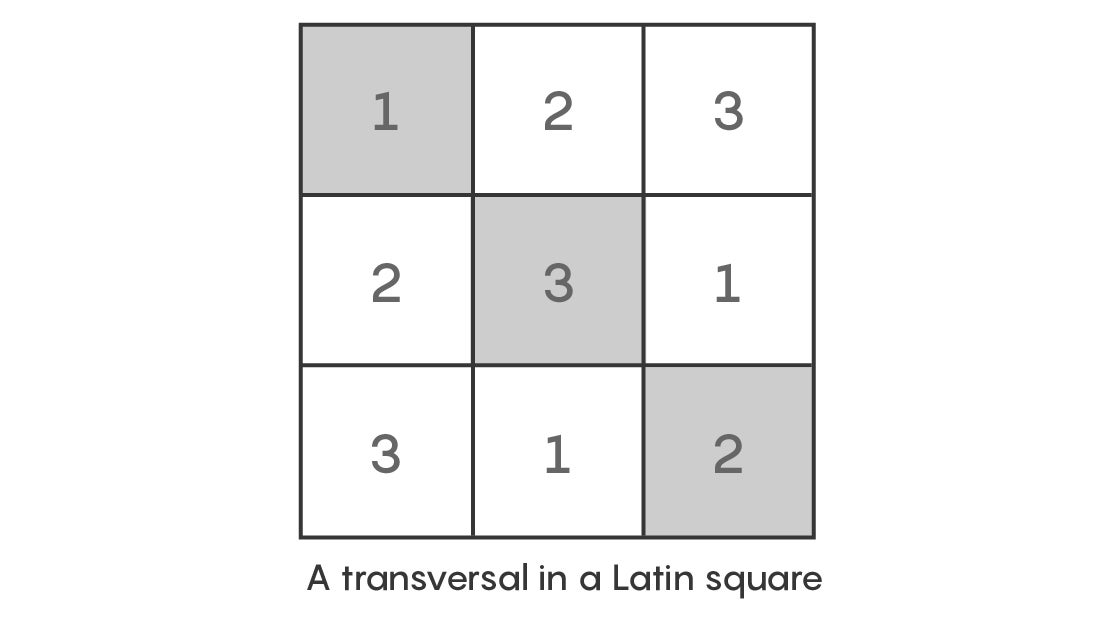
Euler wanted to know if the entire 3-by-3 grid (or square grids of any size) can be perfectly divided into transversal sets, with each set containing one distinct number from each row and column. So in the case of the 3-by-3 square, you’d hope to find three distinct transversal sets that would collectively account for all the squares in the grid.
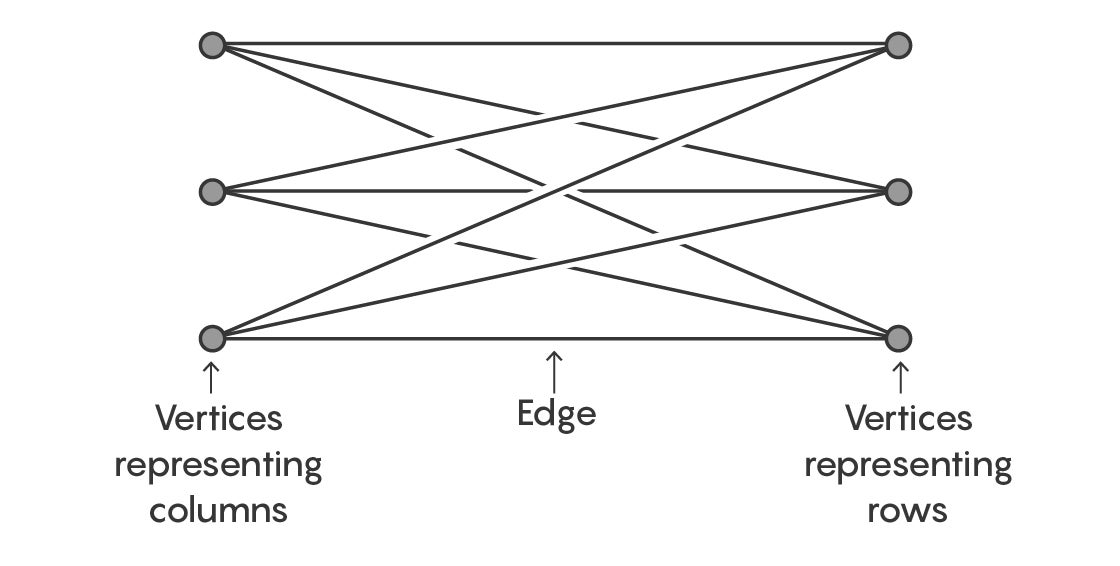
Eventually, mathematicians discovered that one way to investigate this is to turn the square into a graph. To do this, place three vertices on the left side of the page, representing the three columns. Then place three vertices on the right side of the page, representing the rows. Draw edges connecting each vertex on the right with each vertex on the left. Each edge, being the combination of a specific row and column, represents one of the nine boxes. For example, the edge between the top vertex on the right and the top vertex on the left corresponds to the box in the first row and the first column (the top left box in the Latin square).
Now, get out your colored pencils and color-code the edges according to which number in the grid they represent. Let’s say we’ll use blue for any lines representing 1, red for 2, and yellow for 3. If that top left box has a 1 inside, then the edge between the top vertices will be blue.
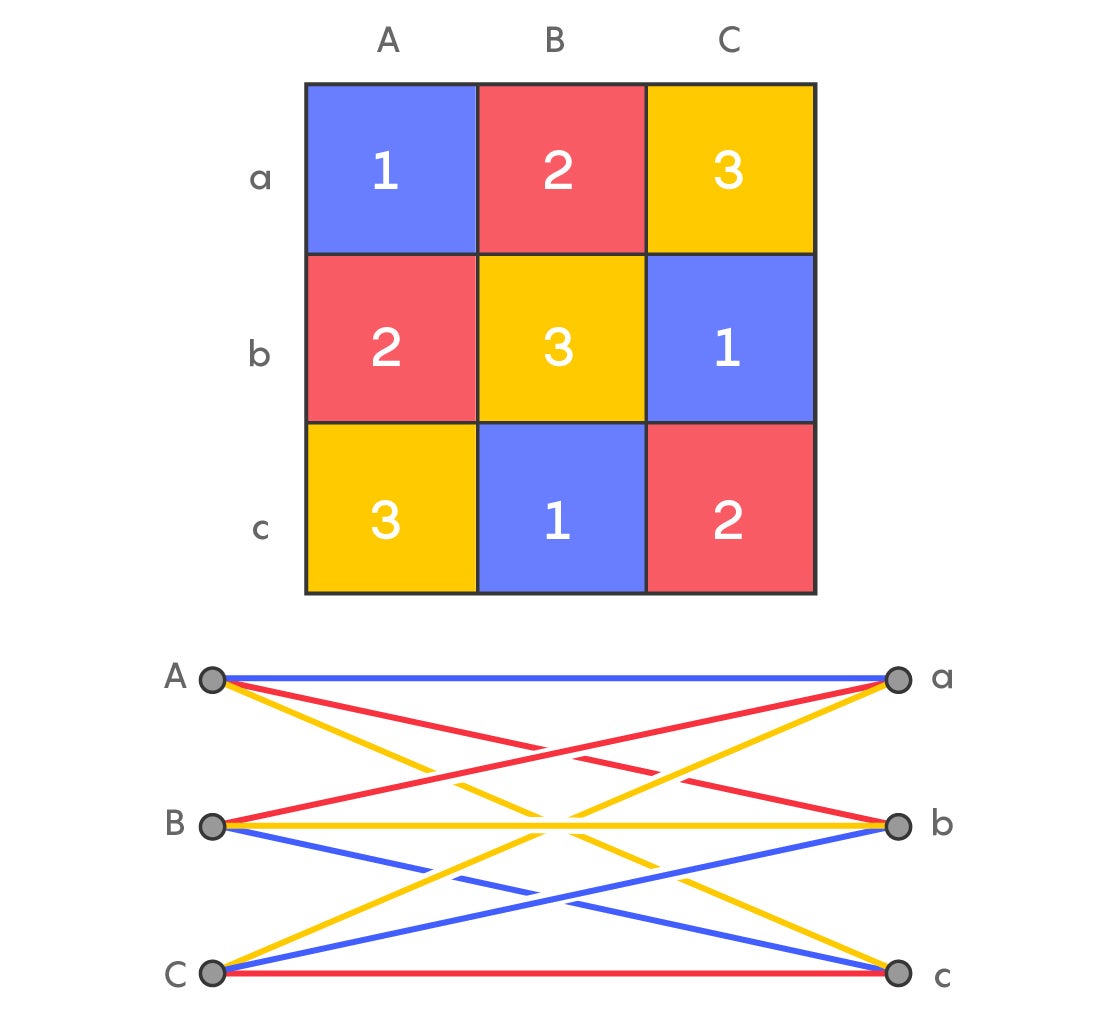
Study the colors of the edges. Is it possible to select three edges, representing all three colors, so that all their starting and ending vertices are different? Such a selection is called a rainbow matching. If you can find it, you know that the corresponding Latin square does indeed contain a transversal. Moreover, if you can find three distinct rainbow matchings, you know the entire Latin square is made up of transversals.
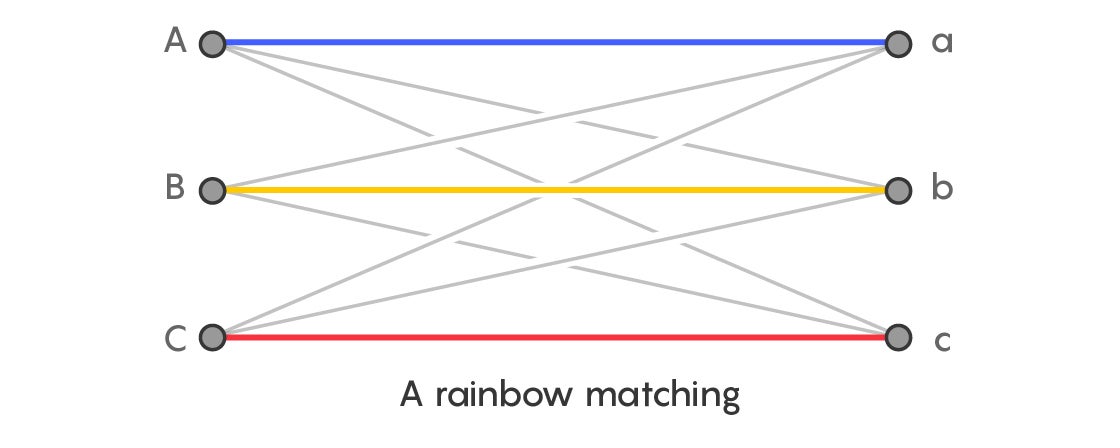
Rainbow colorings helped researchers study problems in the past, and they were key to the new proof of Ringel’s conjecture. They also play a role in an even harder related problem called the graceful labeling conjecture.
To understand the problem, start by drawing six vertices, then connect them to make a tree. Assign a number to each vertex by any means you like. Then label each edge as the difference between the two vertices it connects. So, for example, if an edge connects vertex 6 with vertex 2, label the edge 4.
Your goal is for the edge labels to form a consecutive set of numbers, with no numbers repeated. In this case, 1, 2, 3, 4, 5. If you can do it, the tree has a “graceful labeling.”
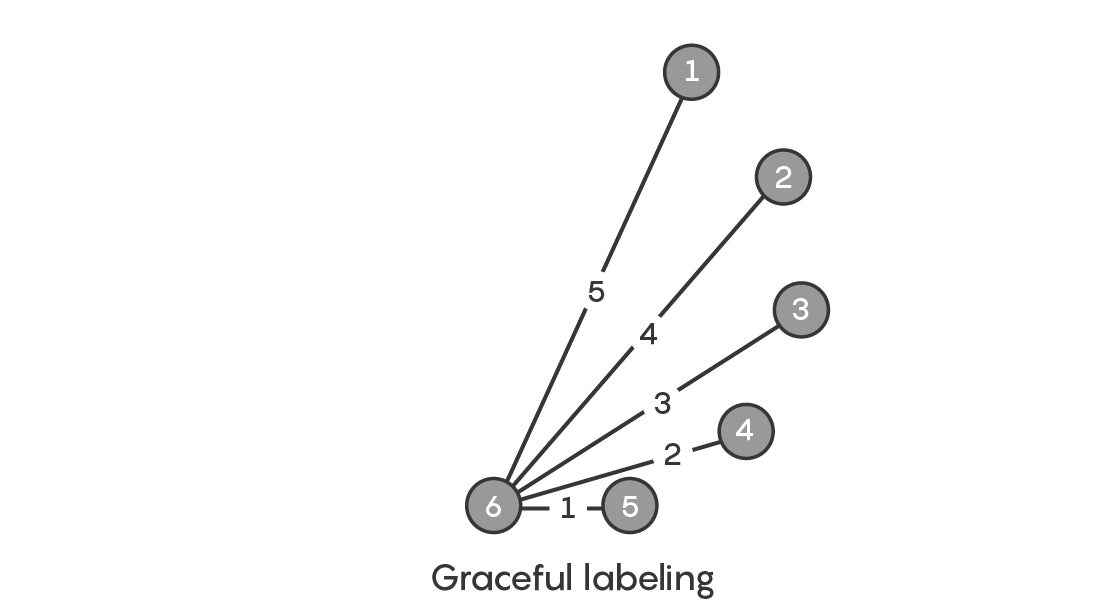
In the 1960s, Gerhard Ringel—the same Ringel behind the conjecture—and Anton Kotzig conjectured that it should be possible to perform this labeling for any tree, no matter the number of edges or the shape.
This graceful labeling conjecture implies Ringel’s conjecture, meaning if the former is true, then Ringel’s conjecture is also true. To see how, let’s return to a gracefully labeled tree with six vertices and a complete graph with 11 vertices. Arrange those 11 vertices in a circle and number them 1 through 11. Now, place a copy of the tree onto the complete graph so that the labels match: Vertex 5 of the tree goes on top of vertex 5 on the complete graph, and so on. This placement, it turns out, is a rainbow copy of the gracefully labeled tree.
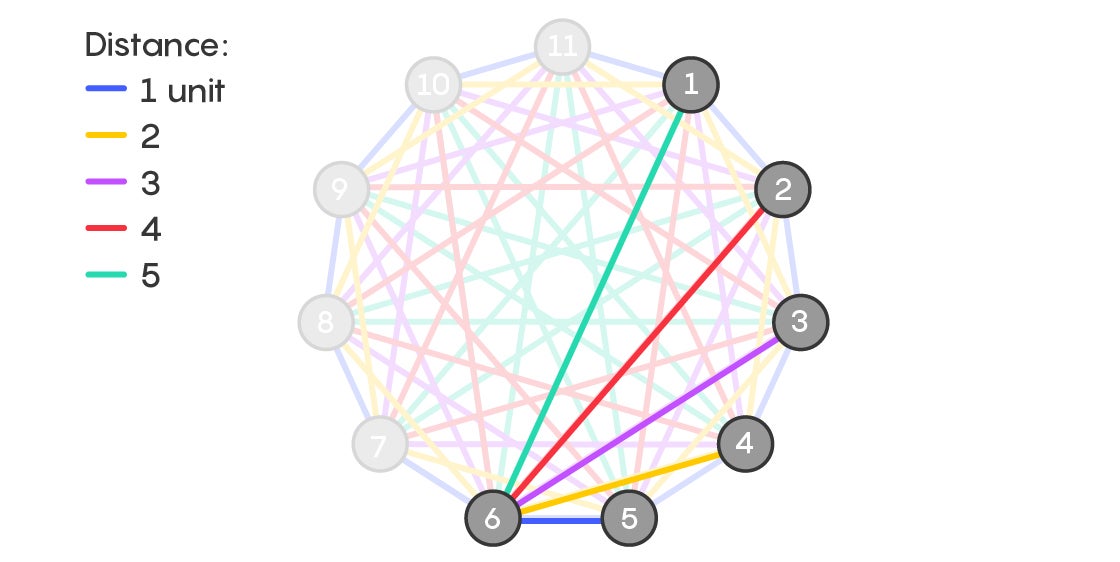
So if you know that trees with n + 1 vertices can always be gracefully labeled, you know they can always be placed inside their corresponding 2n + 1 complete graphs in a way that produces a rainbow copy of the tree. And this placement is the exact right position from which to start Ringel’s tiling process.
“If you find such a graceful labeling, then I can tell you how to find your rainbow copy,” said Benny Sudakov of the Swiss Federal Institute of Technology Zurich, one of three authors of the proof of Ringel’s conjecture.
Of course, mathematicians ended up proving that Ringel’s conjecture is true without needing the graceful labeling conjecture, leaving it an unanswered question.
“Graceful labeling is very appealing and beautiful in its own right, and it is still open,” said Sudakov.
However, the methods that came to fruition in the Ringel proof seem likely to be applicable to graceful labeling—and mathematicians are eager to see just how far they can push them.
Lead image: Color-coding a Latin square and its graph can reveal a lot about them. Credit: Lucy Reading-Ikkanda/Quanta Magazine
Get the Nautilus newsletter
Cutting-edge science, unraveled by the very brightest living thinkers.
