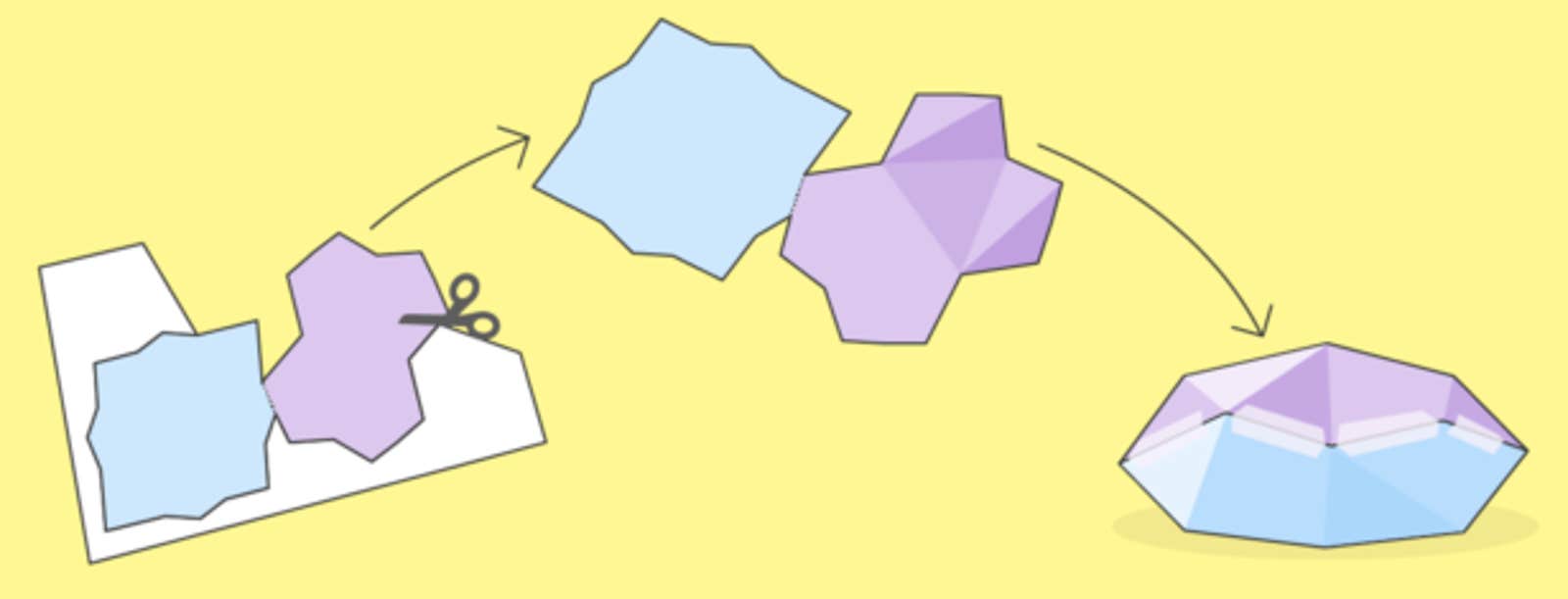
The 20th-century mathematician Aleksandr Aleksandrov proved that for every two-dimensional polygon, there is one unique way of folding it to form a 3-D polyhedron. He also despaired that it appeared to be impossible to come up with a mathematical formula for finding the right folding lines, calling it “a problem whose general solution seems hopeless.”
Absent a mathematical formula, the next best thing is to use paper and tape to experiment with different ways of folding the shapes. That’s what Laura DeMarco and Kathryn Lindsey have done as they’ve tried to understand the properties of a new class of 3-D shapes that arise naturally from polynomial equations. “Kathryn and I spent hours cutting out examples and gluing them ourselves,” explained DeMarco in our new story covering their work.
Now Quanta invites you to construct these shapes. To do so, print out this PDF, which contains instructions and a template. Then try to find the right folding lines as you crease the two-dimensional polygon into a 3-D shape. Send us a picture of your work. The reader who comes closest to finding the correct folding lines will receive a 3-D printed version of one of these exciting new mathematical objects.
How to submit your entry:
1) Post it as a comment on this Facebook post.
2) Tweet it to @QuantaMagazine.
3) Email it to quanta@simonsfoundation.org with the subject line “3-D folding entry.”
Entries will close on January 12 at 11:59pm EST. The winner will be announced on this post, on our Facebook page, and on Twitter.