A few months ago, my aunt sent her colleagues an email with the subject, “Math Problem! What is the answer?” It contained a deceptively simple puzzle:
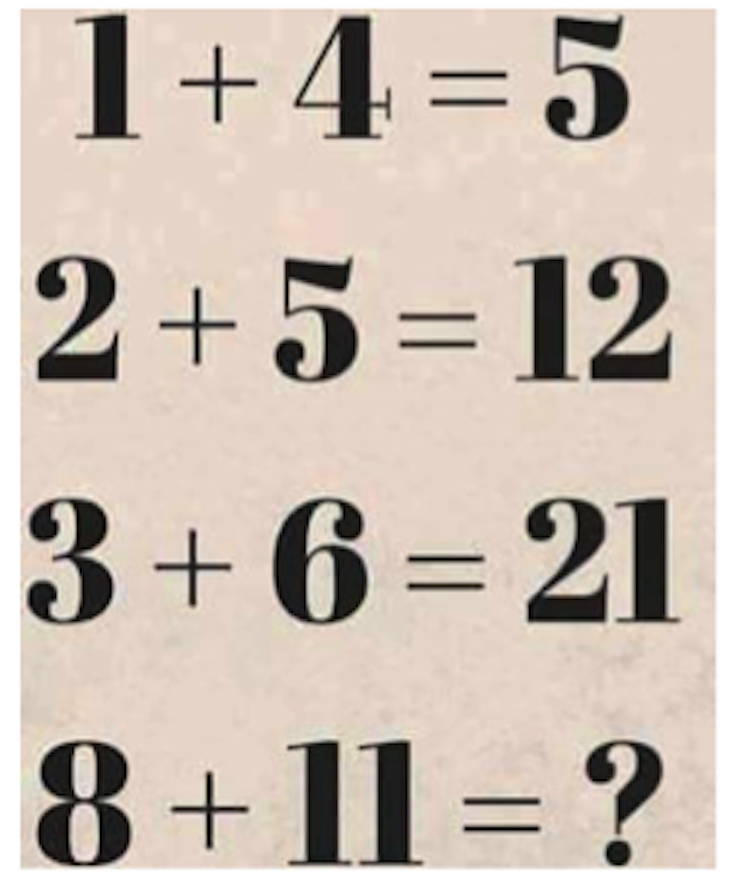
She thought her solution was obvious. Her colleagues, though, were sure their solution was correct—and the two didn’t match. Was the problem with one of their answers, or with the puzzle itself?
My aunt and her colleagues had stumbled across a fundamental problem in machine learning, the study of computers that learn. Almost all of the learning we expect our computers to do—and much of the learning we ourselves do —is about reducing information to underlying patterns, which can then be used to infer the unknown. Her puzzle was no different.
As a human, the challenge is to find any pattern at all. Of course, we have intuitions that limit our guesses. But computers have no such intuitions. From a computer’s standpoint, the difficulty in pattern recognition is one of surplus: with an endless variety of patterns, all technically valid, what makes one “right” and another “wrong?”
The problem only recently became of practical concern. Before the 1990s, AI systems rarely did much learning at all. For example, the chess-playing Deep Thought, predecessor to Deep Blue, didn’t get good at chess by learning from successes and failures. Instead, chess grandmasters and programming wizards carefully crafted rules to teach it which board positions were good or bad. Such extensive hand-tuning was typical of that era’s “expert systems” approach.
To tackle my aunt’s puzzle, the expert systems approach would need a human to squint at the first three rows and spot the following pattern:
1 * (4 + 1) = 5
2 * (5 + 1) = 12
3 * (6 + 1) = 21
The human could then instruct the computer to follow the pattern x * (y + 1) = z. Applying this rule to the final line yields a solution of 96.
Despite expert systems’ early success, the manual labor required to design, tune, and update them became unwieldy. Instead, researchers turned their attention to designing machines that could infer patterns on their own. A program could inspect, say, thousands of photos or market transactions and tease out statistical signals suggesting a face or an impending price spike. This approach quickly came to dominate, and has since powered everything from automated postal sorting to spam filtering to credit card fraud detection.
And yet. With all their successes, these machine learning systems still needed engineers in the loop. Consider again my aunt’s puzzle. We assumed that each line has three relevant components (the three numbers in the line). But there’s a potential fourth element: the result on the previous line. If that attribute of a line—that feature, in machine learning parlance—is in bounds, then another plausible pattern emerges:
0 + 1 + 4 = 5
5 + 2 + 5 = 12
12 + 3 + 6 = 21
By this logic the final answer should be 40.
So which pattern is right? Both, of course—and neither. It all depends on which patterns are allowed. You could also find a pattern by taking the first number times the second number, adding one-fifth of three more than the previous answer, and rounding to the nearest integer. (It’s weird, but it works!) And if we allow features that consider the visual forms of the numbers, perhaps we could come up with some pattern involving strokes and serifs. The pattern matching hinges on the assumptions of the beholder.
Will machines ever learn so well on their own that external guidance becomes a quaint relic?
The same is true in machine learning. Even when machines teach themselves, the preferred patterns are chosen by humans: Should facial recognition software infer explicit if/then rules, or should it treat each feature as an incremental piece of evidence for/against each possible person? And what features should the system attend to? Should it care about individual pixels? Maybe sharp edges between light and dark regions? These choices constrain what patterns the system deems likely or even possible. Finding that perfect combination has become the new job of the machine learning engineer.
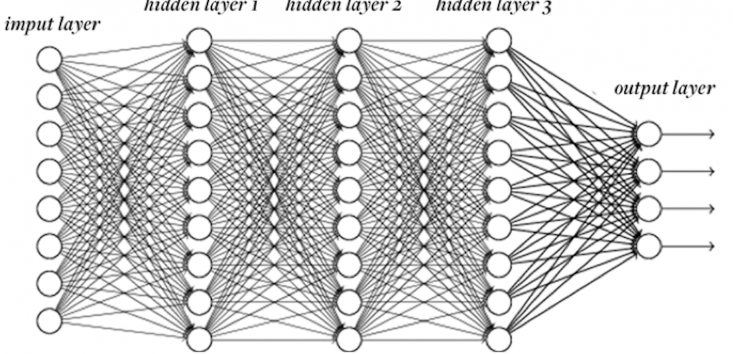
The process of automation didn’t stop there, though. Just as they had once tired of writing rules, engineers began to begrudge designing these features. “Wouldn’t it be nice if the computer could just figure out the features on its own?” And so they designed deep neural networks, a machine learning technique most notable for its ability to infer higher-level features from more basic information. Feed a neural network a bunch of pixels, and it will learn to consider edges, curves, and even textures, all without being explicitly instructed to.
So were the engineers put out of business by the One Algorithm to Rule Them All?
No, not yet. Neural networks still aren’t a perfect fit for all problems. Even in the best cases, they require quite a bit of tweaking. A neural network consists of layers of “neurons,” each performing a calculation on an input and spitting out the result to the next layer. But how many neurons and how many layers should there be? Should each neuron take input from every neuron in the previous layer, or should some neurons be more selective? What transformation should each neuron apply to its inputs to produce its output? And so on.
These questions have constrained efforts to apply neural networks to new problems; a network that’s great at facial recognition is totally inept at automatic translation. Once again, human-chosen design elements implicitly sway the network toward certain patterns and away from others. To a well-informed human, not all patterns are created equal. Engineers aren’t out of a job just yet.
Of course, the logical next step is neural networks that automatically figure out how many neurons to include, what type of connectivity to use, and so forth. Research projects to explore these topics have been underway for years.
How far can it go? Will machines ever learn so well on their own that external guidance becomes a quaint relic? In theory, you could imagine an ideal Universal Learner—one that can decide everything for itself, and always prefers the best pattern for the task at hand.
But in 1996, computer scientist David Wolpert proved that no such learner exists. In his famous “No Free Lunch” theorems, he showed that for every pattern a learner is good at learning, there’s another pattern that same learner would be terrible at picking up. The reason brings us back to my aunt’s puzzle—to the infinite patterns that can match any finite amount of data. Choosing a learning algorithm just means choosing which patterns a machine will be bad at. Maybe all tasks of, say, visual pattern recognition will eventually fall to a single all-encompassing algorithm. But no learning algorithm can be good at learning everything.
This makes machine learning surprisingly akin to the human brain. As smart as we like to think we are, our brains don’t learn perfectly, either. Each part of the brain has been delicately tuned by evolution to spot particular kinds of patterns, whether in what we see, in the language we hear, or in the way physical objects behave. But when it comes to finding patterns in the stock market, we’re just not that good; the machines have us beat by far.
The history of machine learning suggests any number of patterns. But the likeliest one is this: We’ll be teaching machines to teach themselves for many years to come.
Jesse Dunietz, a Ph.D. student in computer science at Carnegie Mellon University, has written for Motherboard and Scientific American Guest Blogs, among others. Follow him on Twitter @jdunietz.