In the field of symplectic geometry, a central issue involves how to count the intersection points of two complicated geometric spaces. This counting question is at the heart of one of the most famous problems in the field, the Arnold conjecture, and it’s also a matter of basic technique: Mathematicians need to know how to make these counts in order to do other kinds of research.
As I describe in my article “A Fight to Fix Geometry’s Foundations,” developing a method for counting these intersection points has been a drawn-out and sometimes contentious process. A reliable, widely understood, error-free approach has presented a challenge for a number of reasons, from the lack of a shared vocabulary when a new field gets started (symplectic geometry only really took off beginning in the 1990s), to the nature of the problem itself: Simply put, it’s hard.
The difficulty lies in the fact that for subtle reasons, it’s not possible to count the intersection points all at once. Instead, mathematicians need to break the space down into “local” regions, count intersection points in each region, and add those together to get the “global” count. Piecing together local counts has proved to be a more delicate and technically demanding task than mathematicians realized at first: If you’re not careful about how you draw your local regions, you could easily omit one intersection point or double-count another.
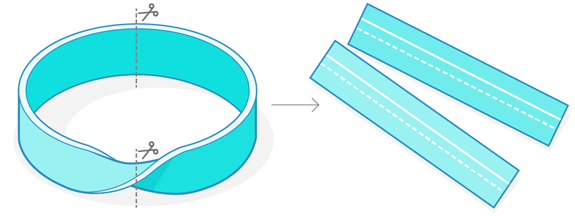
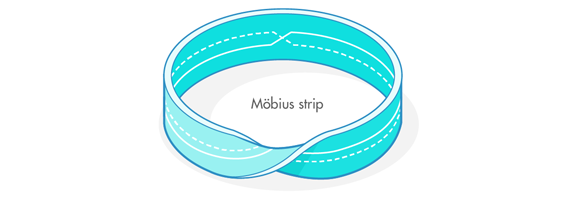
The following illustrations explore the difficulty of the task using a Möbius strip (a two-dimensional circular band with a twist in it). The Möbius strip has two circles passing through its surface. The question is: How many times do the two circles intersect each other? As you’ll see, the answer seems to be one thing when you look at the strip all at once, and another if you’re not careful when you cut the Möbius strip into two pieces.
A Counting Puzzle
Mathematicians want to count intersection points, but certain obstacles prevent them from counting all those points directly. To overcome those obstacles, they divide the manifold into bite-sized “local’’ regions, count the intersections in each and add those together to get a count for the whole manifold.
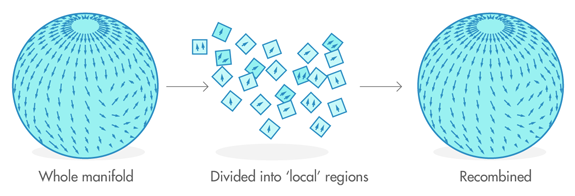
However, if mathematicians are not careful about how they combine counts from local regions, they can easily end up with the wrong count for the whole manifold. The delicacy of adding local counts together is evident in this simple example.
Möbius Rip
Take a Möbius strip. Draw two circles running through it. If you look at the whole Möbius strip, the two circles have to intersect each other at least once: One circle starts above the other, but ends up below it because of the twisting nature of the strip.
Now cut that same Möbius strip into two pieces. The cuts remove the twist in the strip. Draw two circle segments on each piece. Without the twist, it’s easy to draw the circle segments so that they run parallel to each other and never intersect. As a consequence, you might erroneously conclude that the number of intersections on the whole Möbius strip is zero. Mathematicians in symplectic geometry have learned that gluing together “local” pieces to recover a “global” intersection count is a much more complex process than they first imagined.