When particle physicists try to model experiments, they confront an impossible calculation—an infinitely long equation that lies beyond the reach of modern mathematics.
Fortunately, they can generate largely accurate predictions without seeing this arcane math all the way through. By cutting the calculation short, scientists at CERN’s Large Hadron Collider in Europe make forecasts that match events they actually observe when they send subatomic particles barreling toward each other around a nearly 17-mile track.
Unfortunately, the era of agreement between forecast and observation may be ending. As measurements grow more precise, the approximation schemes theorists use to make predictions may not be able to keep up.
“We’re getting close to exhausting what can be done,” said Claude Duhr, a particle physicist at CERN.
But three papers from a group of physicists led by Pierpaolo Mastrolia of the University of Padua in Italy and Sebastian Mizera of the Institute for Advanced Study in Princeton, New Jersey, have revealed an underlying mathematical structure in the equations. The structure provides a new way of collapsing interminable terms into just dozens of essential components. Their method may help bring about new levels of predictive accuracy, which theorists desperately need if they are to move beyond the leading but incomplete model of particle physics.
“They have delivered lots of proof-of-concept results which show that this is a very promising technique,” Duhr said.
There could be a bigger payoff than improved predictions.
The new method skirts the traditional mathematical slog by directly computing “intersection numbers,” which some hope could eventually lead to a more elegant description of the subatomic world.
“This is something that’s not just mathematics,” said Simon Caron-Huot of McGill University, a quantum theorist who is studying the implications of Mastrolia and Mizera’s work. “It’s something that’s deeply baked into quantum field theory.”
An Infinite Loop
When physicists model particle collisions they use a tool called a Feynman diagram, a simple schematic invented by Richard Feynman in the 1940s.
To get a feel for these diagrams, consider a simple particle event: Two quarks streak in, exchange a single gluon as they “collide,” then bounce away on their separate trajectories.
In a Feynman diagram the quarks’ paths are represented by “legs,” which join to form “vertices” when particles interact. Feynman developed rules for turning this cartoon into an equation which calculates the probability that the event actually takes place: You write a specific function for each leg and vertex—generally a fraction involving the particle’s mass and momentum—and multiply everything together. For straightforward scenarios like this one, the calculation might fit on a cocktail napkin.
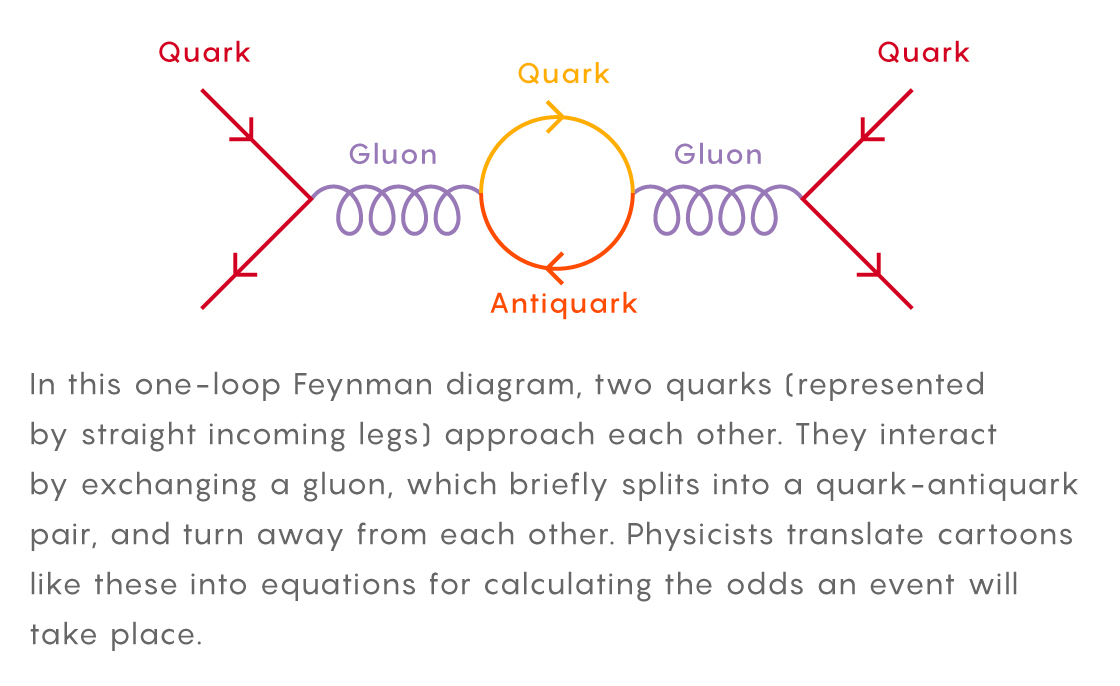
But the golden rule of quantum theory is to consider all possibilities, and exchanging a simple gluon represents just one among a vast landscape of scenarios that could unfold when two quarks collide. The exchanged gluon might momentarily split into a “virtual” quark pair, for instance, before reconstituting itself in a flash. Two quarks enter and two quarks leave, but a lot can happen in the middle. A full accounting, implying a perfect prediction, would demand an infinite number of diagrams. No one expects perfection, but the key to improving a calculation’s precision is getting further along in the infinite line of events.
And that’s where physicists are getting stuck.
Zooming in to that hidden center involves virtual particles—quantum fluctuations that subtly influence each interaction’s outcome. The fleeting existence of the quark pair above, like many virtual events, is represented by a Feynman diagram with a closed “loop.” Loops confound physicists—they’re black boxes that introduce additional layers of infinite scenarios. To tally the possibilities implied by a loop, theorists must turn to a summing operation known as an integral. These integrals take on monstrous proportions in multi-loop Feynman diagrams, which come into play as researchers march down the line and fold in more complicated virtual interactions.
Physicists have algorithms to compute the probabilities of no-loop and one-loop scenarios, but many two-loop collisions bring computers to their knees. This imposes a ceiling on predictive precision—and on how well physicists can understand what quantum theory says.
But there is one small mercy: Physicists don’t need to calculate every last integral in a complicated Feynman diagram because the vast majority can be lumped together.
Thousands of integrals can be reduced to just dozens of “master integrals,” which are weighted and added together. But exactly which integrals can be subsumed under which master integrals is itself a hard computational question. Researchers use computers to essentially guess at millions of relationships and laboriously extract the combinations of integrals that matter.
But with intersection numbers, physicists may have found a way of elegantly plucking out the essential information from a sprawling calculation of Feynman integrals.
A Geometric Fingerprint
Mastrolia and Mizera’s work is rooted in a branch of pure math called algebraic topology, which classifies shapes and spaces. Mathematicians pursue this classification with “cohomology” theories, which allow them to extract algebraic fingerprints from complicated geometric spaces.
“It’s kind of a summary, an algebraic gadget that incorporates the essence of the space you want to study,” said Clément Dupont, a mathematician at the University of Montpellier in France.
Feynman diagrams can be translated into geometric spaces that are amenable to analysis by cohomology. Each point within these spaces might represent one of a multitude of scenarios that could play out when two particles collide.
You might hope, naively, that by taking the cohomology of this space—finding its algebraic structure—you could calculate the weights for the master integrals that support it. But the type of geometric space that characterizes most Feynman diagrams is warped in a way that resists many cohomology calculations.
In 2017, Mizera was struggling to analyze how objects in string theory collide when he stumbled upon tools pioneered by Israel Gelfand and Kazuhiko Aomoto in the 1970s and 1980s as they worked with a type of cohomology called “twisted cohomology.” Later that year Mizera met Mastrolia, who realized that these techniques could work for Feynman diagrams too. In 2019, they published three papers that used this cohomology theory to streamline calculations involving simple particle collisions.
Their method takes a family of related physical scenarios, represents it as a geometric space, and calculates the twisted cohomology of that space. “This twisted cohomology has everything to say about the integrals we are interested in,” Mizera said.
In particular, the twisted cohomology tells them how many master integrals to expect and what their weights should be. The weights emerge as values they call “intersection numbers.” In the end, thousands of integrals shrink to a weighted sum of dozens of master integrals.
The cohomology theories that produce these intersection numbers may do more than just ease a computational burden—they could also point to the physical significance of the most important quantities in the calculation.
For example, when a virtual gluon splits into two virtual quarks, the quarks’ possible lifetimes can vary. In the associated geometric space, each point can stand for a different quark lifetime. When researchers compute the weights, they see that scenarios with the longest-lasting virtual particles—that is, cases in which the particles become essentially real—shape the outcome the most.
“That’s the amazing thing about this method,” said Caron-Huot. “It reconstructs everything starting from just these rare, special events.”
In August 2020, Mizera, Mastrolia and colleagues published another preprint showing that the technique has matured enough to handle real-world two-loop diagrams. A forthcoming paper by Caron-Huot will push the method further, perhaps bringing three-loop diagrams to heel.
If successful, the technique could help usher in the next generation of theoretical predictions. And, a few researchers suspect, it may even foreshadow a new perspective on reality.
Lead image: vchal
Video: The brilliant physicist Richard Feynman devised a system of line drawings that simplified calculations of particle interactions and helped rescue the field of quantum electrodynamics. Directed by Emily Driscoll and animated by Mette Ilene Holmriis for Quanta Magazine.