When representation theory emerged in the late 19th century, many mathematicians questioned its worth. In 1897, the English mathematician William Burnside wrote that he doubted that this unorthodox perspective would yield any new results at all.
“Basically what [Burnside was] saying is that representation theory is useless,” said Geordie Williamson of the University of Sydney in a 2015 lecture.
More than a century since its debut, representation theory has served as a key ingredient in many of the most important discoveries in mathematics. Yet its usefulness is still hard to perceive at first.
“It doesn’t seem immediately clear that this is a reasonable thing to study,” said Emily Norton of the Technical University of Kaiserslautern in Germany.
Representation theory is a way of taking complicated objects and “representing” them with simpler objects. The complicated objects are often collections of mathematical objects—like numbers or symmetries—that stand in a particular structured relationship with each other. These collections are called groups. The simpler objects are arrays of numbers called matrices, the core element of linear algebra. While groups are abstract and often difficult to get a handle on, matrices and linear algebra are elementary.
“Mathematicians basically know everything there is to know about matrices. It’s one of the few subjects of math that’s thoroughly well understood,” said Jared Weinstein of Boston University.
To see how groups can be represented by matrices, it’s worth thinking about each object in turn.
First, we have groups. To take a straightforward example, consider the six symmetries of an equilateral triangle:
- Two rotational symmetries (by 120 and 240 degrees)
- Three reflection symmetries (across lines drawn from each vertex through the midpoint of the opposite side)
- One identity symmetry, in which you do nothing to the triangle at all
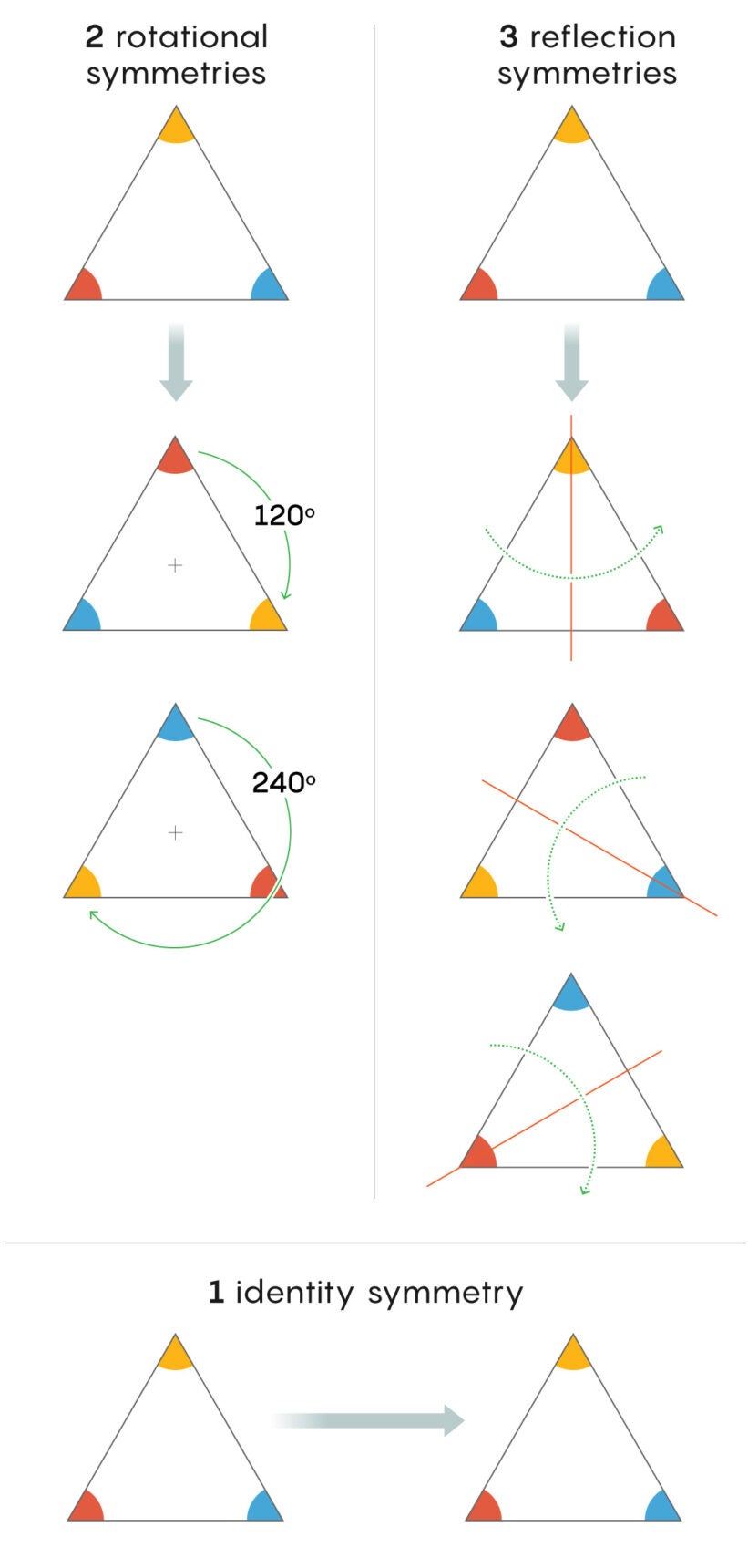
These six symmetries form a closed universe of elements—a group—whose formal name is S3. They form a group because you can apply any number of them to the triangle in a row, in any order, and the end result will be the same as if you’d applied just one symmetry. For example, reflecting the triangle and then rotating it 120 degrees reorders the vertices the same way as if you’d merely performed a different reflection.
“I do something and then something else. The important thing is the result is still a symmetry of the triangle,” Norton said.
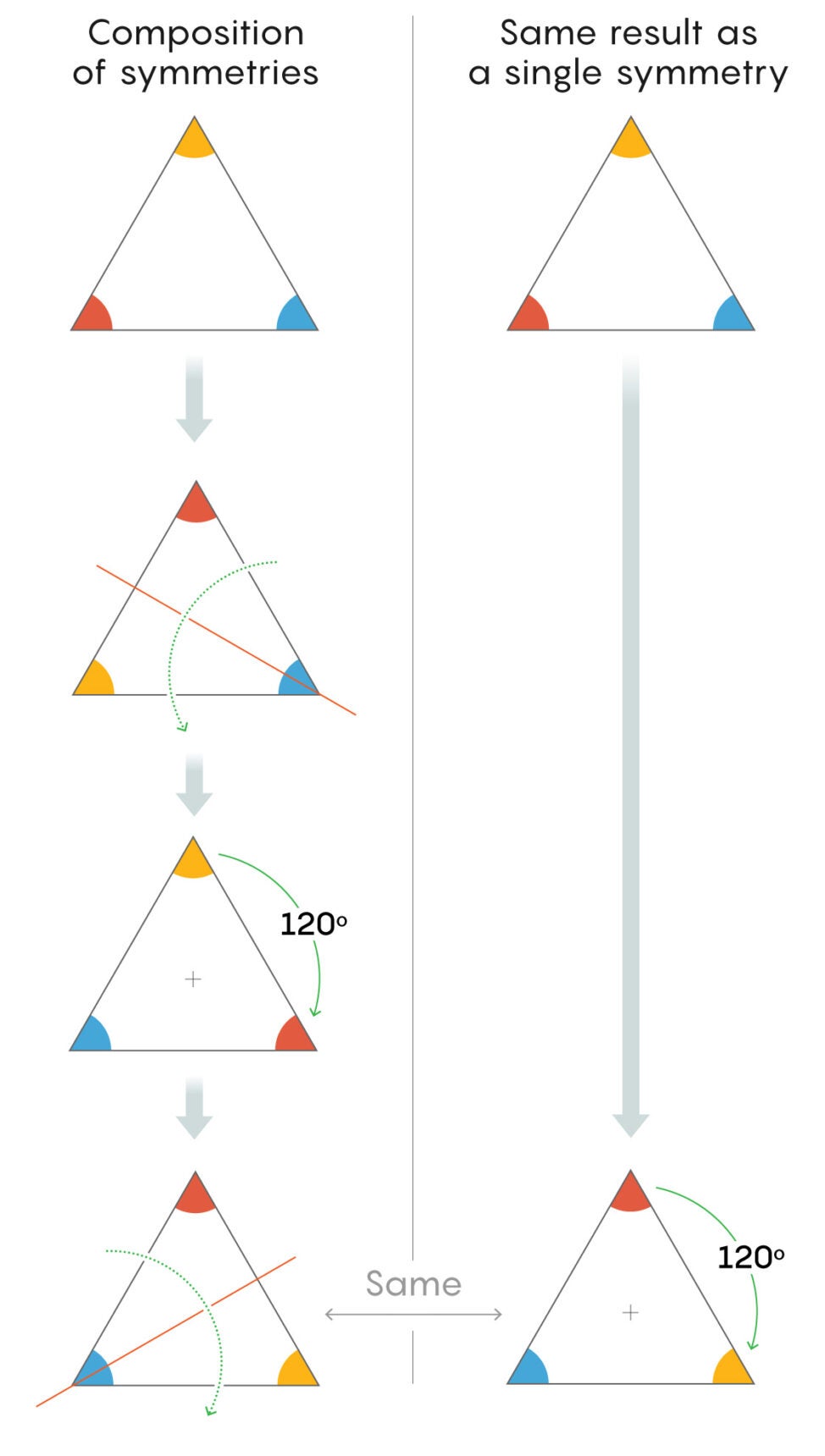
Mathematicians refer to the combination of two symmetries as a composition: One action from the group (a reflection) composed with another (a rotation) yields a third (a different reflection). You can consider composition an act of multiplication, as mathematicians do.
“We like to think of our operations as multiplications even though I’m not multiplying numbers; I’m multiplying transformations,” Norton said.
This is easiest to see if you consider the non-zero real numbers, which also form a group. The real numbers have an identity element—the number 1. Any real number composed with, or multiplied by, 1 remains unchanged. You can also multiply any combination of real numbers, in any order you want, and the product is always also a real number. Mathematicians say the group of real numbers is “closed” under multiplication, meaning that you never leave the group just by multiplying elements.
Since their discovery in the 1830s, groups have become one of the most important objects in mathematics. They encode information about prime numbers, geometric spaces and nearly all the things mathematicians care about most. Solving an important problem often turns on understanding the particular group it’s related to. But most groups are far more difficult to understand than the symmetry group of an equilateral triangle. Instead of six elements, “Lie groups,” for example, contain infinitely many.
“Sometimes groups get pretty damn complicated,” Weinstein said.
That brings us to representation theory, which converts the sometimes mysterious world of groups into the well-trammeled territory of linear algebra.
Linear algebra is the study of simple transformations performed on objects called vectors, which are effectively directed line segments. These objects are defined by coordinates, which can be displayed in the form of a matrix, an array of numbers.
The transformations occur when another matrix is applied to the vector. For example, applying the matrix
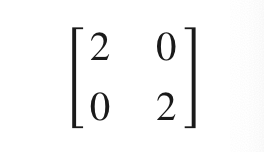
to a given vector stretches it out by a factor of two. This is an example of a “linear” transformation.
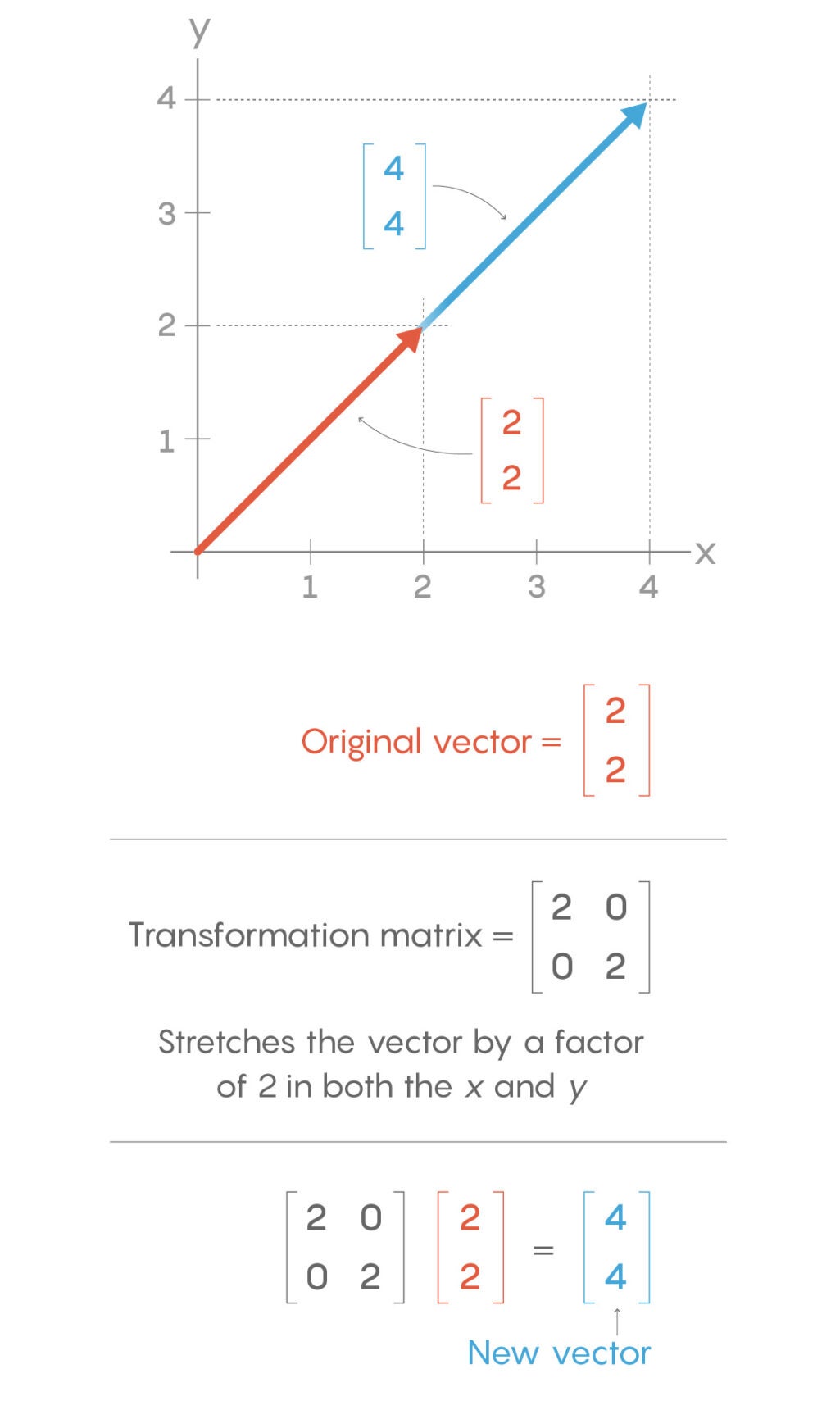
Other matrices perform different kinds of linear transformations, such as reflections, rotations and shears. There is also an “identity” matrix that leaves a vector unchanged (just as the identity symmetry leaves the triangle unchanged and the number 1 leaves other real numbers unchanged):
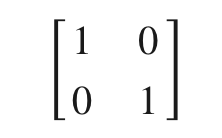
Linear algebra specifies the arithmetic behind those transformations. Matrices can be multiplied, added and subtracted as easily as we perform those operations on regular numbers.
Representation theory creates a bridge between group theory and linear algebra by assigning a matrix to each element in a group, according to certain rules. For example, the identity element in the group must be assigned the identity matrix. The assignments must also respect the relationships between the elements in the group. If a reflection multiplied by a given rotation equals a second reflection, then the matrix assigned to the first reflection multiplied by the matrix assigned to the rotation must equal the matrix assigned to the second reflection. A collection of matrices that respect these requirements is called a representation of a group.
“It doesn’t seem immediately clear that this is a reasonable thing to study,” says Emily Norton of Technical University of Kaiserslautern.
A representation provides a simplified picture of a group, just as a grayscale photo can serve as a low-cost imitation of the original color image. Put another way, it “remembers” some basic but essential information about the group while forgetting the rest. Mathematicians aim to avoid grappling with the full complexity of a group; instead they gain a sense of its properties by looking at how it behaves when converted into the stripped-down format of linear transformations.
“We don’t have to look at the group at once,” Norton said. “We can look at a representation that’s smaller and still understand something about our group.”
A group can almost always be represented in multiple ways. S3, for example, has three distinct representations when real numbers are used to fill in the matrices: the trivial representation, the reflection representation and the sign representation.
Mathematicians collate the representations of a given group into a table—called a character table—that summarizes information about the group. The rows refer to each of the different representations, and the columns refer to important matrices within that representation: the matrix assigned to the identity element in the group, and the matrices assigned to the “generating” elements in the group that, together, give rise to all other elements. The entries of the table are a value called the “trace” of each matrix, calculated by summing the diagonal entries from the upper left of the matrix to the lower right. Below is the character table for the three representations of S3.
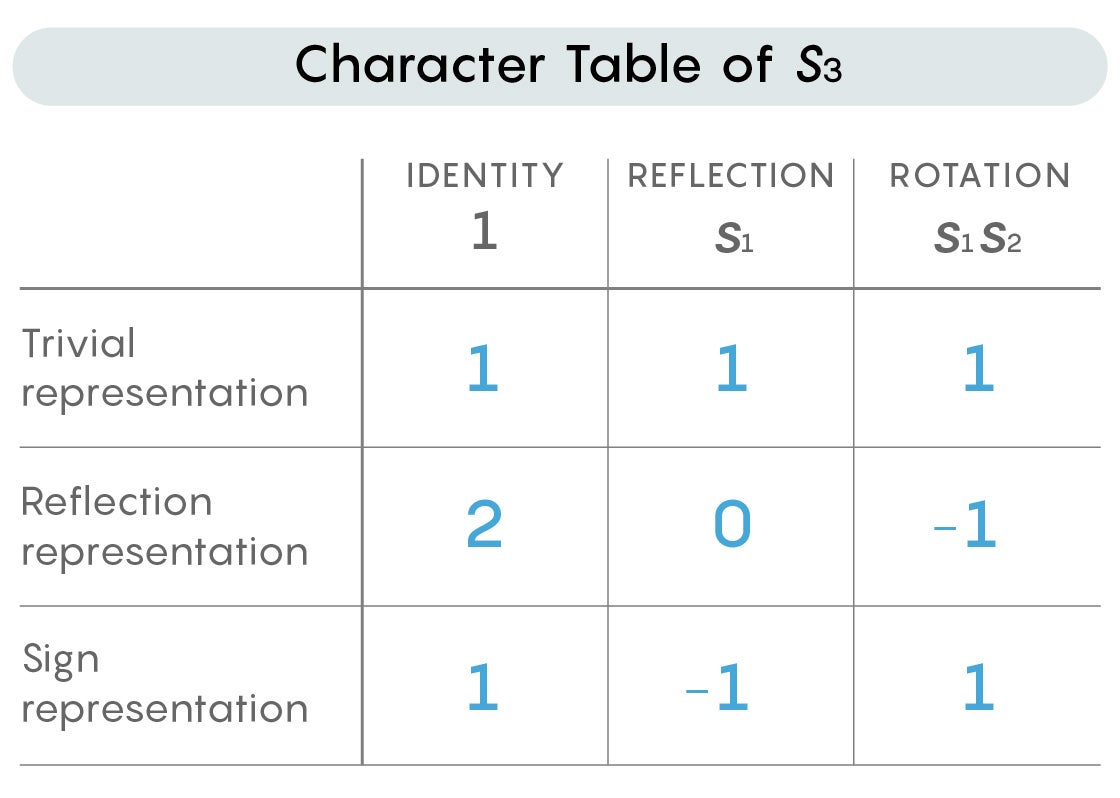
The character table provides a simplified picture of the group. Each representation within it provides slightly different information. Mathematicians combine the various perspectives provided by the representations into an overall impression of the group.
“You have a lot of different representations, which remember different things, and when you put all that information together you have this kaleidoscopic picture of your group in some sense,” Norton said.
The character table above is instantly recognizable to mathematicians as the one for S3. But sometimes the same character table can represent multiple groups—a degree of ambiguity that’s inevitable when you’re dealing with simplifications.
In those ambiguous cases, mathematicians have additional tools at their disposal. One is to change the number system in which they create the representation. The representation of S3 above involves matrices with real-number entries, but you could also use complex number entries (where each number has a real part and an imaginary part). In fact, most of representation theory does.
“Sometimes groups get pretty damn complicated,” says Jared Weinstein at Boston University.
Some of the most fruitful representations involve neither real numbers nor complex numbers. Instead, they use matrices with entries taken from miniature, or “modular,” number systems. This is the world of clock arithmetic, in which 7 + 6 wraps around the 12-hour clock to equal 1. Two groups that have the same character table with real-number representations might have different character tables with modular representations, allowing you to tell them apart.
Today, representation theory is a central tool in many mathematical fields: algebra, topology, geometry, mathematical physics and number theory—including the sweeping Langlands program.
“This philosophy of representation theory has gone on to gobble vast tracts of mathematics in the second half of the 20th century,” Williamson told me in an interview.
Representation theory—and modular representations in particular—played an important role in Andrew Wiles’ landmark 1994 proof of Fermat’s Last Theorem. The problem was about whether whole-number solutions exist for equations of the form an + bn = cn. Wiles proved that no such solutions exist when n is greater than 2. Roughly, he argued that solutions, if they existed, would lead to a group (or “elliptic curve”) with very unusual properties. These properties were so unusual that it seemed possible to show that this object could not exist. However, directly proving its nonexistence was too difficult. Instead, Wiles worked with a family of modular representations that would have been attached to the group if it existed. He proved that this family of modular representations cannot exist, which meant that the group (or elliptic curve) cannot exist, which means that the solutions do not exist either.
Which in turn means that about 100 years after William Burnside dismissed representation theory as useless, it was a critical component in arguably the most celebrated proof of the 20th century.
“I couldn’t conceive of a proof of Fermat’s Last Theorem that doesn’t involve representation theory somewhere,” Weinstein said.
Correction: June 10, 2020
A previous version of this article didn’t specify that the real numbers only form a group under multiplication when you exclude zero. The article has been revised accordingly.
Lead image: Mathematicians can better understand aspects of complicated objects, such as the Lie group visualized here, by representing them with simpler concepts. Credit: Jgmoxness