Gryffindor and Slytherin are about to play their annual badminton match. The best players from each house are supposed to face off on court one, the second best on court two, and so on.
Slytherin’s coach knows that Gryffindor will put their players on the right courts, in order of their skill, because Gryffindors are honest. It’s up to him to teach them the error of their ways. After all, honesty is nothing but a wasted opportunity to cheat.
By strategically putting his players in a different order, can he increase the number of games his team is expected to win? If so, what is the best order to put Slytherin’s players in?
A college friend of mine named Howard Stern (yes, his real name; no, not that Howard Stern) came up with this puzzle in 1980, when he was a graduate student at M.I.T. He worked on it awhile but didn’t completely solve it. Ever since then, he has asked mathematicians about it whenever he got the chance, and never found one who knew the answer. Finally, in 2012, he emailed the question to me. (The Hogwarts theme wasn’t there 33 years ago—that’s my embellishment.)
The earliest reference to Howard’s problem that I have found was a 1983 paper, written by three operations researchers named Arjang Assad, Bruce Golden, and James Yee. It’s no surprise that operations researchers came up with it first: Operations research (“OR” for short) is the science of not wasting resources. In this problem, the resources are the skills of Slytherin’s badminton players, and the challenge is to distribute them in a way that maximizes the expected number of games won.
The first thing to notice about Howard’s problem—or the cheating-coach problem, as I like to call it—is that it’s not quite a mathematical problem yet. You might call it a proto-problem. Real-world problems are often like that; before mathematicians can get the right answer, or any answer, they first have to figure out what is the right question. This usually requires them to make a few assumptions and define a few terms.
In their paper, Assad, Golden, and Yee assumed that the cheating coach would have perfect scouting information on the opposing team. Thus, for each player on his own team and each player on the opposing team, he would know the probability that his player would win.
Unfortunately, Assad’s group knew too much for their own good. A fast solution algorithm for problems like this (called linear assignment problems), suitable for a computer, was already known in 1983. From the perspective of OR, therefore, the question became uninteresting: You can’t publish papers on problems that everybody knows in principle how to solve. In my opinion, that is why the cheating coach problem has languished since 1983.
For a mathematician, though, a solution algorithm is not the same thing as a solution. The human mind craves understanding and insight, which a computer can provide only to a limited extent. A computer can solve one case at a time, but math is about finding patterns that hold for all cases. By prematurely reducing the problem to a computer algorithm, Assad’s group missed the chance to discover some beautiful mathematics. They didn’t ask the right question. (See “Math as Myth,” by Samuel Arbesman, for a different comparison of elegant math done by humans and computational math done by machines.)
Howard Stern looked at the proto-problem in a completely different way. He insisted that Slytherin’s coach should know nothing about the strength of Gryffindor’s players relative to his own. He should know only the information that Gryffindor’s coach has foolishly given him, by being predictably honest: the true ordering of Gryffindor’s players relative to each other. Howard’s version, in my view, poses a very pure question: What is the cost of the Gryffindor coach’s honesty?
The case where each team has three players is a perfect starting place. Think of rating the players from 1 to 6 (1 being strongest) and then assigning them at random to the two houses. There are twenty ways to do this, each of which is equally likely. For example, there is a one in twenty chance that Slytherin will draw players 2, 4, and 6 while Gryffindor draws 1, 3, and 5. If that happens, cheating will make a very big difference. If Slytherin plays 2-4-6 against 1-3-5, all three Slytherin players will lose. On the other hand, if Slytherin plays 6-2-4 against 1-3-5, then they will win two games. (6 loses to 1, but 2 beats 3 and 4 beats 5.)
This version, in my view, poses a very pure question: What is the cost of the Gryffindor coach’s honesty?
By working through all 20 cases, you can show that the best strategy for Slytherin is to “throw” one game, by putting its worst player on court one, best on court two, and second-best on court three. If it does so, it will win by a score of 1.65 to 1.35 on average. Thus, for Gryffindor, the cost of honesty is 0.3 games. I think a lot of athletes intuitively know this. A friend of mine who competes in senior tennis says that teams will often put their players in the order 3-1-2 if they can get away with it.
If there are four players, Slytherin’s best ordering is 4-1-2-3 (again, throwing one game), and with that order they will win on average by 2.34 to 1.66. The cost of honesty has now grown to 0.68 games. And it gets even worse for Gryffindor if there are more than four players.
For the cheating coach, the best strategy changes slightly as the number of players grows. With three to six players per team, the best strategy is to throw one game. But if there are seven players, he should throw two games rather than one. (The best order is 7-6-1-2-3-4-5.) If there are 13 players, he should throw three.
What is the pattern here? How does the optimal number of games to throw depend on the number of players? Computers can’t answer such a question, and may never be able to. The human brain can, and the answer involves some beautiful and ancient mathematics.
The key to the solution lies in this triangle of numbers:
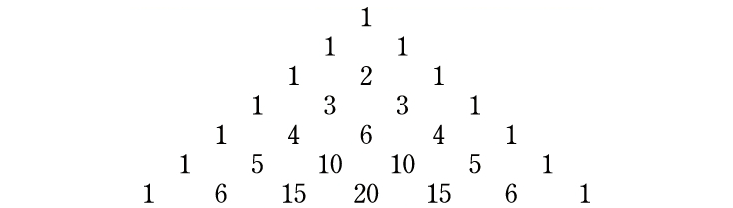
The triangle extends infinitely far down, and it is defined by a simple rule: Below each pair of numbers, you write their sum. For example, below the 10 and the 10 in the bottom row, you write their sum, 10 + 10 = 20.
This arrangement of numbers is called Pascal’s triangle, after the French mathematician Blaise Pascal, who wrote a book about it in 1653. The triangle was actually discovered much earlier (pdf) by Indian, Middle Eastern, and Chinese mathematicians, because it has so many uses. For instance, how did I know there are 20 ways to choose three players from a team of six? I simply looked up the third entry in the sixth row (counting the top row as row zero and the left element in each row as the zero-th entry; see the diagram below for clarification).

So it’s clear that Pascal’s triangle is vaguely connected to the cheating coach problem, but I was totally unprepared for the simple and deep way it provides the answer.
… On the eve of the match, Slytherin’s coach crept, under cover of darkness, into the Hogwarts Mathematics Department. There, on the wall, was a magical, infinitely long scroll with every row of Pascal’s triangle. He scrolled down to a certain row, copied down a few numbers, and added them together. Then he left the room with a sinister smile on his face.
Here is what the coach did. Suppose there are N players on each team; for now, let’s use 7. The recipe is then to look up the 2Nth row in Pascal’s triangle (in this case, the 14th row), which starts as follows: 1, 14, 91, 364, 1001, 2002, 3003, 3432, … The center element in the row is 3432. He adds the other numbers left to right until he gets a total greater than 3432: 1 + 14 + 91 + 364 + 1001 + 2002 = 3473 > 3432. He counts how many numbers are in the sum: six. The correct number of games to throw is the number of players (seven) minus the number he just counted (six) plus one: 7 – 6 + 1 = 2.
To be honest, I have only proved that this is the correct rule if the number of players is greater than 10 million. The proof involves some tricky, but for the most part previously known, estimates from probability theory. Howard has used the computer to verify it when there are 60 or fewer players. Surely the rule also holds for the intermediate range, from 60 to 10 million, but we could use some help from someone with a supercomputer to confirm this.
Working on Howard’s problem has reminded me of something I had forgotten. More than fifteen years had passed since I quit mathematics as a career and started writing. In all that time I had rarely missed it; I remembered mostly the endless frustration of working on problems that wouldn’t budge, that wouldn’t yield their secrets. Howard’s problem was different. I spent more than a hundred hours on it, and never grew tired because it kept throwing me clues, little pats on the back that said, “This idea might work.” It reminded me of the joy of mathematics.
I told you before that the purpose of mathematics is insight, but I think I lied. Even more than that, the reason I do math is the excitement and uncertainty of the chase. There is no joy in applying a computer algorithm, but there is joy in unlocking the delicate clockwork mechanism that makes a good math problem tick. And, in the end, you just might learn something that nobody else in the world knows!
… Oh, and by the way, I really don’t believe that honesty is merely a wasted opportunity to cheat. I said that just for effect. Honest.
Dana Mackenzie is a freelance mathematics and science writer based in Santa Cruz, California. His most recent book is The Universe in Zero Words: The Story of Mathematics as Told Through Equations, published in 2012 by Princeton University Press.






























