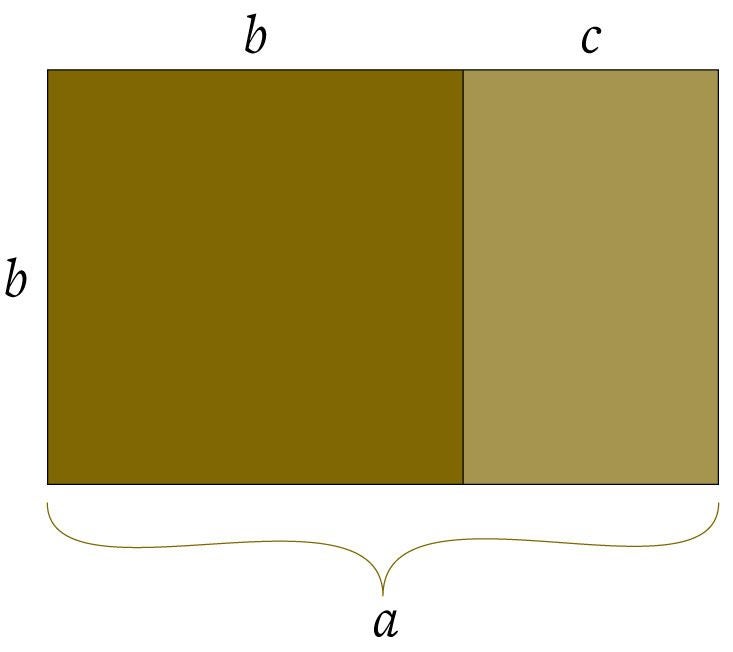
Out of all of the infinite numbers in the world, there are precious few that are given their own letter from the all-too-finite Greek alphabet. The golden ratio, also known by the letter φ, or phi (usually pronounced “fie” in English), is one of those few. An irrational number that begins 1.618…, it describes an important kind of geometrical proportion—specifically, an elegant way to divide a line segment. Imagine we divide a segment (a) into a longer part (b) and a shorter part (c). If the ratio of a to b is the same as b to c, then that single ratio is golden. A rectangle whose sides are lengths a and b is called a golden rectangle, and it’s found in the geometry of a regular pentagon and the Platonic solids, five fundamental 3-D shapes, including the cube. The golden ratio is also tightly connected with the mathematically important Fibonacci sequence: The ratios of successive numbers in the Fibonacci sequence converge to the golden ratio.
So, like fractals, the golden ratio unites different areas of mathematics together. Interestingly, it is also found in many places in nature. For example, evidence of the golden ratio has been detected at the quantum level, where magnetic atoms linked together seem to vibrate at frequencies described by φ. On the macroscopic scale, the Fibonacci sequence and golden ratio describe the natural arrangements of seeds and leaves on many plants. If you examine the packing of seeds on the head of a sunflower, there are a series of clockwise and counterclockwise spirals, which generally appear in successive Fibonacci numbers. The plants are precise enough with their math that one especially robust sunflower reportedly had exactly 233 spirals of seeds one way and 144 the other. In addition, the golden ratio can be converted into an angular version (approximately 137.5 degrees), which specifies the rotational gap between successive sunflower seeds, and also between leaves growing from the stems of many other plants. In both these cases, it is thought that the golden angle allows for the most efficient packing scheme possible, as described by Mario Livio in his book The Golden Ratio. Phi is sometimes called “the most irrational number,” meaning that it is the hardest to approximate with a ratio of rational numbers. This means that by offsetting each leaf by the golden angle from the one below it, the leaves will not line up in stacks, with one on top of another and gaps in between—they instead come in the tightly packed spirals we see in nature.
Phi has also had an interesting role in aesthetics. For centuries, some people have argued that rectangles that have golden proportions are the most pleasing to the human eye. This has inspired artists like Salvador Dali and the architect Le Corbusier to use the golden ratio in their art. Dali’s Sacrament of the Last Supper, for instance, is painted on a large golden-rectangle canvas, and Jesus and his apostles are framed by a somewhat incongruous dodecahedron, one of the Platonic solids. Le Corbusier developed an entire system of measurement called Modulor based on the golden ratio and the human body, which he used in many of his architectural drawings.
For all of the appearances of the golden ratio, there may be even more erroneous sightings of it. The spiral of the nautilus’ shell is often said to fit precisely within a golden rectangle regardless of its size. But that is untrue. Each nautilus shell does maintain the same proportions throughout the animal’s life (that is, it’s a logarithmic spiral), but that proportion is generally not the golden ratio. Many have also claimed that the golden ratio is found in the proportions of various parts of the human body, the shape of the Gutenberg Bible, the Mona Lisa, and the Parthenon. None of these assertions have stood up to skeptical scrutiny, yet these myths stick with us. The mathematician Keith Devlin once gave a talk about the golden ratio, discussing numerous misunderstandings and debunking them, but when a radio station re-broadcast a portion of his lecture, it crucially omitted the fact that the examples were all false. Why does this myth persist? What makes it so resilient and appealing?
While the significance of phi has sometimes been exaggerated, this does not negate a basic truth: The golden ratio, like mathematics in general, is found in many places all around us, and there is amazing power in the mathematical. From the equations describing the ellipses traced by the planets’ orbits, to the inverse square law of gravitation that connects gravity and distance, to the Dirac equation that explains much of physics at everyday energies, mathematics does an impressive job of providing a logical structure to our universe. As far as we know, the universe didn’t need to conform to the kind of equations we write down, but it does. The physicist Eugene Wigner titled a paper on this topic, “The Unreasonable Effectiveness of Mathematics in the Natural Sciences.”
Scientists in the early modern era proved not only the power of math but also of simplicity. Johannes Kepler brought about a revolution in human understanding of the world by proposing that the planets orbited the sun in ellipses. His model was borne out by the fact it predicted the apparent motion of celestial bodies far better than the geocentric Ptolemaic system; using his system, Kepler was the first to realize that Venus would cross between Earth and the sun, making a visible transit. Kepler’s work also became a model for how to do science. He described the motion of the planets with a few simple, very general laws, in contrast to the Ptolemaic system, which depended on a great deal of complexity, including the notorious epicycles—orbits within orbits. Researchers increasingly wanted to see equations, like Kepler’s, that represented the universe’s truths—not fiddly, messy systems crafted by tinkerers. Perhaps the high-water mark of this quest is E=mc2, the shockingly simple relation between mass and energy, and one of the few equations that most people remember. These clean, mathematical explanations are not only preferred; scientists say they are downright beautiful.
But simple, beautiful mathematical explanations can make us greedy. While we wish for all explanations of the world around us to be elegant, science often involves “the slaying of a beautiful hypothesis by an ugly fact,” in the words of biologist Thomas Henry Huxley. Before positing elliptical orbits, Kepler himself succumbed to the desire for beauty when he suggested that the planets’ orbits could be modeled as the Platonic solids nested inside each other. His theory was beautiful, but it was soundly disproved by later observations of the outer planets. In a way, it was almost too beautiful to be right. But beauty cannot be our only metric; beauty must be hampered by reality, if it is to have anything to say about the world around us. Gustav Fechner, a 19th-century psychologist, tried to experimentally prove that people naturally preferred golden rectangles in all kinds of settings, an effort that has not been borne out by subsequent research. It seems he was misled by his “vision of a unified world of thought, spirit and matter, linked together by the mystery of numbers.” This tendency can lead us astray. We see the golden ratio where it doesn’t really exist, and concoct beautiful theories that don’t describe reality.
One thread in psychological research may illustrate both why scientists are seduced by mathematical beauty and why golden ratio myths persist. According to Rolf Reber, a psychologist at the University of Bergen, in Norway, “there is growing empirical evidence that people use a common source for evaluations of both beauty and truth.” The source he refers to is processing fluency, the state of being able to easily parse and understand a situation. Essentially, the more easily we can get a handle on a situation (because it’s mathematically simple, we’ve seen it many times before, it’s symmetrical, etc.), the more likely it is to seem right. For example, researchers have found that processing fluency can affect how people perform something as objective as arithmetic. In one study, Reber showed subjects addition problems represented as patterns of dots with different arrangements. They found that the more ordered and symmetric the arrangements, the more likely they were to be judged as true—whether they were actually true or not. It seems that humans may be wired to believe that famous John Keats line: “Beauty is truth, truth beauty.” Perhaps since the golden ratio has proved interesting in certain ways, it’s more easily understood, and people naturally jump to the conclusion that it should also be used in other cases where it simply is not found.
Processing fluency appears to be a generally useful tool for the problem-solving mind: It gives us a sense of making progress in understanding something and making our way towards a solution. But in science’s search for empirical truth, it may incline researchers to sacrifice some correctness for the sake of beauty. Modern computational methods, however, seem to be shifting the balance back the other way. Take the understanding of human language. Though languages do not adhere to a set of equations, grammar does obey a distinct beauty, with recursive properties that allow for infinite combinations of atomic features like nouns, verbs, and adjectives. A sentence diagrammed—stripped to its logical skeleton—is something magnificent to behold.
But the use of such grammatical models in processing language, such as for translation, simply does not work that well. Language appears to be too complex and quirky for these elegant rules to work when translating a text. Into the gap have stepped numerous statistical approaches from the world of machine learning, where computers ingest huge amounts of translated texts and translate them based on simple algorithms, without ever actually trying to understand what the sentences mean. Out of the chaos comes order—but at a price. The price is a messy intricacy, rather than a simple elegance. Some skeptics, including Noam Chomsky, have even argued (incorrectly) that this doesn’t qualify as science.
Even our aesthetic tastes are, ironically, rather inelegant, as Netflix discovered when it awarded a prize for improvements in its recommendation engine to a team whose solution was cobbled together from a variety of quite different statistic techniques. The contest seemed to show that no simple algorithm could provide a significant improvement in recommendation accuracy; the winners needed to use a messy suite of methods in order to capture and predict our personal and quirky taste in films.
It is good to dream of the simple and the powerfully explanatory. But we are finding out that not all of the world is as easily describable as we might have thought. This is not surprising, as the most easily described features of our universe must necessarily be the simplest. These are then, perhaps, the low-hanging fruit of elegance. We are now left with the more difficult-to-reach fruit, which can only be grasped through a certain amount of complexity and messiness.
In a way, this is frustrating. I want the world to be simple. I want to be able to jot down an equation that articulates the universe.
But that’s okay. The planets don’t nest inside each other like Russian dolls, and the golden ratio isn’t one of the pillars of human aesthetics. The world is messier than that. But it doesn’t mean that it’s not explainable, or even elegant, in its own way. We just need to look a little harder, and prepare to accept truths that don’t glitter like gold.
Samuel Arbesman is a senior scholar at the Ewing Marion Kauffman Foundation and the author of The Half-Life of Facts.






























