Early in their training, many physics students come across the idea of spherical cows. Cows in the real world—even at their most plump and well-fed—are hardly spherical, and this makes it tricky to calculate things like, say, how their volume or surface area scales with their height. But students learn that these numbers are easy to calculate if they assume the cow is a perfect sphere, or in other words, that it has spherical symmetry. The lesson: Hard problems become easier when certain underlying (though approximate) symmetries are enforced.1
The lessons of the spherical cow don’t end with the undergraduate classroom, though. They extend to the very forefront of physics. The theoretical physics community of the 1980s and 1990s was split by debates over the reality of symmetries similar to, but much more complex than, the spherical cow. String theorists argued for a single, unified mathematical description of reality that relied on certain symmetries, but had almost no experimental support. Other physicists argued that the role of a theory was to predict and explain experiment, and not to pursue mathematical structures for their own sake—no matter how beautiful they might be. The warring factions began to reconcile in the last decade with the realization that some of the sophisticated tools that string theorists had built could be applied in unexpected ways to other problems, and could even help make sense of real data.
Late in 2013, the latest chapter in the history of symmetry in physics began to unfold, when two theoretical physicists unveiled a new calculation tool called the “amplituhedron.” The amplituhedron is an exotic, flat-faceted geometric object that lives in an abstract, mathematical space of many dimensions. It can quickly yield answers that have up until now taken hundreds of pages of calculation. Most intriguingly, its power derives not just from making some symmetries apparent, but also from abandoning old symmetries. In doing so, it may point the way to changing how we think about space and time.

Diagrammatic Fables
Beginning in the late 1920s, great architects of quantum theory like Werner Heisenberg, Wolfgang Pauli, and Paul Dirac recognized that physical forces arise from the exchange of certain force-carrying particles. For example, photons—individual particles of light—are the force-carriers of electromagnetism. Charged particles like electrons exert an electromagnetic force on each other by trading photons back and forth. Over the course of the 1930s, physicists figured out ways to approximate the “amplitudes” for such processes, which tell them how likely they are to occur.
In the simplest approximation, two electrons interact with each other by trading a single photon. The resulting approximate calculations are in reasonable agreement with experiments. Yet quantum theory suggests that the electrons could trade any number of photons back and forth: two photons, three photons, 9 million photons, and so on. Each byzantine variation should contribute a modest numerical correction to the overall amplitude, since electrons and photons interact weakly with each other. The problem is that even the next-simplest case—trading two photons instead of one—is ferociously difficult to calculate. One of Heisenberg’s intrepid students attempted such a calculation in 1936; his published equation spilled over several pages.
After World War II, a young Richard Feynman took up the challenge. He began to doodle as he imagined a sequence of events (see The First Feynman Diagram). On the left and right are lines representing electrons traveling through space and time (in the upward direction). They interact with each other by emitting and absorbing a photon, which carries enough oomph—energy and momentum—to change each electron’s motion. The electrons thereby exert a force on each other, pushing each other apart. With this framework, Feynman could easily tackle more complicated interactions between two electrons, sketching, for example, all the ways that two electrons could trade two photons back and forth.
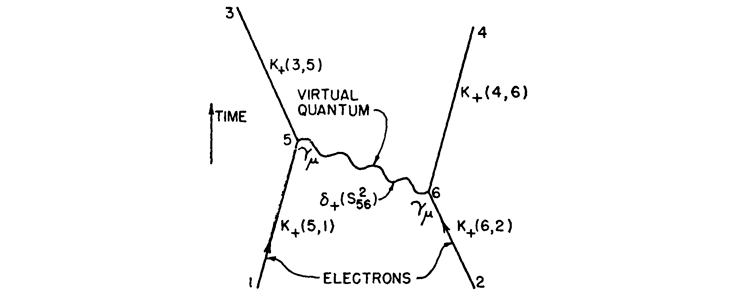
Feynman’s diagrams served as fables, each element geared to convey a specific message. An electron had a certain likelihood of emitting or absorbing a photon, just as a photon had a certain likelihood to travel, unimpeded, from point A to point B. Feynman identified each element of his drawings with a corresponding mathematical expression. With those simple translation rules in hand, he could dispatch in half an hour the kind of calculations that had stymied the world’s best theoretical physicists for decades.
Physicists have since tackled ever more complicated calculations using Feynman diagrams. Toichiro Kinoshita of Cornell University, for example, has spearheaded efforts to calculate the effects of electrons exchanging four photons, a calculation involving nearly 900 distinct Feynman diagrams. The theoretical results match experimental measurements to better than one part in a trillion, by far the most precise agreement between theory and experiment in the history of science. Feynman diagrams in hand, physicists learned to calculate things that few had even dreamed of before the war.2
Symmetries and Improvisations
Feynman had created his diagrams to help calculate interactions among electrons and photons. But soon after he introduced them, physicists began to apply them to a rather different set of interactions: nuclear forces. The transfer wasn’t always easy. For one thing, nuclear particles like pions and other “mesons”2 seemed to interact strongly with each other, quite unlike the weak coupling between electrons and photons. This meant that the more complicated diagrams, with more force-carrying particles in the mix, could no longer be treated as small corrections to the simpler diagrams, as they could with photons and electrons. Instead, these more complicated diagrams were weighted more than simpler diagrams when calculating amplitudes—and there were infinitely many such diagrams to consider. Feynman grew suspicious, writing to Enrico Fermi late in 1951, “Don’t believe any calculation in meson theory which uses a Feynman diagram!”
Despite Feynman’s misgivings, others plowed on. Among the earliest to adopt Feynman diagrams were the young theorists C.N. Yang and Robert Mills, working at the new Brookhaven National Laboratory in Long Island, New York. Brookhaven had one of the most powerful particle accelerators at the time, and Yang and Mills were eager to make sense of the dizzying variety of nuclear particles and interactions that the accelerator revealed.
The amplituhedron approach makes the older, Feynman-diagram tools look as helplessly outdated as room-filling, jerry-built, vacuum-tube computers.
In 1954, Yang and Mills returned to an idea that Heisenberg had floated in the early 1930s: When it comes to nuclear reactions, neutrons and protons appeared to act indistinguishably. They were certainly different particles—protons carried one unit of electric charge, while neutrons had no charge—and yet neutrons and protons seemed to interact with other nuclear particles, such as pions, in a symmetrical way. Exchanging protons for neutrons, and vice versa, appeared to make no impact at all. Physicists had a term for such differences that made no difference: “gauge invariance.”
The young theorists built a new model of nuclear forces by elevating this dimly-glimpsed symmetry into a founding principle. What if all nuclear interactions had to respect the symmetry between neutrons and protons? Such a symmetry could only be upheld, they found, if they included a new type of particle. The sole purpose of the hypothetical “gauge particle”—at least in Yang’s and Mills’ calculations—was to scatter (or bump) off of other nuclear particles in just such a way as to compensate for any possible differences in outcomes involving protons versus neutrons. All those scatterings, meanwhile, meant that the gauge particle would transmit forces: It was the force-carrier of the nuclear force, a cousin to the photon of electromagnetism.
Here was symmetry with a vengeance. Yang and Mills made a leap from Heisenberg’s intuition and scattered experimental evidence to suggest that the neutron-proton symmetry held exactly. To protect that symmetry, they had to dream up a whole new type of matter, which generated the very interactions among nuclear particles that Yang and Mills had set out to try to understand.
By the mid-1970s, particle physicists had pieced together a complicated collection of nuclear forces known as the “Standard Model,” involving several different types of gauge particles. Within a few years, they began to accumulate experimental evidence for “gluons,” the gauge particles that keep quarks bound inside protons, neutrons, and other nuclear particles. Large experimental teams at CERN first detected gauge particles of the “weak nuclear force”—the force that causes nuclear reactions like radioactive decay—in 1983. Once imagined as a mere mathematical device, Yang-Mills gauge particles have become part of our world, physical instantiations of underlying symmetries.
Having established that gauge particles are real, physicists needed to calculate their behavior, including detailed scattering amplitudes. This proved to be difficult. Yang and Mills had made a modest-looking tweak to Feynman’s rules for calculating with his diagrams, allowing direct scattering of gauge particles off each other, as required by their role in protecting gauge symmetries. While this looked simple, it produced enormous headaches. Feynman diagrams now needed to include closed loops formed just from gauge particles, a complication that never arose when applying the diagrams to electron-photon interactions.
Feynman himself demonstrated in 1963 that such closed loops would spoil the very symmetry that the gauge particles had been invented to enforce. So physicists had to insert still more strange mathematical machinery into their calculations, including “ghosts”: fictitious particles whose sole purpose is to chase gauge particles around in certain types of Feynman diagrams, ultimately cancelling out of the calculations when different diagrams are added together. Unlike the gauge particles themselves, the “ghosts” (as their name implies) were not supposed to represent genuine particles. They were a mathematical fiction, a kludge invoked so that Feynman diagrams—a tool invented for other purposes—could be applied to models with Yang-Mills symmetry.
As a result, physicists have doggedly spent the last decades using this work-around, filling blackboards and journal articles with hundreds of Feynman diagrams littered with distinct squiggles for gauge particles and ghosts, wrestling with the fact that the symmetries that Yang and Mills introduced seem to have gummed up the works (see Feynman Zoo).
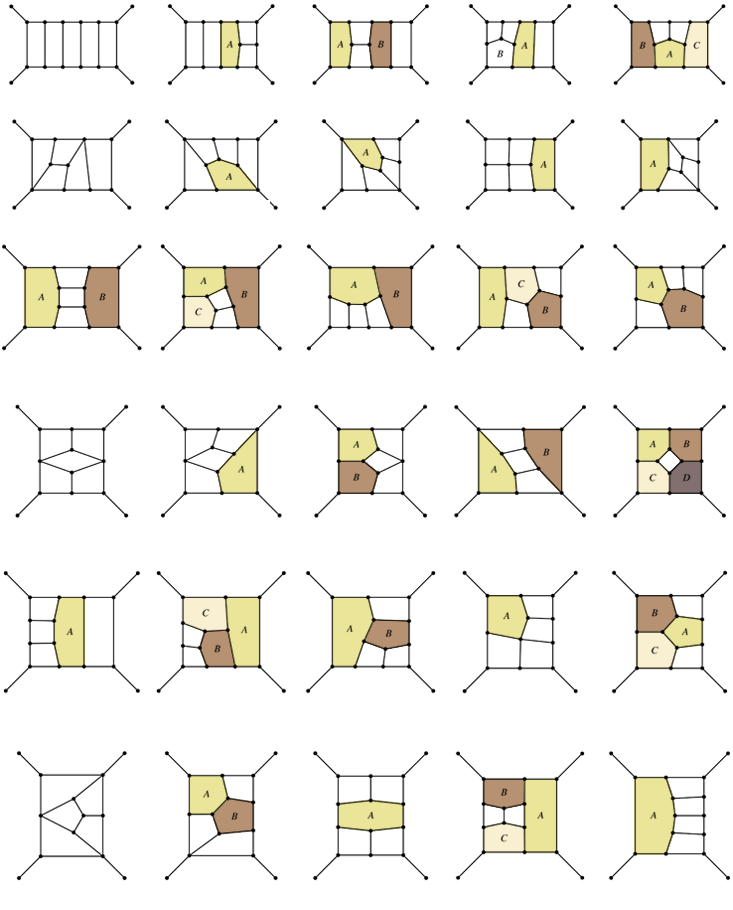
They have found a modest reprieve by invoking yet another symmetry, known as “supersymmetry.” At first blush, supersymmetry sounds outlandish: a doubling of all known types of matter, so that every particle gains a “superpartner” which is almost identical to itself, differing only in the amount of intrinsic angular momentum, or “spin,” that it carries. All those twinned particles lead to exact cancellations among whole classes of Feynman diagrams, greatly reducing the complexity of any given calculation.
Yet even with supersymmetry, any effort to calculate scattering amplitudes involving quarks and gluons has left physicists mired in an ungainly diagrammatic mess. Following Donald Rumsfeld, Feynman diagrams depict at least three types of beasts. There are the known knowns: particles like quarks and gluons that surely exist in our world. Others are the known unknowns: gauge-artifact “ghosts” that exist only in physicists’ imaginations, and are not meant to represent real stuff in the world. And then there are all those superpartners, the unknown unknowns.
Despite decades of concerted searching—even in grand machines like the Large Hadron Collider at CERN—absolutely no empirical evidence has surfaced that superpartner particles exist. But as Rumsfeld famously declared, absence of evidence is not necessarily evidence of absence. Our universe might indeed be governed by supersymmetry, and all those superpartners might one day be discovered. Or they might be nothing more than a convenient mathematical fiction, a souped-up version of ghosts. What seems clear is that supersymmetry remains too convenient to discard: a beloved spherical cow of the microworld.
A New Tool for New Tasks
Nima Arkani-Hamed, a professor at the Institute for Advanced Study in Princeton, is among the most-cited physicists in the history of the universe. Still in his early 40s, he has already accumulated more than twice the number of citations that Richard Feynman collected over a lifetime. Together with his former student and co-author, Jaroslav Trnka, Arkani-Hamed is taking aim at the baroque complexity which physicists have had to face when calculating particle interactions.
On Dec. 6, 2013, Arkani-Hamed and Trnka uploaded a paper describing the amplituhedron onto the preprint server, arXiv.4 Their claim is bold: Here, they write, is a replacement for the venerable Feynman diagram, at least for treating the types of interactions—like the nuclear forces—in which force-carrying particles can scatter directly off each other. When comparing apples to apples (restricting themselves to models that incorporate supersymmetry), their new method can reproduce in just a few lines of algebra the scattering amplitudes that others have painstakingly calculated from hundreds (even thousands) of Feynman diagrams.
To perform their new kind of calculation, Arkani-Hamed and Trnka use their exquisitely simple-looking geometrical constructions, the amplituhedra. Unlike Feynman’s doodles, the new objects are not depicted in space and time; rather, they live in an imaginary, multidimensional mathematical space (see The Amplituhedron) The anchoring points in the new diagrams are coordinates that represent the particles’ momenta, spin, and other variables, rather than locations in space where the particles actually meet.
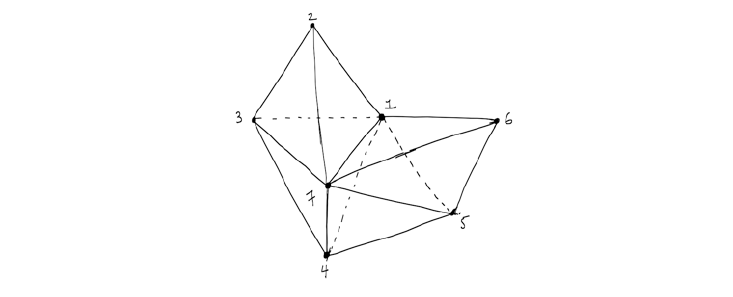
Total momentum and spin must be conserved in any scattering, and hence each amplituhedron is built from closed polygons—essentially, generalizations of a simple triangle. Almost like magic, Arkani-Hamed and Trnka have demonstrated—at least in several tough test cases—that they arrive at the same value for the amplitude of various particle scatterings by calculating the volume of the corresponding amplituhedron, thereby doing an end-run around all those closed-loop, ghost-filled Feynman diagrams.
The result is a breathtaking economy. Physicists like Andrew Hodges at Oxford University and Jacob Bourjaily at Harvard University have marveled at the extraordinary compression and simplification that the amplituhedron approach promises. “The degree of efficiency is mind-boggling,” Bourjaily exclaimed to a journalist recently—an uncanny echo of physicists’ responses to witnessing Richard Feynman first calculate with his diagrams 65 years ago.5
The amplituhedron’s power derives from promoting one kind of symmetry over another. The symmetries that it promotes are those of the amplitudes themselves, governed by very general principles and constraints like conservation of momentum. Swapping an outgoing particle for an incoming one corresponds to rotating the amplituhedron. Some rotations leave the object’s appearance unchanged, just as one can rotate a dodecahedron by certain angles along various directions and not notice any change. To Arkani-Hamed and Trnka, these global symmetries—rotations of the entire amplituhedron that leave its structure unchanged—trump local gauge symmetries.
This means that they discard some types of local symmetries. In fact, they discard—or at least demote—the very idea of “locality” itself. Feynman designed his diagrams assuming that all physical effects arise locally, when one little chunk of matter bumps into another one, at some location x and time t. Feynman didn’t need to know the exact spot where each collision occurred—he integrated over all the possible locations when evaluating his amplitudes—but he nevertheless assumed that each interaction happened at some local position in space and time.
Arkani-Hamed, on the other hand, has a different view of locality. For him, the ultimate prize, the looming mountain in the distance, is a theory of quantum gravity. The amplituhedron is simply a base camp. And because a theory of quantum gravity would presumably explain the emergence of space and time from some deeper substrate or structure, he is eager to sidestep any assumptions about locality—since the notion of locality, after all, presupposes that space and time already exist. While his amplituhedra don’t assume locality, the solutions it produces respect it: Locality is an emergent feature of Arkani-Hamed’s framework, rather than a starting assumption.3
The Future
I can imagine a fractal pattern unfolding. Some time down the road, there could be so many amplituhedra cluttering young physicists’ blackboards (or iPads), that they will feel the need to invent still another device, standing in for hundreds of amplituhedra just as a single amplituhedron stands in for hundreds of Feynman diagrams—and as each Feynman diagram, in turn, represents dozens of lines of algebra. Each new generation tends to reassess the symmetries that had previously been taken for granted. One physicist’s sacred spherical cow becomes another’s inefficient accounting scheme.
For now, though, the amplituhedron and the supersymmetry on which it relies remain unproven ideas. What we do know is that by avoiding local symmetries and enforcing global ones, the amplituhedron allows physicists to calculate complicated interactions with astonishing ease. Even if supersymmetry proves not to be an accurate description of our universe, the success of the amplituhedron suggests that the most basic forces of nature might be governed by a deeper, simpler mathematical structure than what Feynman diagrams have been able to reveal.
On that score, the amplituhedron approach makes the older, Feynman-diagram tools look as helplessly outdated as the room-filling, jerry-built, vacuum-tube computers that, like Feynman’s diagrams themselves, date from the late 1940s. Whether the amplituhedron proves to be exact, or simply a good symmetry-based approximation—the latest spherical cow—will become clear over the coming years, as physicists continue to wrestle with which symmetries should count, and how.
David Kaiser is Germeshausen Professor and Department Head of MIT’s Program in Science, Technology, and Society, and also Senior Lecturer in MIT’s Department of Physics.
Acknowledgements
I am grateful to Michael Segal and Jesse Thaler for helpful comments on an earlier draft.
References
1. Feynman, R.P. Space-time approach to quantum electrodynamics. Physical Review 76, 769-789 (1949).
2. Kaiser, D. Drawing Theories Apart: The Dispersion of Feynman Diagrams in Postwar Physics University of Chicago Press (2005).
3. Bourjaily, J.L., DiRe, A., Shaikh, A., Spradlin, M., & Volovich, A. The soft-collinear bootstrap: N = 4 Yang-Mills amplitudes at six- and seven-loops. preprint arXiv:1112.6432 (2012).
4. Arkani-Hamed, N. & Trnka, J. The amplituhedron. preprint arXiv:1312.2007 (2013).
5. Wolchover, N. A jewel at the heart of quantum physics. Quanta Magazine (2013).






























