Andrew Wiles gave a series of lectures cryptically titled “Modular Forms, Elliptic Curves, and Galois Representations” at a mathematics conference in Cambridge, England, in June 0f 1993. His argument was long and technical. Finally, 20 minutes into the third talk, he came to the end. Then, to punctuate the result, he added:
=> FLT
“Implies Fermat’s Last Theorem.” The most famous unverified conjecture in the history of mathematics. First proposed by the 17th-century French jurist and spare-time mathematician Pierre de Fermat, it had remained unproven for more than 350 years. Wiles, a professor at Princeton University, had worked on the problem, alone and in secret in the attic of his home, for seven years. Now he was unveiling his proof.
His announcement electrified his audience—and the world. The story appeared the next day on the front page of The New York Times. Gap, the clothing retailer, asked him to model a new line of jeans, though he demurred. People Weekly named him one of “The 25 Most Intriguing People of the Year,” along with Princess Diana, Michael Jackson, and Bill Clinton. Barbara Walters’ producers reached out to him for an interview, to which Wiles responded, “Who’s Barbara Walters?”
Out of the ruins of these failures rose deep theories that opened up vast new areas of mathematics.
But the celebration didn’t last. Once a proof is proposed, it must be checked and verified before it is accepted as valid. When Wiles submitted his 200-page proof to the prestigious journal Inventiones Mathematicae, its editor divvied up the manuscript among six reviewers. One of them was Nick Katz, a fellow Princeton mathematician.
For two months, Katz and a French colleague, Luc Illusie, scrutinized every logical step in Katz’s section of the proof. From time to time, they would come across a line of reasoning they couldn’t follow. Katz would email Wiles, who would provide a fix. But in late August, Wiles offered an explanation that didn’t satisfy the two reviewers. And when Wiles took a closer look, he saw that Katz had found a crack in the mathematical scaffolding. At first, a repair seemed straightforward. But as Wiles picked at the crack, pieces of the structure began falling away.
To his mounting horror, Wiles realized that his mistake was more than a minor miscalculation. The oversight wasn’t a crack. At best, it was a gap—left by a faulty anchor point he would have to replace with materials not yet invented. But what if it were a chasm, an irreparable—and humiliating—error that would send the whole thing crashing into the void?
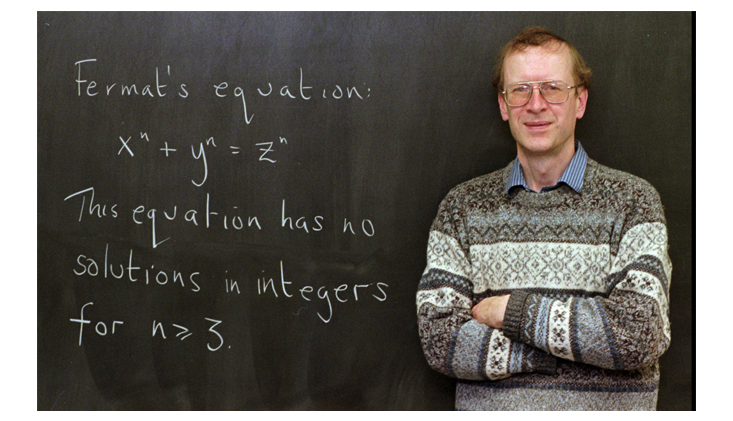
Part of the allure of Fermat’s Last Theorem is its deceptive simplicity. Fermat proposed it in 1637 while studying Arithmetica, a collection of algebraic problems compiled by the Ancient Greek mathematician Diophantus of Alexandria. The book includes a discussion of the Pythagorean Theorem, which describes a relation among the sides of a right triangle. As you may recall, it states that the square of the hypotenuse (the side opposite the right angle) equals the sum of the squares of the other two sides. Or, in mathematical terms, the three sides x, y and z satisfy the equation x2 + y2 = z2.
Diophantus investigated solutions made up only of whole numbers, known as “Pythagorean triples,” of which there are infinitely many. The simplest example is the set 3, 4, and 5. (Hence the familiar “3-4-5” right triangle.) Another is 5, 12, and 13. So is 145, 408, and 433.
Fermat asked a natural next question: Can you find similar triples in higher dimensions? In other words, are there integers that solve the equation a3 + b3 = c3? Or a4 + b4 = c4? Or a10,007+ b10,007 = c10,007?
The answer, Fermat said, is no. There are no sets of whole numbers a, b, c, that satisfy the equation an + bn = cn, where n is a whole number greater than 2. In a margin of Arithmetica, he famously wrote, “I have discovered a truly marvelous demonstration, which this margin is too narrow to contain.”
And, it seemed, he never elaborated elsewhere. After his death, his son Samuel published a new edition of Arithmetica that included all of the notes that Fermat had made in its margins. These observations, typically stated without proof, posed an irresistible challenge. Within a few years, readers had confirmed every one—except the statement about higher-dimension Pythagorean triples. It was the “last” unsubstantiated claim.
For centuries, Fermat’s Last Theorem tantalized professors, amateurs, and cranks alike. (The “prince of mathematicians,” Carl Friedrich Gauss, was among the few early theorists who resisted its charms, dismissing it as “an isolated proposition [that] has very little interest for me.”) The problem was featured in number theory textbooks and popular puzzle books. Science academies offered handsome prizes. And the notoriety of the theorem grew as even the best mathematical minds made limited progress in solving it. Fermat himself had given a proof for n = 4. But although mathematicians later showed that the statement was also true for other n’s, including n’s less than 100 and their multiples, they couldn’t verify that Fermat was right about all n’s. No one could prove he was wrong either.
Wiles had told few people that the proof mathematicians had been awaiting for centuries was now in danger of crumbling at his feet.
Their curiosity, however, brought other rewards. Out of the ruins of these failures rose deep theories that opened up vast new areas of mathematics. In 1847, for instance, the French rivals Augustin Louis Cauchy and Gabriel Lamé, considered two of the greatest mathematicians of their generation, each believed he had proven Fermat’s Last Theorem through complex numbers, an extension of the ordinary, or “real,” number system that includes imaginary numbers. An imaginary number is any number of the form bi, where b is a real number—such as –2 or 5/3—and i = √(-1). A complex number, written in the form a + bi, has a real part (a) and an imaginary part (bi). (Example: –2 + 5i.)
Cauchy and Lamé hung their proofs on the tacit assumption that complex numbers, like real numbers, can be factored into a unique set of primes. The real number 6, for example, always equals 2 x 3. Aside from reordering the factors (3 x 2), no other product will work. But to Cauchy and Lamé’s embarrassment, their German contemporary Ernst Kummer showed that certain complex numbers can be split into prime factors in more than one way. The complex number 6 + 0i, for example, equals 2 x (√2 + i) x (√2 – i) or (1 + √5i) x (1 – √5i).
To restore unique factorization to complex numbers, Kummer invented algebraic objects he called ideals, which proved important in the subsequent development of modern abstract algebra. Writing in the early 1900s, the American algebraist Leonard Eugene Dickson described Kummer’s innovation as “one of the chief scientific triumphs of the last century.”
But the breakthroughs stopped there. After the mid-1800s, most mainstream mathematicians, following Gauss’ lead, gave up on Fermat’s theorem. They had run out of ideas for advancing a solution. And true or false, the problem had no known consequences in other realms of mathematics. Pursuing a proof—or disproof—was a big risk. A promising mathematician could spend a career toiling at a solution and come up dry, with little to show for the effort.

Andrew Wiles first encountered Fermat’s Last Theorem at age 10 and, like many mathematically minded kids, fantasized about solving it. But as a doctoral candidate in mathematics, at Cambridge University, he heeded his advisor’s recommendation to steer clear of that likely dead-end. He chose instead to study elliptic curves, which are useful for cryptography; their graphs look something like the surface of a doughnut.
Then, in 1986, after Wiles had joined the math faculty at Princeton, Ken Ribet, a number theorist at the University of California, Berkeley, laid out an unexpected roadmap for constructing a proof of Fermat’s theorem that would also have far-reaching significance. Three decades earlier, two young researchers at the University of Tokyo, Utaka Taniyama and Goro Shimura, had developed a hypothesis known as the Taniyama-Shimura Conjecture, which compared two seemingly unrelated groups of mathematical objects: modular forms and elliptic curves.
Modular forms are common tools in number theory. They exist in four-dimensional hyperbolic space, a kind of curved space, and are known for their astounding symmetry. Just as a square rotated a quarter turn about its center still looks like the same square, a modular form can be rotated, reflected, or otherwise transformed in many different ways and still end up the same as it started out. Elliptic curves, on the other hand, are algebraic structures. They arise when you graphically plot pairs of complex numbers x and y that satisfy the equation y2 = x3 + Ax + B, where A and B are constants.
“It was so indescribably beautiful; it was so simple and so elegant, and I just stared in disbelief.”
Taniyama and Shimura proposed a bold and radical idea: Modular forms are elliptic curves in disguise. If they were right, then everything mathematicians knew about modular forms could be translated into the language of elliptic curves—and vice versa. Proving the conjecture would be a key step in the grand quest to unify the various disparate branches of mathematics.
It would also prove Fermat’s Last Theorem. In the 1970s, a French doctoral student, Yves Hellegouarch, showed that if Fermat’s theorem were false—that is, if you can find a solution to an + bn = cn—then you should be able to generate an elliptic curve from the equation y2 = x(x – an)(x + bn). A decade later, the German mathematician Gerhard Frey took this logic one step further. Such an elliptic curve could only exist, he conjectured, if the Taniyama-Shimura Conjecture were false. Put another way: If the Taniyama-Shimura Conjecture were true, then Fermat’s Last Theorem was true, too.
Ribet proved that Frey’s guess was correct. Wiles was elated. He could now pursue his childhood ambition of proving Fermat’s theorem without abandoning mainstream mathematics. He retreated to his attic, determined to prove Taniyama and Shimura’s conjecture.
By December 1993, six months after his Cambridge lectures, Wiles had told few people that the proof mathematicians had been awaiting for centuries was now in danger of crumbling at his feet. Only the reviewers of his manuscript and his closest confidents knew about the gap. As rumors circulated that perhaps he hadn’t proven Fermat’s theorem after all, the mathematics community clamored for him to release a draft of his paper. If there was an error, his peers wanted a shot at fixing it.
But Wiles wasn’t willing to share the glory so easily. He kept his secret mostly to himself. Even Ribet, who had been acting as Wiles’ unofficial press liaison, was unable to reach him. “Somehow the expectation was ‘You prove Fermat, and anything less you’re in trouble,’ ” says Peter Sarnak, a Princeton math professor and a friend of Wiles.’
Sarnak urged Wiles to find a collaborator to help repair the gap, if only to “bounce his ideas off somebody who he was comfortable with.” Wiles phoned his former research student Richard Taylor, now a leading number theorist at Cambridge University. At first, they tried what Taylor calls a “localized operation”: They would fix the error by making small corrections to the technique Wiles had used in his incomplete proof.
It didn’t work. So they decided to “cast a wider net and look for other approaches,” Taylor recalls. They worked through the spring and most of the summer, often engaging in long, late-night telephone discussions. “I’d never had such large phone bills,” Taylor says.
But by September 1994, they still hadn’t closed the gap. On the verge of admitting defeat, Wiles took “one last look” at his original approach to try to see precisely where he had gone wrong. In the BBC documentary The Proof, he describes what happened next. “Suddenly, totally unexpectedly, I had this incredible revelation.” There, “out of the ashes” of his failed technique, appeared the very tools he needed to prove another conjecture. He called it “my Iwasawa theory,” an approach he had abandoned three years earlier. Now he could use that theory to prove Fermat’s Last Theorem once and for all. “It was so indescribably beautiful; it was so simple and so elegant, and I just stared in disbelief.”
Armed with Wiles’ new theory, he and Taylor mended the gap within weeks. They published their work, in May 1995, in two papers in the journal Annals of Mathematics. The final proof, and its accompanying discussions, ran 130 pages.
Was this Fermat’s missing proof—the “truly marvelous demonstration” that Arithmetica’s margins were too small to hold? The only sane answer is no. To prove Fermat’s Last Theorem, Wiles employed advanced mathematical instruments and ideas invented long after Fermat’s death. Most mathematicians think Fermat’s theorem was born in error. If he believed he had a proof, he had likely deceived himself.
In the end, though, what mattered was not whether Fermat was right or wrong. The Greeks may have kindled the field of number theory. But Fermat, in a single misguided boast, fanned its dying flames into a major branch of mathematics. His flawed genius bequeathed to us a mathematical heritage that far outweighs the relative triviality of an affirmative answer to his alluring conjecture.
As for Wiles, his error was just an error.
Peter Brown is a freelance science writer and editorial consultant based in New York. Formerly, he was editor-in-chief of The Sciences and Natural History magazines. He holds a bachelor’s degree in mathematics from Princeton University and a doctorate in the philosophy of language from Emory University, in Atlanta.



























