Thank you for your interest in our all-inclusive travel package to the fourth dimension. Here are some of the most frequently asked questions we get from prospective explorers. So far, none of our clients have returned—or even sent a text—so we can only share what our scientific consultants say will likely occur.
How do I get there?
You will stand at the center of a large sphere. As you might expect coming from our current three-dimensional reality, you will be able to move left or right, forward or back, and up or down. However, we ask that you keep as still as possible while our patented 4-D BOOST® technology propels you away from all points on the surface of the sphere at once, lifting you into the fourth dimension.
Huh? The tech-support guy at my office said the trip would involve cubes.
Cubes are just useful tools for understanding four-dimensional space. For example, let’s start with a (1-D) line segment. By adding a parallel segment and connecting it with two perpendicular segments, all equally sized, we can make a (2-D) square. With us so far? Similarly, if we take two parallel squares and connect them with more perpendicular segments, we get a (3-D) cube. Now here’s where things get tricky. In the next iteration, two parallel cubes plus perpendicular connectors creates a (4-D) hypercube, or tesseract.1
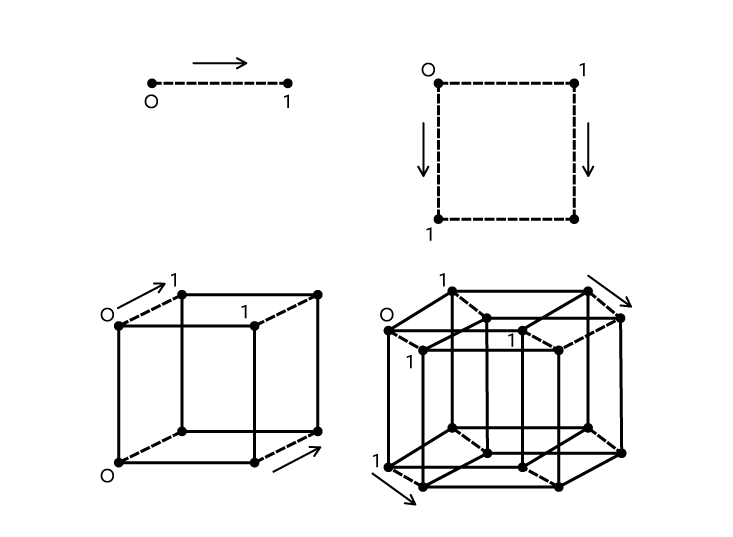
Of course, being 3-D creatures, we can’t fully wrap our minds around this 4-D construction. The late mathematician William Thurston believed this was because our brains evolved to process linear, analytic information in one area and geometric shapes in another. So while we can easily solve equations with four or more variables, allowing us to dream up and manipulate objects in higher and higher dimensions, we struggle to perceive them. “The fourth dimension is kind of conceivable as right angles to the three dimensions we have,” Australian mathematician (and stand-up comedian) Matt Parker tells us in his book Things to Make and Do in the Fourth Dimension. “But we cannot imagine what the fourth dimension is.”2
So you’re saying I can’t see any photos of my hotel before I get there?
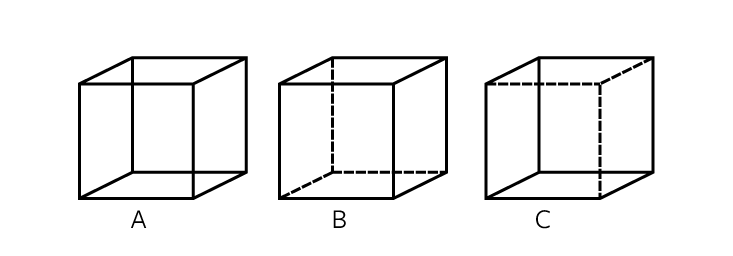
Unfortunately, no. You can, however, get a glimpse of the fourth dimension through an optical illusion called the Necker cube (labeled A in the figure below). There are two ways to interpret this shape: as a box oriented slightly left and down (B), or as its mirror image (C). If you stare at the Necker cube long enough, it appears to flip back and forth in what mathematician Rudy Rucker calls a “twinkling rearrangement.” Eventually, the twinkling may appear as one continuous motion. But, as Rucker points out in his book Geometry, Relativity and the Fourth Dimension, “this motion can only be continuous if it is a rotation in 4-D space.” That’s because a rotation in three dimensions can’t produce a mirror image. “So perhaps we can actually produce a 4-D phenomenon in our minds!”3
Hmm…maybe this isn’t for me.
Don’t get too hung up on the mechanics. Remember, you don’t have to know how roller coasters work to enjoy the ride.
OK, so what should I pack?
We will supply you with everything we expect you will need, including:
A heat shield. The extra dimension disrupts the delicate balance between gravity and centrifugal force that keeps Earth revolving in a stable orbit. According to the late physicist Richard Morris, once you arrive in 4-D space, the planet will begin spiraling toward the sun.4
Polarized lenses. Because light propagates in a direction perpendicular to its electric and magnetic fields, it’s hard to predict how it will behave when you add another set of perpendicular coordinates. So sunglasses can’t hurt. A retina shaped like a sphere rather than a disc, i.e., a “third eye,” would also be useful, according to Rucker. Due to pending litigation, however, we no longer offer that surgery.
Earplugs. Because sound waves in even dimensions double back on themselves, like ripples in a pond, everything will sound echo-y and drawn out, and you may be constantly bombarded with noise. For example, the start of Beethoven’s Fifth Symphony (dum dum dum DAH) would get “mushed out,” sounding more like ladidadiladidadidadidididi, says Clifford Pickover, author of Surfing Through Hyperspace. Don’t be alarmed if you can’t understand your fellow travelers when they speak to you.
Velcro shoes. Just as a looped piece of string lying on a plane will straighten out when you lift one end into the third dimension, a 3-D knot will easily untie in 4-D space. We don’t want you to trip on your laces (in several directions at once) when you get there.
A closed loop of string, two wooden rings, and a seashell. As the German astrophysicist Johann Zöllner advised in 1878, you will use these items to confirm that you have in fact reached the fourth dimension. You should be able to tie a knot in the string without cutting the loop, link and unlink the rings, and flip the orientation of the spiral on the seashell.
Will I be attacked/mugged/hit on by a 4-D creature?
We cannot rule out this possibility (see waiver). Having far more neural connections in their brains, 4-D beings will be super smart. And as Parker informs us, they “would have the ultimate tactical advantage.” By way of analogy, let’s say that you, a 3-D creature, wanted to torment a 2-D creature. Your victim would be constrained to a flat surface while you could hover above it, out of sight. You could see and access all of its insides. If you reached a hand into its world to grab it, your fingers would appear suddenly as floating, disjointed circles. Similarly, a 4-D attacker could materialize in your 3-D view out of the blue and pluck the money right out of your wallet, or harvest your organs, without laying a finger on your clothes or skin.

Will 4-D creatures speak English?
That’s hard to say. Following Pickover’s advice, we recommend that you instead communicate in binary code. (The rules of math apply to all dimensions, no matter which one you live in.) For example, you might try blinking, or raising your arms up and down, and hope someone notices. A 4-D creature could likewise send you a message by inserting and removing a 4-D object from your 3-D view, just as you might insert and remove a 3-D object from a flat plane to communicate with a 2-D being.5
Is the water safe to drink?
It should be okay—if water exists at all. There is some uncertainty about this. Some physicists have argued that hydrogen atoms (the H’s in H2O) won’t be stable in four dimensions because the extra dimension screws with quantum forces, in much the same way it messes with gravity. But a team of mathematicians found that, if you assume higher dimensions don’t follow the usual laws of electromagnetism, you can have stable hydrogen atoms after all.6 To play it safe, we suggest you drink plenty of liquids before your departure.
What souvenirs should I buy?
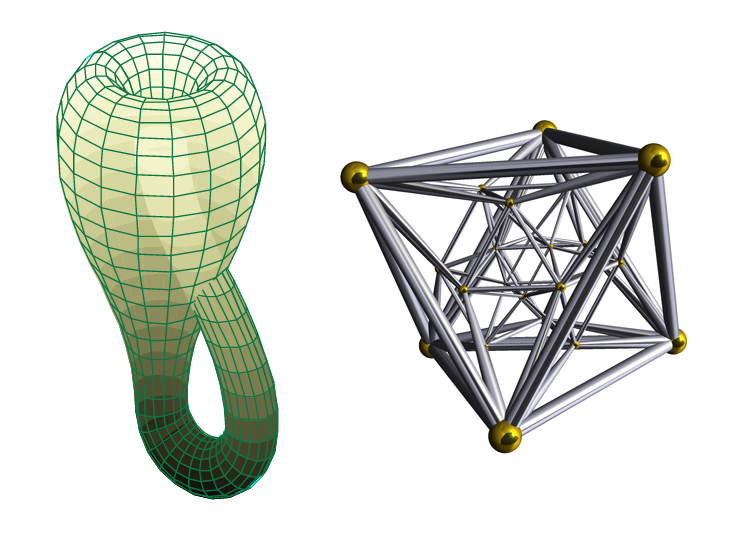
See if the gift shop has any Rubik’s Hypercubes.™ You might have already tried an online version of this puzzle, built by some clever software engineers in California, but remember, this is just a 2-D projection of a 3-D projection of the 4-D cube. The real thing will be way more awesome. Parker also recommends key chains with his favorite 4-D shape: a hypercube turned inside out, known as a hyperdiamond (or octacube). It’s the only one of six 4-D analogs of the Platonic solids—regular, convex polyhedra with equivalent faces, such as a cube or a tetrahedron—that has no equivalent in 3-D. Another fun memento is a Klein bottle, which has only one side (no “inside” and “outside”) and no boundary, meaning it contains itself. It can only exist in four dimensions because it must pass through itself without making a hole.
However, you may want to save your money. We’re sure 4-D vendors gouge 3-D tourists. Besides, the items you bring home won’t be nearly as impressive back in 3-D space.
What if I’m not satisfied?
Please understand that we cannot foresee every possible outcome, and so cannot offer refunds. However, if your body is rotated into its mirror image, or pulled apart in eight directions—and there is evidence that this occurred, such as a DNA-certified organ that comes flying back into 3-D space—we will issue your survivors a $50 voucher for our gift shop.
Chip Rowe is a writer based in New York.
References
1. Gardner, M. The Colossal Book of Mathematics W.W. Norton & Co., New York, NY (2001).
2. Parker, M. Things to Make and Do in the Fourth Dimension: A Mathematician’s Journey Through Narcissistic Numbers, Optimal Dating Algorithms, at Least Two Kinds of Infinity and More Farrar, Straus and Giroux, New York, NY (2014).
3. Rucker, R. The Fourth Dimension: Toward a Geometry of Higher Reality Houghton Mifflin Co., Boston, MA (1984).
4. Morris, R. Cosmic Questions: Galactic Halos, Cold Dark Matter and the End of Time Wiley, New York, NY (1993).
5. Pickover, C. Surfing Through Hyperspace: Understanding Higher Universes in Six Easy Lessons Oxford University Press, New York, NY (1999).
6. Burgbacher, F., Lammersahl, C., & Macias, A. Is there a stable hydrogen atom in higher dimensions? Journal of Mathematical Physics 40, 625-634 (1999).































