You’re thinking about time all wrong, according to our best physical theories. In Einstein’s general theory of relativity, there’s no conceptual distinction between the past and the future, let alone an objective line of “now.” There’s also no sense in which time “flows”; instead, all of space and time is just there in some four-dimensional structure. What’s more, all the fundamental laws of physics work essentially the same both forward and backward.
None of these facts are easy to accept, because they’re in direct conflict with our subjective experience of time. But don’t feel too bad: They’re hard even for physicists to accept, an ongoing tension that places physics in conflict not just with common sense but also with itself. As much as physicists talk about time symmetry, they do not allow themselves to invoke the future, only the past, when seeking to explain occurrences in the world.

When formulating explanations, most of us tend to think in terms laid down by Isaac Newton over 300 years ago. This “Newtonian Schema” takes the past as primary and uses it to solve for the future, explaining our universe one time-step at a time. Some researchers even go so far as to think of the universe as the output of a forward-running computer program, a picture that is a natural extension of this schema. Even though our view of time has changed dramatically in the last century, the Newtonian Schema has somehow endured as our most popular physics framework.
But imposing old Newtonian Schema thinking on new quantum-scale phenomena has landed us in situations with no good explanations whatsoever. If these phenomena seem inexplicable, we may just be thinking about them in the wrong way. Much better explanations become available if we are willing to take the future into account as well as the past. But Newtonian-style thinking is inherently incapable of such time-neutral explanations. Computer programs run in only one direction, and trying to combine two programs running in opposite directions leads to the paradoxical morass of poorly plotted time-travel movies. In order to treat the future as seriously as we treat the past, we clearly need an alternative to the Newtonian Schema.
And we have one. Most physicists are well aware of a different framework, an alternative where space and time are analyzed in an even-handed manner. This so-called Lagrangian Schema also has old roots and has become an essential tool in every field of fundamental physics. But even physicists who regularly use this approach have resisted the last obvious step: thinking of the Lagrangian Schema not just as a mathematical trick, but as a way to explain the world. Perhaps we haven’t been taking our own theories seriously enough.
The Lagrangian Schema doesn’t just allow future-based explanations. It demands them. By treating the future and the past on the same footing, this framework avoids paradoxes and makes new explanatory opportunities available. And it just might be the viewpoint that physics needs for the next major breakthrough.
The first step toward understanding the Lagrangian Schema is to fully set aside the temporal “flow” of Newtonian thinking. This can best be done by treating spacetime regions holistically: considering the full duration all at once, rather than as sequential frames of a movie. We can picture regions of spacetime as bounded four-dimensional structures, with not just spatial boundaries, but also temporal boundaries—the initial and final bookends of the region.
All of classical physics, from electricity to black holes, can be expressed via the simple Lagrangian-based principle of “least-action.” To use it on a spacetime region, you first describe how physical parameters are constrained over the entire boundary. Then, for each set of possible events inside that boundary, you calculate a quantity called the “action.” The set of events with the lowest value of the action is the one that will actually occur, given the original boundary constraints and a few other technical caveats.
It is hard to accept that events might be explained by what goes on in the future.
For instance, when a ray of light travels from point A to point B, the action corresponds to the amount of travel time. The actual path is the fastest route, given the intermediate obstacles. By this way of thinking, a light ray bends at a glass interface simply because it minimizes the overall travel time. The Lagrangian Schema works a bit differently in quantum physics and yields probabilities rather than decisive predictions, but the basics are the same: Spacetime boundary constraints are still imposed all at once.
By Newtonian logic, this sounds quite strange. The light ray at A seems to possess foreknowledge (about point B and future obstacles), vast computational ability (to survey the different paths), and agency (to choose the fastest one). But this strangeness is merely evidence that Newtonian and Lagrangian thinking don’t mesh—and that we probably shouldn’t anthropomorphize light rays.
Instead of explaining events via only the past, the Lagrangian Schema starts with the entire boundary constraint—including, crucially, the final boundary. If you don’t impose a final constraint—for light rays, the location of point B—this approach fails to give the proper answer. But if used properly, the success of the mathematics indicates a clear logical priority of the boundary constraint: The boundary of any spacetime region explains the interior.
The Lagrangian approach provides the most elegant and flexible account of known physics, and physicists often prefer it. Still, despite the wide applicability of Lagrangian-based principles, even the physicists who use them don’t take them literally. It is hard to accept that events might be explained by what goes on in the future. After all, there are obvious distinctions between past and future. Given that we see such an evident arrow of time, how could future boundaries possibly matter just as much as past ones?
But there’s a way to reconcile the Lagrangian Schema with our causal experience. We just have to think sufficiently big, without losing sight of the details.

Suppose you take a flash photograph of a statue. Each ray of light obeys the least-action principle, giving a perfectly time-symmetric account of its path. But taken together, there’s an obvious asymmetry: The initial boundaries A are all clustered together at the flash, while the final boundaries B are spread out over the statue. Furthermore, it’s perfectly clear that the spreading of light from A is a much better explanation of the illumination at B than vice-versa. Even if the ray paths were viewed in reverse, no one would plausibly claim that the light was concentrated at the flashbulb because of complex patterns of light on the statue.
One lesson here is that satisfying explanations account for complicated events in terms of simple givens. They take a single fact, with just a few relevant parameters, to explain a plurality of events. This should be evident no matter which schema one is using.
But this asymmetry of A and B is not a rebuttal to the Lagrangian perspective, which merely says that A and B together can best explain the details of what happens in between. Even in the Lagrangian Schema, A and B are not independent of each other. To see how they’re related, we need to think bigger. According to the boundary framework of the Lagrangian Schema, explanations don’t chain. They nest. In other words, we don’t picture event A leading to event B leading to event C. Instead, we treat a small spacetime region in its entirety; then we treat this region as part of a larger region (in both space and time). Applying the same Lagrangian logic, the larger boundaries should now explain everything in their interior, including the original boundaries.
If the future can constrain the past, why are the consequences confined to the quantum level?
Running this procedure for the statue example, we find the same asymmetry of bulb and illumination writ larger. That is, we find a satisfying explanation for the camera flash in its past, but we don’t explain the illumination of the statue by looking to its future. Then we can enclose that larger system in an even bigger one, and so on, until we have gone all the way out to the cosmological boundary—the external constraints on our entire universe. To the best of our knowledge, we see the same asymmetry at that scale: an unusual, smooth distribution of matter near the big bang, and greater disorder in the future.
Looking at ordinary spacetime regions from a Lagrangian perspective, the fact that initial boundaries (light rays diverging from flashbulbs) are simpler than final boundaries (lit statues) is strong evidence that our closest cosmological boundary lies to our past. The consistency of this ordering implies there is no corresponding cosmological boundary in the comparable future. So given the big bang as our best explanation of the obvious features of our universe, the evident direction of time is essentially no different from the spatial temperature gradient you feel when standing next to a cold window. In neither case is space or time asymmetric; it’s just a matter of where you are located relative to the nearest boundary constraint.
On the classical scales that we typically observe, we don’t get any new information from the future boundary that we didn’t already have in the past. If this held true at all scales, the Lagrangian Schema would be in trouble, because the future boundary wouldn’t really matter at all. But in fact it isn’t true when we get down to the level of quantum uncertainty: Microscopic future details cannot be deduced from only the past. And the quantum scale is where the real power of the Lagrangian Schema becomes evident.
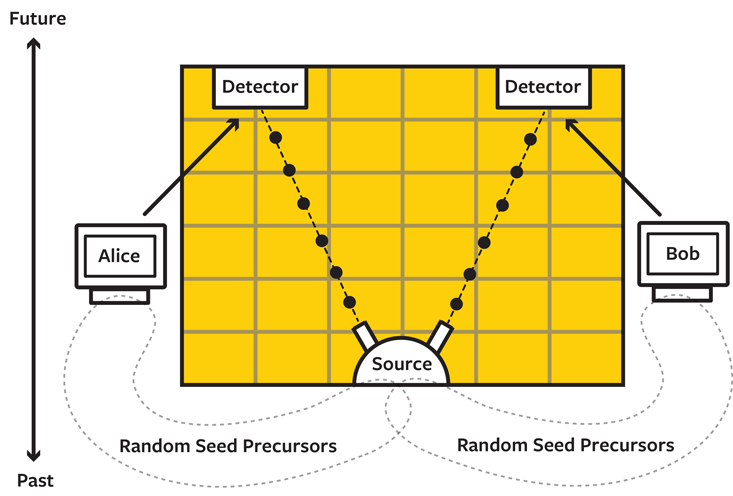
Quantum entanglement is a concept that defies Newtonian Schema explanations. The details don’t matter for our purposes, so let’s consider the skeletal outline of a typical entanglement experiment (see A Tangled Tale). The apparatus in the center creates two particles. The left particle is sent to a detector controlled by one computer (“Alice”), and the right particle is sent to a distant detector controlled by another computer (“Bob”). The detectors measure their respective particles in one of several different ways, decided by independent random numbers. As the Irish physicist John Bell famously demonstrated in the ’60s, the measurement results of these experiments are correlated in ways that firmly resist our usual attempts at explanation.
In particular, the particles’ shared past isn’t sufficient to explain the measured correlations, at least not over the full range of measurement settings that Alice and Bob could randomly choose. Of course, many scientists want to explain these results physically and aren’t particularly happy with merely describing the correlations via bare mathematics. Left at a loss, they find themselves invoking mysterious entities not properly existing anywhere in space or time (begging for an explanation in their own right) or perhaps even traveling faster than light (in blatant violation of everything we know about Einstein’s theory of relativity).
Why can’t we use quantum phenomena to send messages into the past?
Leaving these desperate options aside, everyone agrees that if only the particles could anticipate Alice’s and Bob’s random settings in advance, a natural explanation could still be found. But most proposals to give the particles this information sound even more desperate, requiring what amounts to a form of cheating: The particles would somehow sniff out all the inputs to Alice’s and Bob’s random number generators and use that information to predict the future detector settings.
Almost no one buys this as a worthwhile explanation of the entanglement experiments, just as you wouldn’t accept an “explanation” of a localized camera flash as being due to the complicated details of a lit statue. Such conspiratorial accounts violate our reasonable standards of explanation: The putative mechanism is vastly more complicated than the simple outcomes it is trying to explain.
In the statue example, the obvious solution is to look to the simpler boundary—the flash—for the best explanation. For quantum entanglement, when using the Lagrangian viewpoint, a reasonable explanation is nearly as obvious. The explanation is not in the complex precursors to the detector settings, it’s in the simple future detector settings themselves.
The mysterious entangled particles exist in the shaded spacetime region in the figure, and the boundary of this region includes both their preparation and their eventual detection. The settings chosen by Alice and Bob are physically expressed by the actual detectors, on the final boundary—exactly where the Lagrangian Schema tells us to look for explanations. All we need to do is allow the particles to be directly constrained by that future boundary and a simple explanation of entanglement experiments becomes available. In this case, it’s the future and the past together that can best explain the observations.
Quantum entanglement may not be the only mystery that we can dissolve by taking the future seriously as an explanation. Other quantum phenomena may also turn out to have an underlying simpler account, an explanation that could reside in ordinary space and time without any action at a distance. Maybe the probabilities in quantum theory will turn out to be like probabilities in every other scientific discipline: simply due to parameters that we don’t know (because some of them lie in the future).
Any such line of research will certainly raise significant questions. If the future can constrain the past, why are the consequences confined to the quantum level? Why can’t we use quantum phenomena to send messages into the past? At what scales does the cosmological boundary dominate, and how exactly should we generalize Lagrangian-based approaches to make this all work?
Addressing such questions might not just help physics; it might also inform how we see ourselves as part of our four-dimensional universe. For example, according to the Lagrangian Schema, microscopic details in any region are not entirely constrained by the past boundary. On the level of the atoms in your brain, there are relevant but unknown constraints in the future. Perhaps this line of thinking could even help to explain our sense of free will, by providing a new sense in which the future is not purely determined by what has come before. Certainly it would require us to rethink the idea that there is a neat and objective difference between a fixed past and an open future.
Almost every time science has found a deeper, simpler, more satisfying explanation, it has led to a cascade of further scientific advances. So if there is a deeper account of quantum phenomena that we haven’t yet grasped, mastering that deeper level could lead to crucial advances in the vast array of technologies that utilize quantum effects. Mistaken instincts have certainly slowed past physics advances, and our instincts about time are as strong as they come. But there is a clear path forward to explaining some of nature’s deepest mysteries, if we can simply make ourselves look to the future.
Ken Wharton is a physics professor at San Jose State University, formerly an experimentalist working on high-intensity lasers, now a theorist working to unify physics by rethinking our conventional notions of time.
Huw Price is a philosopher professor at the University of Cambridge who is best known for exploring the time symmetry of physics. Beginning this fall, he will be director of the Leverhulme Centre for the Future of Intelligence to study the ramifications of artificial intelligence.
The lead art was created using an image from Christian Mueller / Shutterstock






























