As conscious beings, we are constantly aware of the relentless march of time. You can make an egg into an omelet, but you can’t turn an omelet back into an egg. Dropped glasses shatter and do not reassemble themselves. Above all, we age and become decrepit; there is no return to youth.
But this is a great scientific mystery. There is nothing in the form of the laws of nature at the fundamental microscopic level that distinguishes a direction of time. They are time-symmetric. But the behavior of macroscopic objects around us is subject to the famous second law of thermodynamics, according to which disorder (as measured by entropy) always increases with time. This puts a direction, or arrow, of time into phenomena. The classical studies by Maxwell and Boltzmann in the second half of the 19th century assumed the existence of atoms and showed, on the basis of reasonable laws, that non-uniform distributions of atoms would always have a tendency to be washed out into a state with a uniform temperature distribution.
This initial work took no account of gravity. Gravity presents many puzzles because it gives rise to “anti-thermodynamic” behavior: Under its influence, uniformly distributed matter tends to break up into clusters. As of now, no one knows how to describe this behavior using an entropy-type concept. This is all the more puzzling because Einstein’s wonderful theory of gravity—his general theory of relativity—does show that when black holes form they do have thermodynamic properties and possess a colossal entropy. What no one has been able to do is define gravitational entropy for the rest of the universe.
The most popular ideas, initiated by the great gravitational theorist Roger Penrose, attempt to define this gravitational entropy for the rest of the universe in terms of the degree of non-uniformity of the gravitational field. Cosmological observations indicate that the early universe began in an exceptionally uniform state, which, if Penrose is right, corresponds to a very low entropy. Since then entropy has greatly increased, above all through the formation of black holes. But this in turn raises a question: Given time-symmetric laws and the fact that high-entropy states are vastly more probable than low-entropy states, what explains the exceptionally low entropy of the universe’s initial state?
Gravity presents many puzzles because it gives rise to “anti-thermodynamic” behavior.
A common assumption among scientists today is simply that, for some as yet unknown, possibly quantum-mechanical reason, the universe just did begin in such a state. This is the “past hypothesis.” It invokes the fact that all standard explanations in physics involve both laws and initial conditions: The outcome of any laboratory experiment is determined both by laws and by the conditions under which it is started. The past hypothesis extends this traditional way of thinking to the whole universe. It relies on law and on an initial condition.
But the reliance on an unexplained initial condition to explain two of the most striking features of the universe—the growth of entropy around us alongside the steady growth of structure in the universe at large—leaves Penrose and others like myself dissatisfied. What drives scientists is the desire to explain and understand phenomena. We all want to emulate the way Charles Darwin explained so much with just four words: evolution by natural selection. In the case of time’s arrow, it is literally a matter of life and death, for we all march together in the same direction from birth to the grave. What is it that puts such striking order into the world?
My collaborators and I have hit upon a potential explanation that relies on law alone.1 We came to it by chance, and it may or may not be correct. However, it has the merit of showing how at least one time-symmetric law (gravity) always leads to an observed unidirectional growth of structure.
The basis of our explanation lies in the simplest “toy” model one can make of the universe: three equal-mass particles that interact in accordance with Newton’s law of universal gravitation. The three particles move relative to each other, tracing out paths in infinite space rather like three endless strands of spaghetti held in fixed mutual positions. Each triplet of curves will have a different shape from any other. Under restrictions that are reasonable if we are aiming to model the whole universe,1 virtually all path triplets described by the particles will be of the kind shown in the Figure, “A toy model of the universe.”
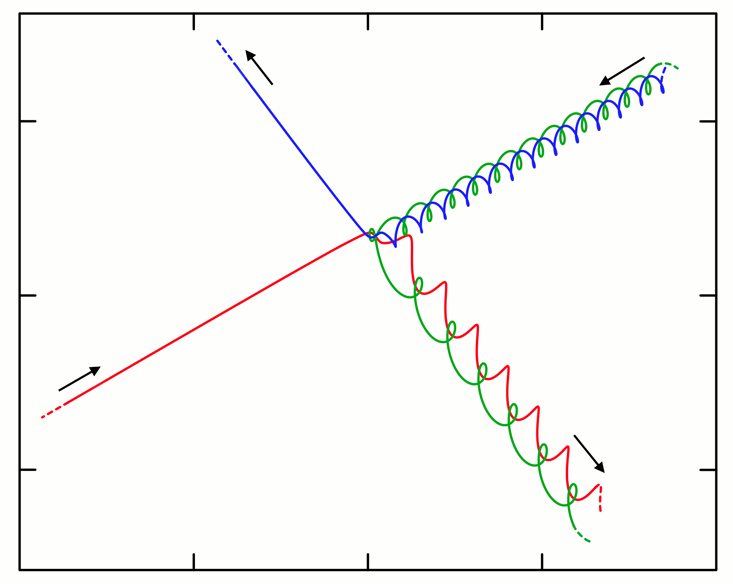
As indicated by the arrows in the Figure, we see one particle coming from the bottom left while the other two particles are orbiting each other and coming from the top right. There is a complicated interaction when they meet, as a result of which there may, as shown, be a swapping of partners. Then the single particle flies off to the top left, while the new pair goes to the bottom right. It may also happen that there is no swapping of partners.
In either case, the key point is that, because the underlying law does not distinguish a direction of time, the arrows can be reversed and the story reads equally well in the opposite direction. If one considers the complete solution,2 there is no way in which the law that governs the process enables one to identify a beginning or end of the story. It is quite impossible to say that time flows in one direction rather than the opposite.
However, there is an intriguing alternative to considering the complete solution in the figure. Let’s start with what seems real. In any instant, three particles form a triangle. To say it has a size, we would need a ruler. But that would be something extra, and we want to model the universe by the three particles and nothing else. That just leaves us with the shape of the triangle, which is determined by two angles. Since the shape changes continuously and can be assumed never to repeat exactly, then if we were given all the triangles we could lay them out unambiguously in one of two definite orders, each the opposite of the other.
What now are instants of time? There is no clock in our model to tell them. All we have is shapes. Since they are all different and can be arranged in a line, let’s call them the instants. Since remote antiquity the changing shape of the moon has been used for dating purposes. It still controls the Islamic calendar and the Christian and Jewish feast days. Taking the shapes of the universe as instants makes it into the ultimate moon.
It is literally a matter of life and death, for we all march together in the same direction from birth to the grave.
Having established the importance of shape, let us interpret the Figure in terms of how the shape changes, starting with the central region where all three particles interact strongly. Typically, this is a very irregular region, and the shapes change accordingly. It may be likened to “primordial chaos.” Let’s arbitrarily call this central region the “beginning” of time.
Now consider the diagonal of the Figure in which the arrows are shown pointing away from the “primordial chaos.” The line going up to the left represents a single particle, the twisted “spaghetti” strands going down to the right represent a pair that settles ever more stably into an orbiting pair. This pair serves as a periodic process that defines a clock. Each successive “tick” occurs when one particle of the pair crosses the line joining the center of mass of the particle to the third particle. That is when the universe is in the special shape of three particles on a line. So our toy universe really is like the moon.
But now let’s think if there is any sense in which a direction, or orientation, of time can be identified in the Figure. I pointed out that in our universe two opposite effects define the same direction of time. The growth of disorder (entropy) in restricted regions, while simultaneously the universe on the large scale is getting ever more richly structured as galaxies, stars, and planetary systems form. Our model is far too simple to model the growth of entropy, but it does model the growth of structure.
Indeed, one can regard the orbiting pair as a “galaxy,” the formation of which as it emerges from the “primordial chaos” can be followed step by step in the Figure. Thus, if we restrict attention to the considered diagonal and define the direction of time by the growth of structure out of chaos, we obtain a story that, in its most basic features, models rather well what cosmologists observe in the universe. It’s the story of a universe whose overall shape changes in a unidirectional manner.

But there is of course the other diagonal, the one running from bottom left to top right. If we reverse the arrows on it and again take the “primordial chaos” as the birth of time, we get another “history of the universe,” different from the first but qualitatively of the same kind. We have two quite different histories within one solution! This is all done with just three particles. For reasons given in our paper, the same kind of thing happens if the number of particles is increased arbitrarily. Remarkably, there is always a region of irregular chaotic motion—a “primordial chaos”—from which two and only two effectively independent paths emerge. Note that the simplest version of this model has three particles, since a clock could not be defined with only two.
As god-like theoreticians, we can look at the Figure in its entirety and see that it defines no overall direction of time. But any observer within the Figure’s universe will necessarily be in one of the two parts I have called histories (one of the two diagonals). Restricted to it, they would observe the key attributes that we associate with time: a division into past, present, and future; clocks that measure time; and progressive growth of structure that defines an arrow of time. They would therefore take the “primordial chaos” at the Figure’s center to be a past that caused the ordered present.
It should be said that it is the nature of each history rather than the duplication of histories that is important. Although the basic kind of behavior is not changed by adding particles, we cannot expect Newton’s theory to model Einstein’s general relativity. However, it is interesting that there are some very special solutions of the Newtonian theory that are relatively good models for Einstein’s.
In these, the “primordial chaos” is not an irregular region but one in which all the particles are at exactly the same point, from which they initially emerge in a rather uniform distribution, which then becomes irregular before stable structures form. In this case, there is just one diagonal, at the middle of which all the particles are at one point. This is a promising model of the Big Bang of modern cosmology.

The point I want to make is this: All solutions of the model exhibit unidirectional growth of structure out of “chaos.” Very basic elements of the law mean that the growth cannot reverse. The underlying reasons are given in the paper by my collaborators and myself. Moreover, if, as in cosmology, we define the direction of time by the growth of structure, all solutions supply a direction of time even though they are generated by a law that, in itself, does not distinguish a direction of time.
 The three-particle toy model questions our instinctive notion of causality, according to which something in the past causes what happens now. In the Figure, there is no past that causes and explains any present. Causality does not work that way. Law is the only cause, including the case of the special solutions with only one history. All solutions that obey the law exist in a timeless eternity like paths in a landscape or valleys in a mountain range. It’s wrong to read causality through time into the solutions. Paths simply are. However, they can lead from less to more structured regions. The model proves that law alone, without any special initial condition, may be sufficient to explain time’s arrow.
The three-particle toy model questions our instinctive notion of causality, according to which something in the past causes what happens now. In the Figure, there is no past that causes and explains any present. Causality does not work that way. Law is the only cause, including the case of the special solutions with only one history. All solutions that obey the law exist in a timeless eternity like paths in a landscape or valleys in a mountain range. It’s wrong to read causality through time into the solutions. Paths simply are. However, they can lead from less to more structured regions. The model proves that law alone, without any special initial condition, may be sufficient to explain time’s arrow.
Now let’s return to our own universe, which exhibits unidirectional change. In the traditional chronology, the early universe was vastly more uniform than today’s. Observations of the microwave radiation that bathes the universe reveal random fluctuations in temperature and mass density of only about one part in 10,000.
Taking this state as an initial condition, cosmologists can explain remarkably well how the present universe with its incredibly rich structure and huge density contrasts came into being. It is therefore very natural to say the microwave background existed before our present universe and through a causal mechanism gave rise to it. It seems utterly bizarre to say the present universe caused the microwave background. But, in the final analysis, this is a conclusion based on instinct, not hard fact—and instinct has often hindered progress in science.
This work is just a start. The fact that all this emerges already from the interaction of just three particles is due to the beautiful simplicity of Newton’s law of gravity and certain architectonic structures it possesses. Einstein’s general relativity has them too but is a much richer theory, so we cannot say yet whether in that case law alone will suffice to create an arrow of time without the crutch of a special initial condition. If it does, though, one of the intuitions that most people, including many scientists, find very hard to shed—that time is real and does flow—may well be an illusion.
Julian Barbour is an independent theoretical physicist who has devoted much research into the nature of time. Since 2008, he has been a visiting professor in physics at the University of Oxford.
Lead image (and detail): Birth of the Universe by Antoine Pevsner, 1933. © CNAC/MNAM/Dist. RMN-Grand Palais / Art Resource, NY
Reproduction, including downloading of Antoine Pevsner works is prohibited by copyright laws and international conventions without the express written permission of Artists Rights Society (ARS), New York.
Footnote
1. This article is based on a paper by Tim Koslowski, Flavio Mercati, and myself. Readers can also view a talk by me, here. My thanks to Flavio for the use of his figure.



























