Reprinted with permission from Quanta Abstractions
A recent advance in geometry makes heavy use of Ramsey’s theorem, an important idea in another field—graph theory. Ramsey’s theorem states that in any graph where all points are connected by either red lines or blue lines, you’re guaranteed to have a large subset of the graph that is completely uniform—that is, either all red or all blue.
Equivalently, you can go the other way: Pick how big you want your uniform subset to be. Ramsey’s theorem states that somewhere out there there’s a graph in which a subset of that size must arise.
It’s not obvious why this is true. Why can’t there be a graph where lines of different colors remain completely jumbled together?
I put this question to Jonathan Jedwab, a mathematician at Simon Fraser University in British Columbia. He responded with this example, which provides a graphical intuition for why the theorem is true.
Let’s take a simple case where you’re looking for a subset of at least three lines that are completely uniform. A hexagonal graph is guaranteed to give you that subset. How?
Start with six points representing six people at a party. Any two people at the party will either know each other ahead of time or not know each other. If they know each other, color the line between them red. If they don’t know each other, color the line between them blue. Every point will then have five lines coming out of it; at least three of those five lines must be either red or blue.
A proof of Ramsey’s theorem would mean showing that no matter how you connect the people, you’re guaranteed to end up with a triangle (a uniform subset with three lines) that is either all blue or all red.
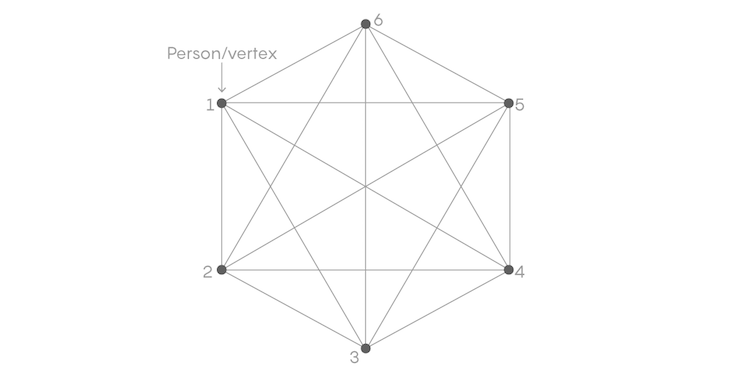
Let’s think about Person 1. At least three of her five lines are going to be red or blue. Given that, imagine she knows the people in positions 2, 4, and 5, and color those lines red.
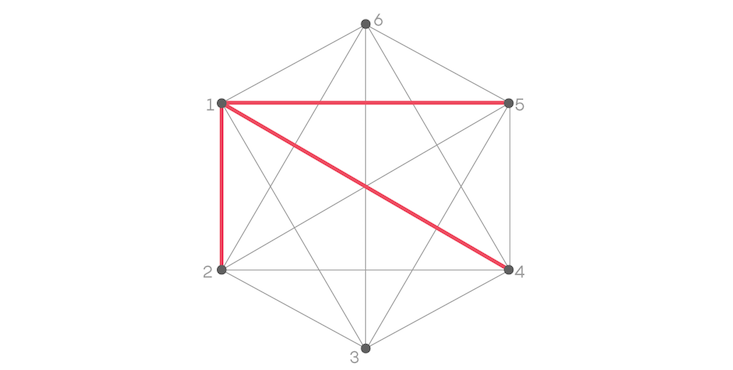
Now, think about Person 2 and Person 5. If they know each other we’d color the edge red and have a triangle of all one color, which we’re trying to avoid. So color that edge blue.
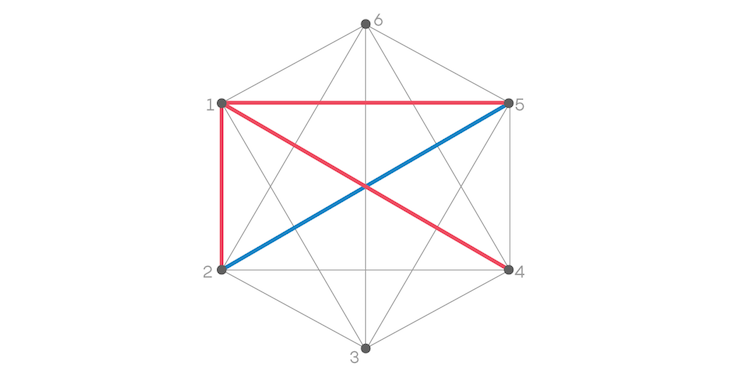
Then think about the relationship between Person 4 and Person 5. Again, to avoid a red triangle, we have to color that edge blue.
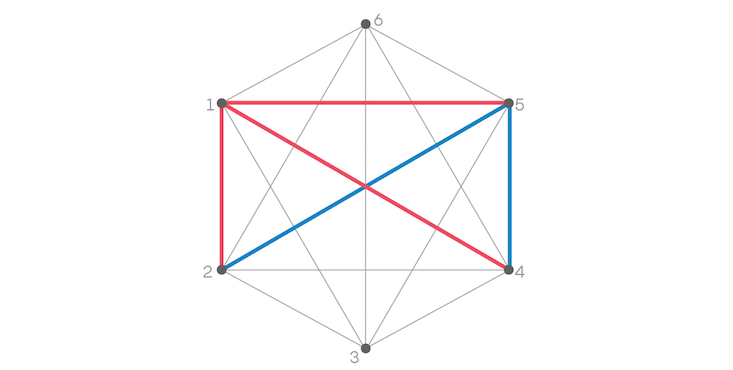
Lastly we have the relationship between Person 2 and Person 4. They either know each other or they don’t, rendering the edge between them red or blue. Either way, we’re compelled to create a triangle that’s all one color, and Ramsey’s theorem is confirmed.
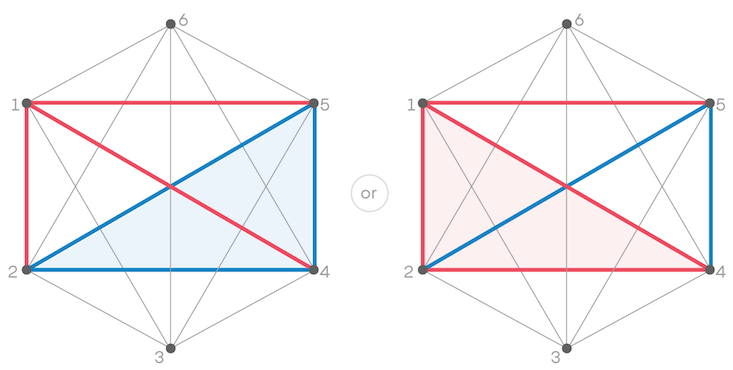
In larger graphs—cases with a million people, or many billion—Ramsey’s theorem guarantees that all points in some vast subset of the graph will be connected with lines of the same color. But how vast is “vast”? Mathematicians aren’t sure. In particular, they don’t know the minimum size a graph can be before we are guaranteed a subset of a given size (for all possible sizes). In this way, Ramsey’s theorem is like many tools we use every day—it’s useful, even if we don’t understand everything about how it works.
Kevin Hartnett is a senior writer at Quanta Magazine covering mathematics and computer science. His work has been collected in the “Best Writing on Mathematics” series in 2013 and 2016. From 2013-2016 he wrote “Brainiac,” a weekly column for the Boston Globe‘s Ideas section.
WATCH: Robbert Dijkgraaf, the director of the Institute for Advanced Study, on when we know mathematical unification is physically meaningful.