Chaos Makes the Multiverse Unnecessary

Scientists look around the universe and see amazing structure. There are objects and processes of fantastic complexity. Every action in our universe follows exact laws of nature that are perfectly expressed in a mathematical language. These laws of nature appear fine-tuned to bring about life, and in particular, intelligent life. What exactly are these laws of nature and how do we find them?

The universe is so structured and orderly that we compare it to the most complicated and exact contraptions of the age. In the 18th and 19th centuries, the universe was compared to a perfectly working clock or watch. Philosophers then discussed the Watchmaker. In the 20th and 21st centuries, the most complicated object is a computer. The universe is compared to a perfectly working supercomputer. Researchers ask how this computer got its programming.

How does one explain all this structure? Why do the laws seem so perfect for producing life and why are they expressed in such exact mathematical language? Is the universe really as structured as it seems?

One answer to some of these questions is Platonism (or its cousin Realism). This is the belief that the laws of nature are objective and have always existed. They possess an exact ideal form that exists in Plato’s realm. These laws are in perfect condition and they have formed the universe that we see around us. Not only do the laws of nature exist in this realm, but they live alongside all perfectly formed mathematics. This is supposed to help explain why the laws are written in the language of mathematics.

Platonism leaves a lot to be desired. The main problem is that Platonism is metaphysics, not science. However, even if we were to accept it as true, many questions remain. Why does this Platonic world have these laws, that bring intelligent life into the universe, rather than other laws? How was this Platonic attic set up? Why does our physical universe follow these ethereal rules? How do scientists and mathematicians get access to Plato’s little treasure chest of exact ideals?

The multiverse is another answer that has recently become quite fashionable. This theory is an attempt to explain why our universe has the life-giving laws that it does. One who believes in a multiverse maintains that our universe is just one of many universes. Each universe has its own set of rules and its own possible structures that come along with those rules. Physicists who push the multiverse theory believe that the laws in each universe are somewhat arbitrary. The reason we see structures fit for life in our universe is that we happen to live in one of very few universes that have such laws. While the multiverse explains some of the structure that we see, there are questions that are left open. Rather than asking why the universe has the structure it does, we can push the question back and ask why the multiverse has the structure it does. Another problem is that while the multiverse would answer some of the questions we posed if it existed, who says it actually exists? Since most believe that we have no contact with possible other universes, the question of the existence of the multiverse is essentially metaphysics.

It is almost a tautology: science predicts predictable phenomena.

There is another, more interesting, explanation for the structure of the laws of nature. Rather than saying that the universe is very structured, say that the universe is mostly chaotic and for the most part lacks structure. The reason why we see the structure we do is that scientists act like a sieve and focus only on those phenomena that have structure and are predictable. They do not take into account all phenomena; rather, they select those phenomena they can deal with.

Some people say that science studies all physical phenomena. This is simply not true. Who will win the next presidential election and move into the White House is a physical question that no hard scientists would venture to give an absolute prediction. Whether or not a computer will halt for a given input can be seen as a physical question and yet we learned from Alan Turing that this question cannot be answered. Scientists have classified the general textures and heights of different types of clouds, but, in general, are not at all interested in the exact shape of a cloud. Although the shape is a physical phenomenon, scientists don’t even attempt to study it. Science does not study all physical phenomena. Rather, science studies predictable physical phenomena. It is almost a tautology: science predicts predictable phenomena.

Scientists have described the criteria for which phenomena they decide to study: It is called symmetry. Symmetry is the property that despite something changing, there is some part of it that remains the same. When you say that a face has symmetry, you mean that if the left side is reflected and swapped with the right side, it will still look the same. When physicists use the word symmetry they are discussing collections of physical phenomena. A set of phenomena has symmetry if it is the same after some change. The most obvious example is symmetry of location. This means that if one performs the same experiment in two different places, the results should be the same. Symmetry of time means that the outcomes of experiments should not depend on when the experiment took place. And, there are many other types of symmetry.

The phenomena that are selected by scientists for study must have many different types of symmetry. When a physicist sees a lot of phenomena, she must first determine if these phenomena have symmetry. She performs experiments in different places and at different times. If she achieves the same results, she then studies them to find the underlying cause. In contrast, if her experiments failed to be symmetric, she would ignore them.

While scientists like Galileo and Newton recognized the symmetry in physical phenomena, the power of symmetry was first truly exploited by Albert Einstein. He postulated that the laws of physics should be the same even if the experimenter is moving close to the speed of light. With this symmetry in mind, he was able to compose the laws of special relativity. Einstein was the first to understand that symmetry was the defining characteristic of physics. Whatever has symmetry will have a law of nature. The rest is not part of science.

A little after Einstein showed the vital importance of symmetry for the scientific endeavor, Emmy Noether proved a powerful theorem that established a connection between symmetry and conservation laws. This is related to the constants of nature, which are central to modern physics. Again, if there is symmetry, then there will be conservation laws and constants. The physicist must be a sieve and study those phenomena that possess symmetry and allow those that do not possess symmetry to slip through her fingers.

We pick out those phenomena that satisfy the requirements of symmetry and predictability.

There are a few problems with this explanation of the structure found in the universe. For one, it seems that phenomena that we do select and that have laws of nature are exactly the phenomena that generate all the phenomena. The laws of particle physics, gravity, and quantum theory all have symmetries and are studied by physicists. All phenomena seem to come from these theories, even those that do not seem to have symmetry. So while it is beyond science to determine who the next president will be, that phenomena will be determined by sociology, which is determined by psychology, which is determined by neural biology which depends on chemistry which depends on particle physics and quantum mechanics. Determining the winner of an election is too complicated for the scientist to deal with, but the results of the election are generated by laws of physics that are part of science.

Despite this failing of our explanation for the structure of the laws of nature, we believe it is the best candidate for being the solution. It is one of the only solutions that does not invoke any metaphysical principle or the existence of a multitude of unseen universes. We do not have to look outside the universe to find a cause for the structure that we find in the universe. Rather, we look at how we are looking at phenomena.

Before we move on, we should point out that our solution has a property in common with the multiverse solution. We postulated that, for the most part, the universe is chaotic and there is not so much structure in it. We, however, focus only on the small amount of structure that there is. Similarly, one who believes in the multiverse believes that most of the multiverse lacks the structure to form intelligent life. It is only in a select few universes that we find complex structure. And we inhabitants of this complex universe are focused on that rare structure. Both solutions are about focusing on the small amount of structure in a chaotic whole.

A Hierarchy of Number Systems

This idea that we only see structure because we are selecting a subset of phenomena is novel and hard to wrap one’s head around. There is an analogous situation in mathematics that is much easier to understand. We will focus on one important example where one can see this selection process very clearly. First we need to take a little tour of several number systems and their properties.

Consider the real numbers. In the beginning of high school, the teacher draws the real number line on the board and says that these are all the numbers one will ever need. Given two real numbers, we know how to add, subtract, multiply, and divide them. They comprise a number system that is used in every aspect of science. The real numbers also have an important property: They are totally ordered. That means that given any two different real numbers, one is less than the other. Just think of the real number line: Given any two different points on the line, one will be to the right of the other. This property is so obvious that it is barely mentioned.

While the real numbers seem like a complete picture, the story does not end there. Already in the 16th century, mathematicians started looking at more complicated number systems. They began working with an “imaginary” number i that has the property that its square is -1. This is in stark contrast to any real number whose square is never negative. They defined an imaginary number as the product of a real number and i. Mathematicians went on to define a complex number that is the sum of a real number and an imaginary number. If r₁ and r₂ are real numbers, then r₁+r₂i is a complex number. Since a complex number is built from two real numbers, we usually draw all of them in a two-dimensional plane. The real number line sits in the complex plane. This corresponds to the fact that every real number, r₁, can be seen as the complex number r₁+0i (that is, itself with zero complex component).

We know how to add, subtract, multiply, and divide complex numbers. However, there is one property that is different about the complex numbers. In contrast to the real numbers, the complex numbers are not totally ordered. Given two complex numbers, say 3 + 7.2i and 6 – 4i, can we tell which one is more and which one is less? There is no obvious answer. (In fact, one can totally order the complex numbers but the ordering will not respect the multiplication of complex numbers.) The fact that the complex numbers are not totally ordered means that we lose structure when we go from the real numbers to the complex numbers.

The story is not over with the complex numbers. Just as one can construct the complex numbers from pairs of real numbers, so too can one construct the quaternions from pairs of complex numbers. Let c₁ = r₁ + r₂i and c₂ = r₃ + r₄i be complex numbers; then we can construct a quaternion as q = c₁ + c₂j where j is a special number. It turns out that every quaternion can be written as

r₁ + r₂i + r₃j + r₄k,

where i, j, and k are all special numbers similar to complex numbers (they are defined by ijk = -1 = i² = j² = k²). So while the complex numbers are comprised of two real numbers, the quaternions are comprised of four real numbers. Every complex number r₁ + r₂i can be seen as a special type of quaternion: r₁+ r₂i + 0j + 0k. We can think of the quaternions as a four-dimensional space that has the complex numbers as a two-dimensional subset of it. We humans have a hard time visualizing such higher-dimensional spaces.

The quaternions are a full-fledged number system. They can be added, subtracted, multiplied, and divided with ease. Like the complex numbers, they fail to be totally ordered. But they have even less structure than the complex numbers. While the multiplication of complex numbers is commutative, that is, for all complex numbers c₁ and c₂ we have that c₁c₂ = c₂c₁, this is not true for all quaternions. This means there are quaternions q₁ and q₂ such that q₁q₂ is different than q₂q₁.  

Rather than looking at the real numbers as central and the octonions as strange larger number systems, think of the octonions as fundamental and all the other number systems as just special subsets of octonions.

This process of doubling a number system with a new special number is called the “Cayley–Dickson construction,” named after the mathematicians Arthur Cayley and Leonard Eugene Dickson. Given a certain type of number system, one gets another number system that is twice the dimension of the original system. The new system that one develops has less structure (i.e. fewer axioms) than the starting system.

If we apply the Cayley–Dickson construction to the quaternions, we get the number system called the octonions. This is an eight-dimensional number system. That means that each of the octonions can be written with eight real numbers as

r₁+ r₂i + r₃j + r₄k +r₅l + r₆m + r₇n + r₈p.

Although it is slightly complicated, it is known how to add, subtract, multiply, and divide octonions. Every quaternion can be written as a special type of octonion in which the last four coefficients are zero.

Like the quaternions, the octonions are neither totally ordered nor commutative. However, the octonions also fail to be associative. In detail, all the number systems that we have so far discussed possess the associative property. This means that for any three elements, a, b, and c, the two ways of multiplying them, a(bc) and (ab)c, are equal. However, the octonions fail to be associative. That is, there exists octonions o₁, o₂ and o₃ such that o₁(o₂o₃) ≠ (o₁o₂)o₃.

We can go on with this doubling and get an even larger, 16-dimensional number system called the sedenions. In order to describe a sedonion, one would have to give 16 real numbers. Octonions are a special type of sedonion: their last eight coefficients are all zero. But researchers steer clear of sedenions because they lose an important property. While one can add, subtract, and multiply sedenions, there is no way to nicely divide them. Most physicists think this is beyond the pale and “just” mathematics. Even mathematicians find sedenions hard to deal with. One can go on to formulate 32-dimensional number systems and 64-dimensional number systems, and so on. But they are usually not discussed because, as of now, they do not have many applications. We will concentrate on the octonions. A summary of all the number systems can be seen in this Venn diagram:

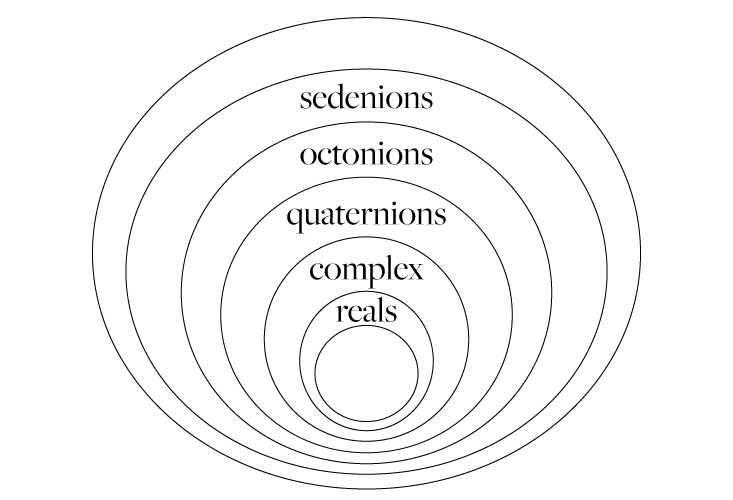
Let us discuss the applicability of these number systems. The real numbers are used in every aspect of physics. All quantities, measurements, and lengths of physical objects or processes are given as real numbers. Although complex numbers were formulated by mathematicians to help solve equations (i is the solution to the equation x² = -1), physicists started using complex numbers to discuss waves in the middle of the 19th century. In the 20th century, complex numbers became fundamental for the study of quantum mechanics. By now, the role of complex numbers is very important in many different branches of physics. The quaternions show up in physics but are not a major player. The octonions, the sedenions, and the larger number systems rarely arise in the physics literature.

The Laws of Mathematics That We Find

The usual view of these number systems is to think that the real numbers are fundamental while the complex, quaternions, and octonions are strange larger sets that keep mathematicians and some physicists busy. The larger number systems seem unimportant and less interesting.

Let us turn this view on its head. Rather than looking at the real numbers as central and the octonions as strange larger number systems, think of the octonions as fundamental and all the other number systems as just special subsets of octonions. The only number system that really exists is the octonions. To paraphrase Leopold Kronecker, “God made the octonions, all else is the work of man.” The octonions contain every number that we will ever need. (And, as we stated earlier, we can do the same trick with the sedenions and even the 64-dimensional number system. We shall fix our ideas with the octonions.)

Let us explore how we can derive all the properties of the number systems that we are familiar with. Although the multiplication in the octonions is not associative, if one wants an associative multiplication, one can look at a special subset of the octonions. (We are using the word “subset” but we need a special type of subset that respects the operations of the number system. Such subsets are called “subgroups,” “subfields,” or “sub-normed-division-algebras.”) So if one selects the subset of all octonions of the form

r₁+ r₂i + r₃j + r₄k + 0l + 0m + 0n + 0p,

then the multiplication will be associative (like the quaternions). If one further looks at all the octonions of the form

r₁+ r₂i + 0j + 0k + 0l + 0m + 0n + 0p,

then the multiplication will be commutative (like the complex numbers). If one further selects all the octonions of the form

r₁ + 0i + 0j + 0k + 0l + 0m + 0n + 0p,

then they will have a totally ordered number system. All the axioms that one wants satisfied are found “sitting inside” the octonions.

This is not strange. Whenever we have a structure, we can focus on a subset of special elements that satisfies certain properties. Take, for example, any group. We can go through the elements of the group and pick out those X such that, for all elements Y, we have that XY = YX. This subset is a commutative (abelian) group. That is, it is a fact that in any group there is a subset that is a commutative group. We simply select those parts that satisfy the axiom and ignore (“bracket out”) those that do not. The point we are making is that if a system has a certain structure, special subsets of that system will satisfy more axioms than the starting system.

This is similar to what we are doing in physics. We do not look at all phenomena. Rather, we pick out those phenomena that satisfy the requirements of symmetry and predictability. In mathematics, we describe the subset with the axiom that describes it. In physics, we describe the selected subset of phenomena with a law of nature.

We can describe the analogy we made with the following diagram:

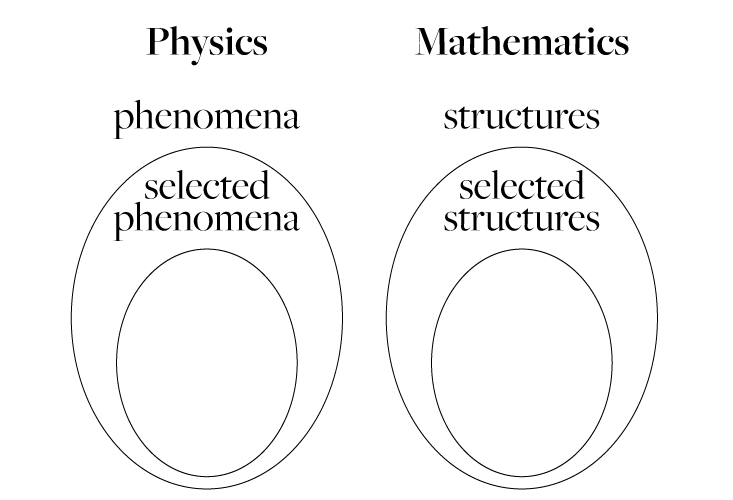
Notice that the mathematics for a subset chosen to satisfy an axiom is easier than the mathematics for the whole set. This is because mathematicians work with axioms. They prove theorems and make models using axioms. When such axioms are missing, the mathematics gets more complicated or impossible.

Following our analogy, a subset of phenomena is easier to describe with a law of nature stated in mathematics. In contrast, when we look at the larger set of phenomena, it is harder to find that law of nature and the mathematics would be more complicated or impossible.

Working in Tandem and Going Forward

There is an important analogy between physics and mathematics. In both fields, if we do not look at the entirety of a system, but rather look at special subsets of the system, we see more structure. In physics we select certain phenomena (the ones that have a type of symmetry) and ignore the rest. In mathematics we are looking at certain subsets of structures and ignore the rest. These two bracketing operations work hand in hand.

The job of physics is to formulate a function from the collection of observed physical phenomena to mathematical structure:

observed physical phenomena → mathematical structure.

That is, we have to give mathematical structure to the world we observe. As physics advances and we try to understand more and more observed physical phenomena, we need larger and larger classes of mathematics. In terms of this function, if we are to enlarge the input of the function, we need to enlarge the output of the function.

There are many examples of this broadening of physics and mathematics.

When physicists started working with quantum mechanics they realized that the totally ordered real numbers are too restrictive for their needs. They required a number system with fewer axioms. They found the complex numbers.

When Albert Einstein wanted to describe general relativity, he realized that the mathematical structure of Euclidean space with its axiom of flatness (Euclid’s fifth axiom) was too restrictive. He needed curved, non-Euclidian space to describe the spacetime of general relativity.

In quantum mechanics it is known that for some systems, if we first measure X and then Y, we will get different results than first measuring Y and then measuring X. In order to describe this situation mathematically, one needed to leave the nice world of commutativity. They required the larger class of structures where commutativity is not assumed.

When Boltzmann and Gibbs started talking about statistical mechanics, they realized that laws they were coming up with were no longer deterministic. Outcomes of experiments no longer either happen (p(X) = 1) or do not happen (p(X) = 0). Rather, with statistical mechanics one needs probability theory. The chance of a certain outcome of an experiment is a probability (p(X)) is an element of the infinite set [0,1] rather than the restrictive finite subset {0,1}).

When scientists started talking about the logic of quantum events, they realized that the usual logic, which is distributive, is too restrictive. They needed to formulate the larger class of logics in which the distributive axiom does not necessarily hold true. This is now called quantum logic.

Paul A.M. Dirac understood this loosening of axioms about 85 years ago when he wrote the following:

The steady progress of physics requires for its theoretical formulation a mathematics which get continually more advanced. This is only natural and to be expected. What however was not expected by the scientific workers of the last century was the particular form that the line of advancement of mathematics would take, namely it was expected that mathematics would get more and more complicated, but would rest on a permanent basis of axioms and definitions, while actually the modern physical developments have required a mathematics that continually shifts its foundation and gets more abstract. Non-Euclidean geometry and noncommutative algebra, which were at one time were considered to be purely fictions of the mind and pastimes of logical thinkers, have now been found to be very necessary for the description of general facts of the physical world. It seems likely that this process of increasing abstraction will continue in the future and the advance in physics is to be associated with continual modification and generalisation of the axioms at the base of mathematics rather than with a logical development of any one mathematical scheme on a fixed foundation.¹

As physics progresses and we become aware of more and more physical phenomena, larger and larger classes of mathematical structures are needed and we get them by looking at fewer and fewer axioms. Dirac calls these mathematical structures with fewer axioms “increasing abstraction” and “generalisations of the axioms.” There is no doubt that if Dirac lived now, he would talk about the rise of octonions and even the sedenions within the needed number systems.

In order to describe more phenomena, we will need larger and larger classes of mathematical structures and hence fewer and fewer axioms. What is the logical conclusion to this trend? How far can this go? Physics wants to describe more and more phenomena in our universe. Let us say we were interested in describing all phenomena in our universe. What type of mathematics would we need? How many axioms would be needed for mathematical structure to describe all the phenomena? Of course, it is hard to predict, but it is even harder not to speculate. One possible conclusion would be that if we look at the universe in totality and not bracket any subset of phenomena, the mathematics we would need would have no axioms at all. That is, the universe in totality is devoid of structure and needs no axioms to describe it. Total lawlessness! The mathematics are just plain sets without structure. This would finally eliminate all metaphysics when dealing with the laws of nature and mathematical structure. It is only the way we look at the universe that gives us the illusion of structure.

With this view of physics we come to even more profound questions. These are the future projects of science. If the structure that we see is illusory and comes about from the way we look at certain phenomena, then why do we see this illusion? Instead of looking at the laws of nature that are formulated by scientists, we have to look at scientists and the way they pick out (subsets of phenomena and their concomitant) laws of nature. What is it about human beings that renders us so good at being sieves? Rather than looking at the universe, we should look at the way we look at the universe.

I am grateful to Jim Cox, Karen Kletter, Avi Rabinowitz, and Karl Svozil for many helpful conversations.

Noson S. Yanofsky has a Ph.D. in mathematics from The Graduate Center of The City University of New York. He is a professor of computer science at Brooklyn College of The City University of New York. In addition to writing research papers he has co-authored Quantum Computing for Computer Scientists and authored The Outer Limits of Reason: What Science, Mathematics, and Logic Cannot Tell Us. Noson lives in Brooklyn with his wife and four children.

References

1. Dirac, P.A.M. Quantised singularities in the electromagnetic field. Proceedings of the Royal Society 133, 60-72, (1931).

Additional Reading

Dray, T. & Manogue, C.A. The Geometry of the Octonions World Scientific Publishing Company, Singapore (2015).

Eddington, A.S. The Philosophy of Physical Science Cambridge University Press, New York, NY (1939).

van Fraassen, B.C. Laws and Symmetry Oxford University Press, New York, NY (1989).

Greene, B. The Hidden Reality: Parallel Universes and the Deep Laws of the Cosmos Knopf, New York, NY (2011).

Stenger, V.J. The Comprehensible Cosmos: Where Do the Laws of Physics Come From? Prometheus Books, Amherst, NY (2006).

Tegmark, M. Our Mathematical Universe: My Quest for the Ultimate Nature of Reality Knopf, New York, NY (2014).

Yanofsky, N.S. The Outer Limits of Reason: What Science, Mathematics, and Logic Cannot Tell Us MIT Press, Cambridge, MA (2013).

Lead image collage credits: Marina Sun / Shutterstock; Pixabay

Get the Nautilus newsletter

Cutting-edge science, unraveled by the very brightest living thinkers.

NL – In Page Mobile

Email: *

Captcha

Sign up for free