Like most people, my high-school training in mathematics involved next-to-no history, barely touching on the names of a few mathematicians, like Pythagoras, and their theorems. I graduated only vaguely aware that geometry came from ancient Greece and algebra came from the Babylonians.
A decade later, as a graduate researcher of chemical engineering at the University of Wisconsin, I realized that by not knowing anything about the origins of these branches of mathematics, I was missing out on something extremely important. I began rummaging through this history to see their elaborate unfolding myself and, to my surprise, found that geometry was far more developed than algebra for a long time: Geometric solutions to many mathematical problems were discovered more than a millennium before their algebraic equivalents.
This is the story of how an ancient, arbitrary rule of Greek thinkers obstructed algebra’s progress for more than a thousand years, and how a peculiar loophole allowed geometry to anticipate mathematics far ahead of its time.
Ancient Greeks, up until Greece fell to Rome in the 2nd-century BCE, practiced geometry to explore the relationships among points, lines, angles, and shapes. “The so-called Pythagoreans,” says Aristotle, “who were the first to take up mathematics, not only advanced this subject, but saturated with it, they fancied that the principles of mathematics were the principles of all things.” In particular, they treated “numbers” with religious reverence and thought they had to be whole values—like 6 and 13—pure, simple, and elegant. They also recognized that “ratios” could be formed between whole numbers, like 2/3, 8/9, 243/256, and so on. If a value wasn’t whole, or couldn’t be represented as a ratio of whole numbers, then it wasn’t a true number to them.
Pointing out that geometry actually needed other kinds of numbers was a kind of blasphemy. Legend has it that a Pythagorean cult member named Hippasus was thrown from a ship, condemned to drown at the bottom of the sea, for having proved what was contrary to Pythagorean dogma: That numbers can be imperfect. Certain lengths in isosceles right triangles, regular pentagons, and regular dodecahedrons (shown in dashed red lines below) couldn’t be represented as ratios of whole numbers when compared against the figures’ other lengths.
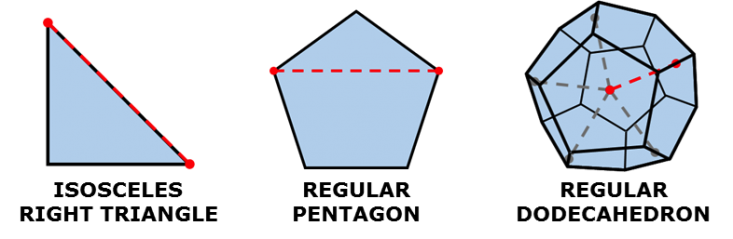
The Pythagoreans and later Greek scholars had to confront the reality of these lengths somehow. But rather than make room in their understanding for numbers that weren’t whole, or weren’t ratios of whole numbers, they—in almost Orwellian fashion—instead decided that such lengths were “ἄλογος” (pronounced “al’-og-os”), meaning both “not a ratio” and “not to be spoken,” writes Edna E. Kramer in The Nature and Growth of Modern Mathematics. In other words, they avoided heresy by forbidding themselves from thinking of those lengths as numbers, which Kramer called the “Pythagorean predicament”—they had “no numbers available for the exact measurement of certain line segments.” Today we describe these lengths as “irrational,” which means “not a ratio,” but also “not based on clear thinking,” reflecting the ancient stigma.
Though these numbers were “not to be spoken,” Greek scholars were still perfectly content to geometrically construct—or in other words draw—all manner of irrational lengths, just so long as those lengths were not represented in numeric form, something they viewed, says Kramer, with “dread.” This loophole allowed geometry to keep advancing, but the “not a number” fallacy prevented Greek algebraists of the time from taking parallel strides. For them, numbers had to be spoken, or at least written out, since algebra was still practiced rhetorically, writes Kramer. “Results were obtained by means of verbal argument, without abbreviations or symbols of any kind.” They may not have ignored the Pythagorean rule because they were fearful of joining Hippasus at the bottom of the Mediterranean Sea.
In his Elements, an ancient Greek geometry textbook written around 300 BCE, Euclid includes a geometric proof of how to produce a Golden Rectangle, which includes an irrational length ratio. Successful as these geometric methods—proofs by dissection and rearrangement—were, they were difficult to think up, follow, and apply to natural phenomena. Then something easier and more applicable came along: medieval Islamic algebra.
In the early 9th-century CE, Caliph Al-Ma’mun of the Abbasid Caliphate built an intellectual center that, up until its destruction by the Mongols in the mid-13th-century CE, rivaled the ancient library at Alexandria. At the House of Wisdom in Medieval Baghdad, Muslim scholars gathered and further developed the mathematical ideas of their neighboring civilizations—in particular the Byzantine (East Roman) Empire and the Tripartite Empires of Northern India—and, free from the Pythagorean dogma, began to address irrational numbers algebraically.
For example, a commentary on Euclid’s Elements by the 9th-century Persian mathematician Al-Mahani is the first known algebraic treatment of irrational lengths found in geometry that can be considered solutions to the quadratic equation. Algebraists could finally solve the same problems Greek geometers had been solving for centuries, but with methods that were sleeker, faster, and more pragmatic.
So, the next time algebra pops into your life, view it as a hard-won victory.
Robert Coolman is a freelance science writer based in Madison, WI. Follow him on Twitter @PrimeViridian.
Lead image: Pythagoreans celebrate sunrise (1869), a painting by Fyodor Bronnikov (1827–1902). Wikicommons


























