Justin Trudeau, the Canadian prime minister, certainly raised the profile of quantum computing a few notches last year, when he gamely—if vaguely1—described it for a press conference. But we’ve heard a lot about quantum computers in the past few years, as Google, I.B.M., and N.A.S.A., as well as many, many universities, have all been working on, or putting money into, quantum computers for various ends. The N.S.A., for instance, as the Snowden documents revealed, wants to build one for codebreaking, and it seems to be a common belief that if a full-scale, practical quantum computer is built, it could be really useful in that regard. A recent New Yorker article, for example, stated that a quantum computer “would, on its first day of operation, be capable of cracking the Internet’s most widely used codes.” But maybe they won’t be as useful as we have been led to believe.
Some are looking at ways to “fight quantum with quantum”—but there is another (and cheaper) option.
Quantum computation is based on the superposition principle of quantum physics. Bits in a normal computer are either 0 or 1. Quantum physics allows bits to be in a superposition of 0 and 1, in the same way Schrödinger’s cat can be in a superposition of “alive” and “dead.” This sometimes lets quantum computers explore possibilities more quickly than normal computers. For a general search problem, such as trying to find the key to a secret code by trying all of them, quantum computers are expected to have quadratic speed-up. For example, the Advanced Encryption Standard, approved by the United States government, has up to 2256—or about a 1 followed by 77 zeros—keys. A quantum computer could make that same search as if there were only 2128 keys—about a 3 followed by 38 zeros. On the one hand, that’s a lot faster. On the other hand, it’s still an awful lot of searching to do.
But there’s another type of cryptography, called public-key cryptography, which was invented in the 1970s. As the name suggests, these are systems where two people can agree on a key, or part of a key, by exchanging only public information. This is incredibly useful in modern electronic commerce—if you want to send your credit card number safely over the Internet to Amazon, for instance, you don’t want to have to drive to their headquarters to have a secret meeting first. Public-key systems rely on the fact that some mathematical processes seem to be one-way—they are easy to do but difficult to undo. For example, for you to take two large whole numbers and multiply them is relatively easy. But for someone to take the result and factor it into the original numbers seems much harder. This particular one-way function is used in RSA cryptography, one of the most popular public-key systems.
Unfortunately for RSA, not all one-way functions are created equal. The factoring problem falls into a category known as “hidden subgroup problems.” A group is a particular type of mathematical structure and a hidden subgroup is another structure inside it unknown to the codebreaker—in the factoring example, the product produces the group and the unknown factors produce the hidden subgroup. On hidden subgroup problems, quantum computers are predicted to get exponential speed-up. Factoring is faster than searching to begin with, so an ordinary computer could factor a number of size 215360 in the time it takes to search 2256 keys. But a quantum computer could factor that same number in more like the time it takes to search 20,000 keys. That’s an enormous speed-up. It would pretty much destroy RSA, and the situation is similar with all of the other public-key systems currently in common use.
That would be a big shake-up for public-key cryptography, but cryptographers aren’t just giving up. Some are looking at ways to “fight quantum with quantum”—but there is another (and cheaper) option. Research is also being done into what is often called post-quantum cryptography, although a more precise name might be quantum-resistant cryptography. These are systems running on ordinary computers but based on problems that are not in the hidden subgroup category. These problems include solving systems of multivariable polynomials, finding the shortest distance from a point to an n-dimensional skewed grid of other points, and finding the closest bit string to a set of other bit strings.
For example, if Alice wants to send Bob a message, she could identify it with a point in Bob’s n-dimensional grid and then add some “noise” to it by moving it off the grid a small amount. If n is very large and the angles in the grid are skewed—very far from right angles—it seems difficult for Eve the Eavesdropper to figure out Alice’s original point, and a quantum computer doesn’t seem to help much. But if Bob (and only Bob) has a different set of lines drawn through the same points, but with angles closer to 90 degrees, then he has a “trap door” which allows him to recover the point and the message. Variations on this idea are known as lattice-based cryptography, and are some of the front-runners for post-quantum use.
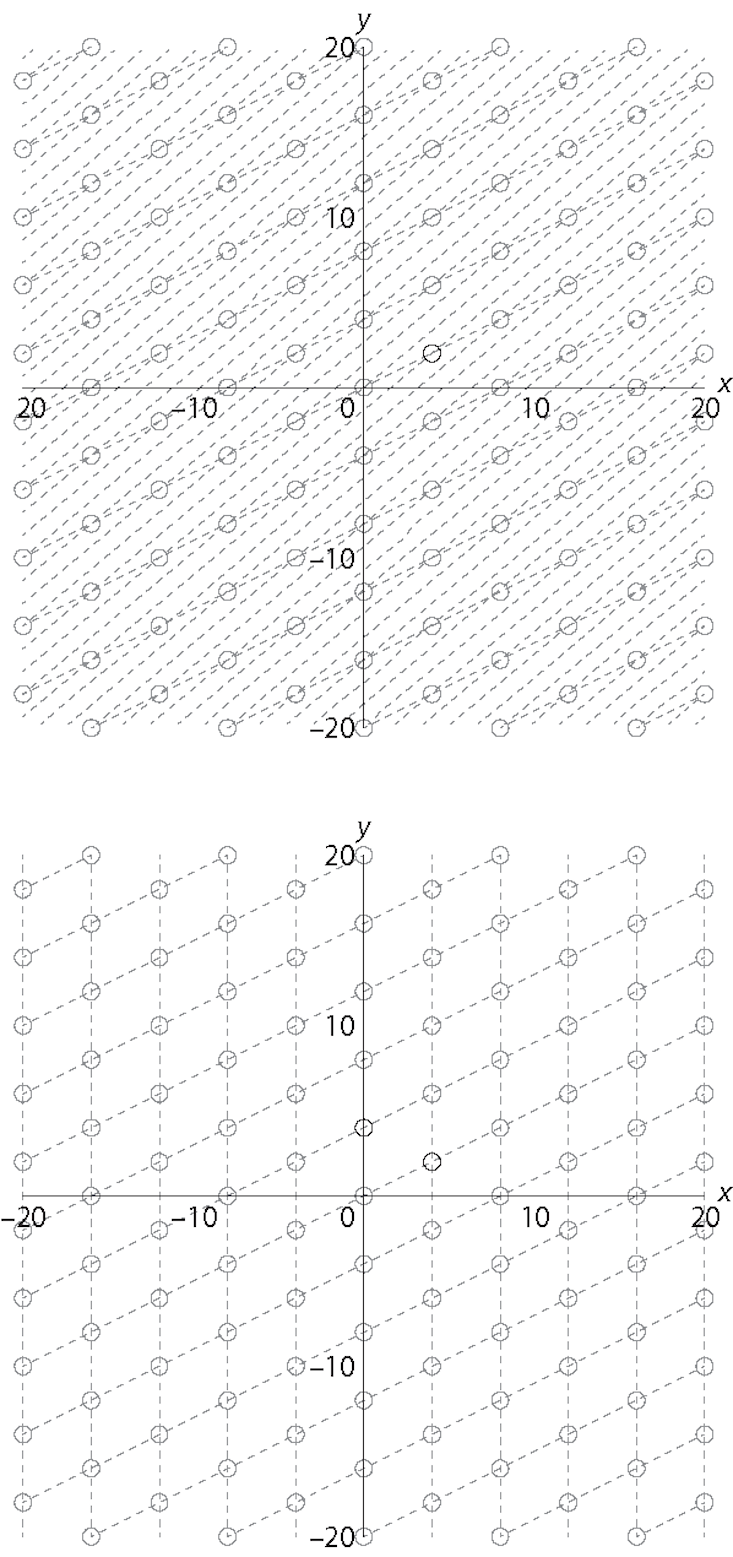
The methods of post-quantum cryptography have not been used in the past because they are less efficient than current public-key methods, but they are getting better. In August 2015, the N.S.A. announced that it was planning to introduce a list of approved cryptography methods that would resist quantum computers. In April 2016, the National Institute of Standards and Technology followed suit, starting a public vetting process lasting 4 to 6 years.
That’s not an unreasonable amount of time to need in order to be sure that a cryptographic method is really secure. For example, in 2014 in was revealed that researchers at the Government Communications Headquarters, more or less the British equivalent of the N.S.A., had developed a lattice-based cryptographic algorithm that at first appeared to be quantum-resistant. After several years of study, however, the researchers discovered how to use tools from the field of algebraic number theory to identify a hidden lattice which would reveal the trap door. The problem they were using fell into the hidden subgroup category after all.
Four to six years is also not an unreasonable amount of time to wait for a new cryptographic standard. Government agencies are concerned about protecting data that might have to remain secure for decades into the future, so they are preparing now for computers that could still be 10 or 20 years into the future.
If you are worried about quantum criminals getting your credit card number off of the Internet, you can breathe a little easier. When quantum computers come, cryptographers expect to be ready for them. And you will be able to keep shopping safely without buying your own quantum computer, although I’m sure Amazon will be happy to sell you one.
Joshua Holden is professor of mathematics at the Rose-Hulman Institute of Technology and the author of The Mathematics of Secrets: Cryptography from Caesar Ciphers to Digital Encryption.
Note
1. See “Grading Trudeau on quantum computing,” from Scott Aaronson’s blog, Shtetl-Optimized.
WATCH: The theoretical computer scientist Scott Aaronson on his beef with D-Wave, a quantum computer company.

Image credit: Oak Ridge National Laboratory / Flickr