Mathematicians long wondered whether it’s possible to express the number 33 as the sum of three cubes—that is, whether the equation 33 = x³+ y³+ z³ has a solution. They knew that 29 could be written as 3³ + 1³ + 1³, for instance, whereas 32 is not expressible as the sum of three integers each raised to the third power. But the case of 33 went unsolved for 64 years.
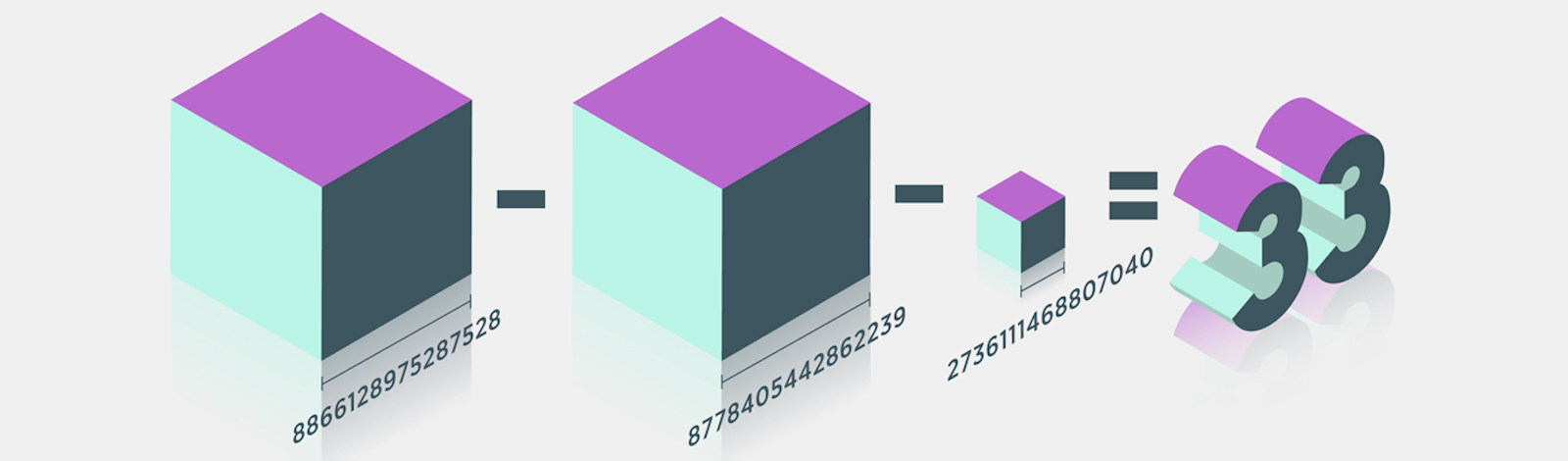
Now, Andrew Booker, a mathematician at the University of Bristol, has finally cracked it: He discovered that (8,866,128,975,287,528)³ + (–8,778,405,442,862,239)³ + (–2,736,111,468,807,040)³ = 33.
Booker found this odd trio of 16-digit integers by devising a new search algorithm to sift them out of quadrillions of possibilities. The algorithm ran on a university supercomputer for three weeks straight. (He says he thought it would take six months, but a solution “popped out before I expected it.”) When the news of his solution hit the Internet earlier this month, fellow number theorists and math enthusiasts were feverish with excitement. According to a Numberphile video about the discovery, Booker himself literally jumped for joy in his office when he found out.
“He has found a genuinely more efficient way of locating the solutions.”
Why such elation? Part of it is the sheer difficulty of finding such a solution. Since 1955, mathematicians have used the most powerful computers they can get their hands on to search the number line for trios of integers that satisfy the “sum of three cubes” equation k = x³ + y³ + z³, where k is a whole number. Sometimes solutions are easy, as with k = 29; other times, a solution is known not to exist, as with all whole numbers that leave behind a remainder of 4 or 5 when divided by 9, such as the number 32.
But usually, solutions are “nontrivial.” In these cases, the trio of cubed integers—like (114,844,365)³ + (110,902,301)³ + (–142,254,840)³, which equals 26—looks more like a lottery ticket than anything with predictable structure. For now, the only way for number theorists to discover such solutions is to play the mathematical “lottery” over and over, using the brute force of computer-assisted search to try different combinations of cubed integers, and hope for a “win.”
But even with increasingly powerful computers and more efficient algorithms thrown at the problem, some whole numbers have stubbornly refused to yield any winning tickets. And 33 was an especially stubborn case: Until Booker found his solution, it was one of only two integers left below 100 (excluding the ones for which solutions definitely don’t exist) that still couldn’t be expressed as a sum of three cubes. With 33 out of the way, the only one left is 42.
The reason it took so long to find a solution for 33 is that searching far enough up the number line—all the way to 1016, or 10 quadrillion, and just as far down into the negative integers—for the right numerical trio was computationally impractical until Booker devised his algorithm. “He has not just run this thing on a bigger computer compared to the computers 10 years ago—he has found a genuinely more efficient way of locating the solutions,” said Tim Browning, a number theorist at the Institute of Science and Technology Austria.
Previous algorithms “didn’t know what they were looking for,” Booker explained; they could efficiently search a given range of integers for solutions to k = x³ + y³ + z³ for any whole number k, but they weren’t able to target a specific one, like k = 33. Booker’s algorithm could, and thus it works “maybe 20 times faster, in practical terms,” he said, than algorithms that take an untargeted approach.
With 33’s winning ticket now in hand, Booker plans to look next for a solution for 42. (He already determined that none exist in the 10-quadrillion range; he’ll have to look further out on the number line, to at least 1017.) But even when he or another number theorist has identified sum-of-three-cubes solutions for every eligible integer up to 100, they’ll then face 11 more “stubborn” integers without sum-of-three-cubes solutions between 101 and 1,000, and an infinitude of them beyond that. What’s more, Booker and other experts say, each new solution found for one of these holdouts sheds no theoretical light on where, or how, to find the next one. “I don’t think these are sufficiently interesting research goals in their own right to justify large amounts of money to arbitrarily hog a supercomputer,” Booker said.
So why bother with 33 or 42 at all?
What is “sufficiently interesting,” Booker explained, is that each newfound solution is “a tool for helping you decide what’s true” about the sum-of-three-cubes problem itself. That problem, stated as k = x³ + y³ + z³, is what number theorists call a Diophantine equation—a kind of algebraic structure whose properties have fascinated mathematicians for millennia. “They’re rich enough to encode [other mathematical] statements that have nothing to do with Diophantine equations,” said Browning. “They’re rich enough to simulate computers.”
Diophantine equations are polynomial equations whose unknown variables must take integer values. Their basic properties can stymie number theorists. For instance, no mathematical method exists that can reliably tell whether any given Diophantine equation has solutions. According to Booker, the sum-of-three-cubes problem “is one of the simplest” of these thorny Diophantine equations. “It’s right at the frontier of what we can handle,” Browning added.
For that reason, number theorists are eager to understand anything they can about sums of three cubes. A major result would be to prove the conjecture that k = x³ + y³ + z³ has infinitely many solutions for every whole number k, except those k that have a remainder of 4 or 5 after being divided by 9. The tools devised for such a proof might pry open the logic of the problem, or apply to other Diophantine equations. Results like Booker’s for 33 offer support for this conjecture, giving number theorists more confidence that it’s a proof worth pursuing. Indeed, every time number theorists have looked further up the number line with their search algorithms—for example, by extending out to 1014 in 2009, to 1015 in 2016, and now to 1016 in 2019—new solutions for previously stubborn integers have reliably been found, knocking out possible counterexamples to the conjecture.
“All of these things are kind of an accumulation of data,” Browning said. He noted that Booker’s new solution for 33 “is not going to change the course of mathematical research in this area. But it’s gratifying to see that things are falling as they should.”
John Pavlus is a writer and filmmaker whose work has appeared in Scientific American, Bloomberg Businessweek, and The Best American Science and Nature Writing series. He lives in Portland, Oregon.
Lead art credit: Lucy Reading-Ikkanda / Quanta Magazine
Reprinted with permission from Quanta Magazine’s Abstractions blog.