Imaginary numbers are not imaginary at all. The truth is, they have had far more impact on our lives than anything truly imaginary ever could. Without imaginary numbers, and the vital role they played in putting electricity into homes, factories, and internet server-farms, the modern world would not exist. Students who might complain to their math teacher that there’s no point in anyone learning how to use imaginary numbers would have to put down their phone, turn off their music, and pull the wires out of their broadband router. But perhaps we should start with an explanation of what an imaginary number is.
We know by now how to square a number (multiply it by itself), and we know that negative numbers make a positive number when squared; a minus times a minus is a plus, remember? So (–2) × (–2) = 4. We also know that taking a square root is the inverse of squaring. So the possible square roots of 4 are 2 and –2. The imaginary number arises from asking what the square root of –4 would be.
What we’re discovering here is not some deep mystery about the universe.
Surely the question is meaningless? If you square a number, whether positive or negative, the answer is positive. So you can’t do the inverse operation if you start with a negative number. That’s certainly what Heron of Alexandria seemed to think. Heron was the Egyptian architect whose mathematical tricks, written in Stereometrica, gave us the dome of the Hagia Sophia. In the same volume, he showed how to calculate the volume of a truncated square pyramid; that is, a pyramid with the top chopped off. His solution for one example involved subtracting 288 from 225 and finding the square root of the result. The result, though, is a negative number: –63. So the answer would be found via √–63.
For some reason—whether a sense that there was some mistake, or someone copied something down wrong, or because it was so absurd—the manuscripts we have show that Heron ignored the minus sign and gave the answer as √63 instead.
The square roots of negative numbers are what we now call imaginary numbers. The first person to suggest that they shouldn’t be ignored was the 16th-century Italian astrologer Jerome Cardano, who was embarked on a grand project: a book detailing all of the algebraic knowledge of his times. While working out cubic equations, he stopped and stared at the issue. At first, he called them “impossible cases.” In his 1545 book on algebra, The Great Art, he gave the example of trying to divide 10 into two numbers that multiply together to make 40. In the process of finding those numbers, you come across 5 + √–15.
Cardano didn’t shy away from this unexpected encounter. In fact, he even jotted down a few thoughts about it. However, he wrote in Latin, and translators argue about what he actually meant. For some, he calls it a “false position.” For others, it’s a “fictitious” number. Still others say he characterizes the situation as “impossible” to solve. One of his further comments on how to proceed in such a situation is translated as “putting aside the mental tortures” and as “the imaginary parts being lost.” Elsewhere he refers to this as “arithmetic subtlety, the end of which … is as refined as it is useless.” He says it “truly is sophisticated … one cannot carry out the other operations one can in the case of a pure negative.” By pure negative, he means a standard negative number, something like –4. He was happy with negative numbers and wrote that “√9 is either +3 or –3, for a plus [times a plus] or a minus times a minus yields a plus.” And then he continued, “√–9 is neither +3 or –3 but is some recondite third sort of thing.” Cardano clearly thought the square roots of negative numbers were something abstruse and abstract, but at the same time he knew they were something—and something that a mathematician should engage with. The task wasn’t for him, though; none of Cardano’s subsequent writings mention the square roots of negative numbers. He left it to his fellow countryman, Rafael Bombelli, to address them a couple of decades or so later.
In what he called a “wild thought,” Bombelli suggested in 1572 that the two terms in 5 + √–15 could be treated as two separate things. “The whole matter seemed to rest on sophistry rather than truth,” he said, but he did it anyway. And we still do it today because it works.
A full mathematical description of nature requires imaginary numbers to exist.
Bombelli’s two separate things were what we now call real numbers and imaginary numbers. The combination of the two is known as a “complex number” (it’s complex as in “military-industrial complex,” speaking of combination—of real and imaginary parts—rather than complication). But let’s be clear. If there’s one thing we’ve learned in our time revisiting mathematics, it’s that all numbers are imaginary. They are simply a notation that helps with the concept of “how many.” So applying the name “imaginary numbers” to the square roots of negative numbers is pejorative and unhelpful.
That said, we should acknowledge a distinction. What mathematicians call “real” numbers are the numbers you’re more familiar with. The “two” in two apples; the 3.14… in pi; the fraction. And just as positive numbers are in a sense complemented by negative numbers, what we call real numbers are complemented by what we now have to call imaginary numbers. Think of them as yin and yang, or heads and tails. And certainly not as actually imaginary.
Bombelli, in his wild thought, demonstrated that this new tribe of numbers have a role to play in the real world. He set out to solve a cubic equation that Cardano had given up on: x3 = 15x + 4. Cardano’s solution required him to deal with an expression that contained the square root of –121, and he just didn’t know where to go with it. Bombelli, on the other hand, thought he might try applying normal rules of arithmetic to the square root. So, he said, maybe √–121 is the same as √121 × √–1, which gives 11 × √–1.
Bombelli’s great breakthrough was to see that these strange, seemingly impossible numbers obey simple arithmetic rules once they are separated out from the other, more familiar types of number during a calculation. Everything after that was just grasping the nettle.
Proceeding with Cardano’s cubic equation, he eventually arrived at a solution:
x = (2 + √–1) + (2 – √–1)
Separate them out into what we would now call their real and imaginary parts, and it simplifies to 2 plus 2, and √–1 minus √–1. The imaginary part disappears, leaving us with just 2 + 2. So x = 4 is one of the solutions to x3 = 15x + 4. Plug it in and check for yourself.
These days, the convention is to use i to represent √–1. The Swiss mathematician Leonard Euler first came up with this. It’s easy to assume that i stands for imaginary, but the truth is, as with his e, Euler may just have picked it at random. Whatever the reason, Euler’s move has cemented i as the imaginary number in a very unhelpful way.
To see better what an imaginary number is, let’s think of a standard number line that runs from –1 to 1 (you can think of it as a ruler placed on a table in front of you, running from –1 on the left to +1 on the right). We call the process of moving along the line addition and subtraction (I’m at 0.3, and I’ll add 0.3 more, which takes me to 0.6). But we can also imagine making some moves by multiplication. If I start at 1, how do I get to –1? I multiply by –1. So let’s picture multiplication by –1 as half a rotation, anticlockwise, around a circle (in our case, the circle passes through 1 and –1). It’s actually a rotation by 180 degrees. In mathematicians’ preferred units to denote angles, 180 degrees is π radians (360°, a whole circle, is 2π radians).
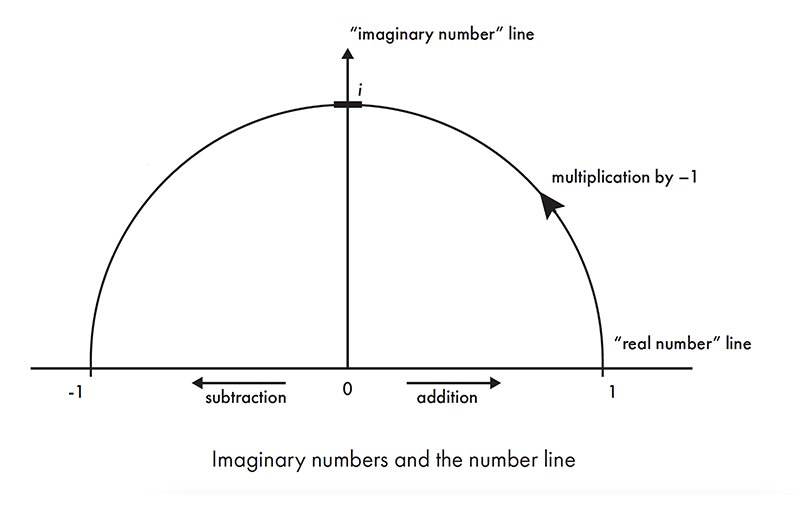
What happens if we only do half of this rotation? It’s halfway to multiplying by –1, which you can think of as the same as multiplying by √–1. That rotation, by just π/2 radians (or 90°) leaves our number up on the top part of the circle’s circumference, away from the standard number line. So we can think of the square root of –1 as sitting on a number line that runs at right angles to the number line we’re familiar with. It’s just another set of numbers, this time on a ruler that meets your other ruler at 90° to form a cross, with +1 at the end furthest from you, and –1 right in front of you.
That leads us somewhere interesting. The link with rotation in circles means that i is related to π and the sines and cosines of angles. That relationship is mediated through the strange number e, often called Euler’s number. This “irrational” number begins with the sequence 2.71828… and goes on forever. It is ubiquitous in mathematics and is vital to statistics, calculus, natural logarithms, and a range of arithmetic calculations. Euler worked out exactly what this looks like by taking a particular kind of infinite series (it’s called a Taylor series), and deriving something now known as Euler’s formula:
e±iθ = cosθ ± isinθ
This shows there is a fundamental relationship between the base of the natural logarithm and the imaginary number. What’s more, you can reduce this to the relation known as the Euler identity:
eiπ + 1 = 0
To some, this is a near-mystical formula. Here we have the base of natural logarithms e; the numbers 0 and 1, which are both unique cases on the whole number line; the imaginary number, a special case all of its own; and π, which as we know is a source of power in mathematics. Despite being discovered at different times by different people looking at different pieces of mathematics, it turns out they are interrelated, coexisting in this elegant, simple equation.
Seen from a slightly different perspective, perhaps we shouldn’t be surprised. As with π itself, there really isn’t anything mystical about this formula. It results from the fact that numbers change and transform themselves and each other through rotations. That only happens because of what numbers are: representations of the relationships between quantities. We don’t find anything mystical about moving along the familiar “real” number line by adding and subtracting. And there’s nothing different, really, about the transformations that come about through multiplications and divisions. Remember that sines and cosines are just ratios—one number divided by another—that are related to the angles within triangles, and you can represent those angles as fractions or multiples of π in units known as radians. So what we’re discovering here is not some deep mystery about the universe, but a clear and useful set of relationships that are a consequence of defining numbers in various different ways.
In fact, these relationships are more than useful—they could be described as vital. Take their application to science, for example: a full mathematical description of nature seems to require imaginary numbers to exist. The “real” numbers, of which we have learned so much, are not enough. They must be combined with the imaginary numbers to form the “complex” numbers that Bombelli first created. The result, says mathematician Roger Penrose, is a beautiful completeness. “Complex numbers, as much as reals, and perhaps even more, find a unity with nature that is truly remarkable,” he says in his book The Road to Reality. “It is as though Nature herself is as impressed by the scope and consistency of the complex-number system as we are ourselves, and has entrusted to these numbers the precise operations of her world at its minutest scales.” In other words, imaginary numbers had to be discovered because they are an essential part of the description of nature.
Michael Brooks is a United Kingdom-based science writer. His most recent book is The Art of More: How Mathematics Created Civilization.
Excerpted from The Art of More: How Mathematics Created Civilization by Michael Brooks. Copyright © 2022 by Michael Brooks. Excerpted by permission of Pantheon Books, a division of Penguin Random House LLC. All rights reserved. No part of this excerpt may be reproduced or reprinted without permission in writing from the publisher.
Lead image: agsandrew / Shutterstock