Our namesake, the nautilus, is not just a cultural and mythical object; it has also some rich (and not imagined) math to it. That’s because it is one of nature’s fractals. These are objects whose shape at a given length scale is mirrored by the shape of their smaller-scale parts. Fractals, in turn, extend well beyond mathematics, connecting physics to the stock market and contemporary music. And who better to tell us about this than Professor Benoit Mandelbrot, who discovered, named and defined the word “fractal”? Certainly one of the best-known mathematicians of the past 50 years, Mandelbrot grew up studying ellipses while hiding from the Nazis in the French countryside. After 35 years at IBM Research in upstate New York, and a professorship at Yale begun at the age of 75, his talks on the fractal became as well known as his shock of white frizzy hair. There was only one problem for us: Mandelbrot passed away in 2010. Undeterred, we tapped into 18 different sources, including three that were unpublished, to assemble a posthumous interview. The words in italics are ours; the rest are Mandelbrot’s. We missed our chance to have a conversation with the man; but we’re confident that if we had, it would have gone something like this. (A fully referenced version of the interview can be found here.)
You’re a mathematician interested in a lot of messy ideas. Why?
Circles, ellipses, and parabolas were my love when I was a young man, but are very rare in the wild. Galileo was absolutely right to assert that in science those shapes are necessary. But they have turned out not to be sufficient, merely because most of the world is of great roughness and infinite complexity. Take a broken stone. Everybody says it is complicated. I coined the word fractal from fractus, which is what the Latin refers to after the stone is broken. It’s rough and irregular, and broken up. Now, how do you describe the shape of a broken stone? How would you describe the shape of a broken piece of metal? Amazingly enough, the procedures used to define the roughness were very unsatisfactory and very much ad hoc, they did not at all catch the substance. Whereas with fractal geometry, the result is of extraordinary and pristine simplicity. It is the proper language to describe the nature of these shapes.
What is a fractal exactly?
There is no single mathematical definition of a fractal. To understand a fractal it is best to think of a tree. In a tree, if you take a branch, well, the branch with its sub-branches looks very much like the whole tree, but it is naturally smaller. If you take a smaller branch, again it is like the whole tree or like each branch. Therefore, a tree can be divided into parts and each part is very, very close to being identical to the whole tree. In the final analysis, fractal methods can serve to analyze any “system,” whether natural or artificial, that decomposes into “parts” articulated in a self-similar fashion.
So roughness and self-similarity are intimately linked. But is roughness really that important?
Roughness is ubiquitous in nature and culture—found in the distribution of galaxies and in the shapes of coastlines, mountains, clouds, trees, and the various ducts in the lungs; also in stock-price charts, paintings, music, and several mathematical constructions (well-known ones and those I fathered).
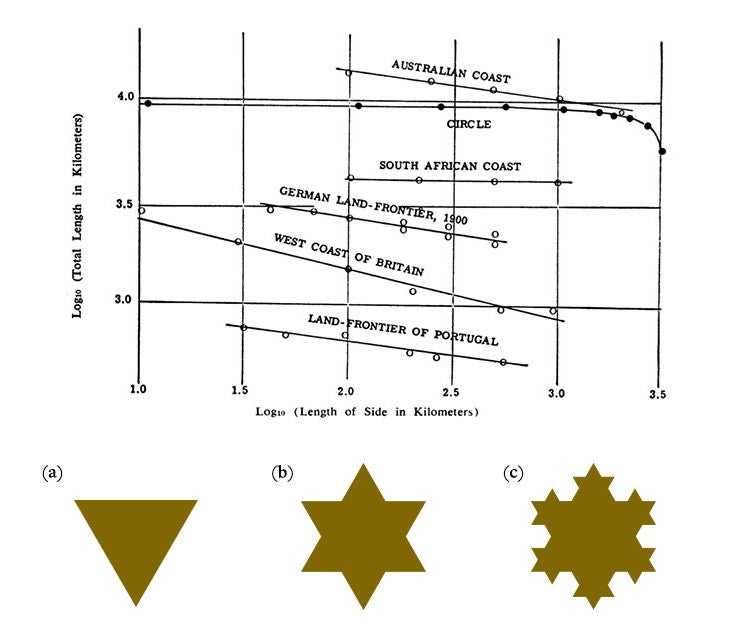
So you connected science to a lot of real-world situations.
I deeply wanted to identify some field where I could emulate Kepler—not Newton, not Copernicus, but Kepler. I put an extremely high value on the precise moment when an idea which is very abstract and removed from any applications—call it a toy—is made over into a tool and used to understand part of the messiness of nature. I always saw a close kinship between the needs of “pure” mathematics and a certain hero of Greek mythology, Antaeus. The son of Earth, he had to touch the ground every so often in order to reestablish contact with his Mother; otherwise his strength waned. To strangle him, Hercules simply held him off the ground.
Do you call yourself an applied scientist?
I call myself a mathematical scientist. It’s the official name of my chair at Yale and it was chosen with care. It is deliberately ambiguous. In a different era, I would have called myself a natural philosopher. Some people do call me an experimental philosopher, because this term has no other accepted meaning, and because there’s no question I’m a philosopher at heart. I am also a physicist, and an economist, and an artist of sorts.
You don’t sound like your typical academic.
One could describe almost any university as a collection of rather small and very narrowly based businesses: the various departments. My work was inspired by a strong belief that the division of science has been extremely harmful.
How so?
To an astonishing and dismaying degree, science has willingly lowered itself to a feature of professional sport, where an athlete’s worth is solely assessed within a narrowly defined event. To me, this makes the Olympics a very dull form of professional entertainment.
And you took pleasure from the opposite.
What has pleased me most is the fact that there are so many different aspects which under ordinary conditions should have been quite separate and without the organic links but which have developed entirely together at the same rhythm and in very different directions.
Did you pay a price for this approach?
Once, when still relatively young, I received from a top U.S. university, a very glamorous offer that was retracted the next day, after the dean became concerned by my professional activity in several other fields. Not knowing how to fit me in an existing peer-review pigeon-hole, that university saw no way to employ me. When working in economics, I was similarly dying to be allowed to make it known in my research papers that my methods were part of a general philosophy, of a certain approach to irregularity and chaos, and that they also mattered in physics. Invariably, the referees asked me to take these statements out. Later on, I went on to study turbulence and the editors forced me to cut out what they scorned as “dubious philosophy,” and to give more formulas and more details on the manipulations. In each case, I was pretending to be a technician in the field.
How did you develop an interest in economics?
The background resides in some work I had done earlier on an ancient topic—the law of distribution of personal income. I was invited to speak at a Harvard seminar directed by Hendrik S. Houthakker. Upon entering “Hank’s” office, I got a surprise that made that day one of the most memorable of my life. A peculiar diagram on his blackboard seemed to me nearly identical to one I was about to draw in my lecture! How was it, I soon asked, that something I had just discovered about personal incomes was already on display? “I have no idea what you are talking about. This diagram concerns cotton prices.” He had been working with a student before I arrived, and the blackboard had not yet been erased.
Why were the diagrams similar?
All price charts look alike. Sure, some go up, some down. But daily, monthly, annually, there is no big difference in their overall look. Strip off the dates and price markers and you cannot tell which is which. They are all equally wiggly. But that is exactly what we can now see in the cotton data: a fractal pattern. Here, the fractal scaling up and down is not being done to a shape, such as the florets of a cauliflower. Rather, it is being applied to a different sort of pattern, the way prices vary. The very heart of finance is fractal. So it all comes full circle. It was no coincidence that Houthakker’s cotton chart looked like my income chart. The math was the same.
You connected disparate ideas together visually.
It is the story of my scientific life: when I seek, I look, look, look, and play with pictures. One look at a picture is like one reading on a scientific instrument. One is never enough. A German-born friend of mine, a great biologist and philosopher, went so far as to theorize that progress in science consists in eliminating pictures as much as possible. Mathematics was perfect because it had completely banished pictures… even from elementary textbooks. I put the pictures back. This was received in a very hostile fashion by most of my colleagues. Since then, the opposition to pictures has weakened, simply because they have been so extraordinarily fruitful and because humans are continually changing.
Though this kind of a tool is not without its dangers?
Pictures can deceive as well as instruct. The brain highlights what it imagines as patterns; it disregards contradictory information. Human nature yearns to see order and hierarchy in the world. It will invent it where it cannot find it.
Why is this kind of thinking not more common?
Pictures are undervalued in science. They are not trusted. That is partly the 200-year-old legacy of the French mathematicians Lagrange and Laplace, who scrupulously labored to reduce all logical thought to precise formulae and carefully chosen words; sloppy diagrams were suspect. Their motivation was, I believe, partly technological: At that time drawings were imprecise and costly, a product of human hands. But in our lifetime the computer has changed all that.
Among the general public, you are best known for some of the beautiful fractal pictures that have come from your work.
Mathematics is an unreasonably effective source of beautiful shapes. They give us the privilege of competing with artists on their own terms. That is of creating shapes which may not be the equal of those by the greatest painters of creation, they are just beginners, they are not professional in that field. We are learning to draw. The Rembrandt or Picasso of computer art has not yet manifested himself or herself yet. But what we see already is very encouraging, that perhaps art by formula, may be the beginning of a new form of art.
Benoit’s Body Fractal Quiz
The human body is full of fractals. We’ve drawn some of them out. Can you guess which fractal shape goes with which body part?
Can art make math sexy?
Many of my friends commented that one of the great things about fractal geometry was that it improved their relations with their wives. For a long time they were telling their wives that what they were doing was so extraordinary beautiful, that they had found a fantastic beautiful theorem, fantastically beautiful proof of an old theorem, or a fantastically beautiful way of thinking about something. And their wives were sort of nodding saying “Yes dear.” Then the same husbands came back with pictures, for my things or their things, that used my kind of thinking and told their wives “You see, I have been telling you about the beauty …”
What makes fractal art so special?
Take even the most minimal artist’s art and try to describe it in a letter so precisely that the recipient is able to reproduce it exactly. To do so will require an extremely long description in words. But the equation that generates a fractal dragon is one line long, and if you give it to someone with the right intellectual and computing equipment he will be able to reproduce it exactly. So this art is the most minimal of all.
Is it unusual for math and art to interact in this way?
Mathematicians are different from all the other scientists and in fact all other humans, because mathematics trains you not to tolerate any ambiguity; it’s a requirement. But we deal with a new form of the controversial but ancient theme that all graphical representations of mathematical concepts are a form of art, one that is best when it is simplest, when, to borrow a painter’s term, it can be called “minimal art.” Is some of it reminiscent of M.C. Escher? It should be, because Escher had the merit of letting himself be inspired by the hyperbolic tilings in Fricke & Klein 1897. The fractal “new geometric art” shows surprising kinship to Grand Masters paintings or Beaux Arts architecture. It may well be that fractal art is readily accepted because it is not truly unfamiliar.
If the connection to art is so strong, artists themselves must have taken notice of your work.
A remarkably large number of artists had no vocabulary to express their grasp of the nature of fractals, yet such understanding comes through clearly in their work.
Can you give some examples?
There are several schools of strictly fractal music. [American composer Charles] Wuorinen uses fractal themes in his work very strongly, but he does not compose fractal music as such. [Hungarian composer] Gyorgy Ligeti is also an extremely good friend of mine. He said he had the feeling about a certain structure existing in music which no language could explain. He would sort of have to teach it to students more or less by example. And when he first saw the book on fractals he realized that this structure was simply fractal structure and he’s very much influenced by it. He confided to me that until he saw my pictures, he had not understood an important aspect of music: it is not free to do as it pleases, because it must be fractal. The schools of music never taught how to distinguish music from noise. Both Wuorinen and Ligeti came to me and said they understood at long last what music was like because they were taught in their young years that some pieces were too bare of detail, others would have too much detail and somehow, before music did anything else, it had to have proper patterns of small detail, medium-sized detail and big detail. If you listen to a Mozart sonata you see it very well; it’s cut into pieces and something changes all the time. And that elemental idea is essential to the acceptability of music.

And outside music?
The Russian painter Wassily Kandinsky was filmed as he worked on a sheet of paper about three feet square. He began with a slash across the whole and then added shorter slashes. When the film stopped, he was at work on many even shorter slashes, confirming a feeling I had looking at Kandinsky’s paintings: he understood fractality—perhaps not explicitly, but intuitively. Claude Lorrain, a French painter who worked mostly in Italy, painted landscapes that claim to be realistic, but in fact are extraordinarily simplified and easily interpreted in fractal terms. Joseph Turner’s extraordinary wild images of ships burning in the sea perfectly combine Euclidean and fractal shapes. Eugene Delacroix, in his “Advice to a Young Painter,” which can be found in the artist’s published letters, showed that he understood fractality intuitively, but at that time nobody could follow up. I feel very privileged to have filled the role of bringing together phenomena that scientists had missed, and painters or photographers have implemented but never formalised.
Why did fractals, in particular, resonate with artists?
In the 6th century before Christ, the idea of beauty was very much summarized: that before anything else, beauty means a balance between the part and the whole. Skilled artists must find arrangements, like mixtures of eddies of all sizes, that look balanced; does not that mean that elements of all sizes are distributed in a natural—that is, fractal—way? I never heard anyone say that the Paris Opera is not on a human scale, despite the fact that it’s an enormous building. Why doesn’t it elicit that feeling? Because the architect Charles Garnier made sure that his design would incorporate features of every scale.
What are some other examples of math resonating with art?
The first translation of Euclid was in the Florentine language; in other words, in Italian. Who were the first people in Italy who took account to Euclid? Not the mathematicians, but the architects and the painters. The painters, like Giotto around 1300, were looking for ways to represent perspective. They failed. Until, later on, Euclid became known and perspective became entrenched. In Pierre della Francesca’s works around 1500, perspective is so strong and so overwhelming, that for the first time I see that in a painting there is a separation of space and object. Many people believe that this influence of painting was very great on science; that science could then itself also separate the points of reference and the events happening in them.
So is there a two-way street between art and science?
I think it is wrong to separate art from science, and to split each activity into non-communicating pieces. I had a wonderful visit with [physicist Richard] Feynman not so long before his death, and we talked only about that: how can anybody claim to understand anything without having a picture or something and holding your hand? And he was very emphatic about the idea that anything that you have not expressed in these terms is incomplete and incomprehensible.
What about yourself? Did you see your work as art?
I mix mathematics and art every day. If the German language were not so reluctant to use kunst [art] freely, this opera-lover would describe his life effort as a Gesamtkunstwerk [all-embracing art form].
You identified strongly with the idea of a fractal, then.
Today you might say that, until fractal geometry became organized, my life followed a fractal orbit. I keep thinking of the wild ambition to survive and shine that has pushed me since adolescence. Each partial success aroused some old expectation or some old hunger. Ironically, this same pattern is one I have often dealt with in my research. Again and again, I have been blessed for a while with a competitive advantage over other scientists, but the reason is not at all that I am more powerful as a mathematician, but that my thinking had a way of proceeding along its own peculiar path. [The externals] of my life story appear continually broken. I had the feeling that I was pursuing some idea, some very, very dim thread through many fields, that because of my training and my willingness to be called a fool by going into fields in which I knew nothing—which I did all the time in my middle age—by going into fields where I had to spell my name again, and to be treated as a completely obnoxious outsider who just was perturbing the peace of the universe.
And what conclusion did this dim thread lead you to?
Mathematics, science and beauty are not separate activities of the mind. They are just the same. Different corners of one big and marvelous domain.
Any and all excerpts from the recently-published The Fractalist by Benoit B. Mandelbrot are excerpted by permission of Pantheon, a division of Random House, Inc. Copyright © 2012 by Benoit Mandelbrot. All rights reserved. No part of this excerpt may be reproduced or reprinted without permission in writing from the publisher. The book can be purchased here.
Click here for a list of references.


























