Space is brutally egalitarian. When you become separated from your lover, the two of you retain no tighter a physical connection than do two lumps of coal. In this way, space serves as the organizing principle of the natural world—the glue that binds the universe together, as the English physicist Julian Barbour has put it. Physical objects do not interact willy-nilly; their behavior is dictated by how they are related to one another, which depends on where they lie in space at a given time. This structuring role is easiest to see in the classical laws of mechanical motion, but also occurs in field theories. The value and rate of change of a field at different points in space fully determine what the field does, and points in the field interact only with their immediate neighbors.
This kind of behavior reflects what scientists call “locality,” which means that everything has a place. You can always point to an object and say, “Here it is.” The world we experience possesses all the qualities of locality. We have a strong sense of place and of the relations among places. Locality grounds our sense of self, our confidence that our thoughts and feelings are our own. With all due respect to John Donne, every man is an island, entire of himself. We are insulated from one another by seas of space, and we should be grateful for it.
But locality isn’t what it used to be. Quantum mechanics predicts that two particles can become blood brothers. For want of a mechanism to couple them, the particle should be completely autonomous—yet to touch one is to touch the other, as if distance meant nothing to them. The scientific method of divide and conquer fails for them. The particles have joint properties that escape you if you view them one at a time; you must measure the particles together.

Our world is crisscrossed by a web of these seemingly mystical relationships. And in the past 20 years, I’ve witnessed a remarkable evolution in attitudes among physicists toward locality. In my career as a science writer and editor, I have had the privilege of talking to scientists from a wide range of communities—people who study everything from subatomic particles to black holes to the grand structure of the cosmos. Over and over, I heard some variant of: “Well, it’s weird, and I wouldn’t have believed it if I hadn’t seen if for myself, but it looks like the world has just got to be nonlocal.”
To make sense of nonlocality, the first step is to invert our usual understanding of space. Physicists and philosophers can define space as the fact that the natural world has a very specific structure to it. Instead of saying that space brings order to the world, you can say that the world is ordered and space is a convenient notion for describing that order. We perceive that things affect one another in a certain way and, from that, we assign them locations in space. This structure has two important aspects. First, the influences that act on us are hierarchical. Some things affect us more than other things do, and from this variation we infer their distance. A weak effect means far apart; a strong effect implies proximity. The philosopher David Albert calls this definition of distance “interactive distance.” “What it means that the lion is close to me is that it might hurt me,” he says. This is the opposite of our usual mode of thinking. Rather than cry, “Watch out, the lion is close, it might pounce!” we exclaim, “Uh-oh, the lion might pounce on me; I guess it must be close.”
That’s what space is. It’s data compression on a massive scale.
The second aspect of the spatial structure is that diverse influences are mutually consistent. If a rhinoceros is also able to hurt me, it must be close, too. And if both a lion and a rhino are able to hurt me, then the lion and rhino should also be able to hurt each other. (Indeed, my survival depends on it.) From this patterning of influences, we extract space. If the threat posed by predators couldn’t be expressed in terms of spatial distance, space would cease to be meaningful. A less morbid example is triangulation. The signal bars on your mobile phone indicate the strength of the phone’s connection to a cell tower and therefore your distance from that tower. In an emergency, the phone company can locate your phone by measuring your signal at several towers and using triangulation or the related technique of trilateration. The fact that the measurements converge on a single location is what it means for you to have a location.
The nice thing about defining space in terms of structure is that it sidesteps some of the long-running disputes over the nature of space. The ancient atomists (as well as Isaac Newton) conceived of space as a thing in its own right, whereas Aristotle (as well as Gottfried Leibniz and Ernst Mach) conceived it an abstraction that describes how the contents of the universe are packed together. Either way, though, space reflects a structure that the natural world possesses. If the atomists were right and space has an independent existence, it must be highly ordered, like a neatly woven fabric, so that it can serve the functions that physics demands of it. If space is merely an abstraction, then the contents of the universe must fit together in just the right way to give meaning to the abstraction.
On the face of it, we haven’t gained anything by giving primacy to organization; we’ve merely traded one mystery for another, because now we’ve got to explain the organization. But this could be an opportunity, because now we can imagine what the universe would be like if it weren’t ordered in the requisite way. Then it might not be spatial anymore. Instead of thinking of space as an absolute necessity, we can regard it as one of the possible states of the universe, just as ice is one of the possible states of water. The ice analogy isn’t bad, actually. Water is solid over a narrower range of conditions than it is gaseous. Likewise, space may be the exception, not the rule; most proposed unified theories of physics suggest that the vast majority of the universe’s possible states are nonspatial. “Where space-time exists is very nongeneric,” says Moshe Rozali, a string theorist at the University of British Columbia. “It requires some special conditions.” In the twilight between order and disorder, space and spacelessness, perhaps we can find a comprehensible explanation for the nonlocal phenomena that physicists have puzzled over.
You don’t need a complex system of moving, interacting parts to appreciate the organizing power of space. Consider the geography of a country. You can think of the cities as laid out on a map or you can express their mutual spatial relations with a mileage chart, like those found in paper road maps and atlases—one of those rectangular or triangular grids giving the distances between pairs of cities. What’s interesting is that the chart contains hidden patterns within it, just as jigsaw puzzle pieces look unrelated when you dump them out of the box but show their affinity as you fit them together.
Suppose you have 20 cities. The chart contains 400 numbers. To fill in the data, a map company such as AAA hires drivers to travel from city to city and jot down the odometer mileage or take GPS readings. In terms of real information content, the chart is highly redundant. The distances obey very specific rules that mathematicians call “distance axioms.” To begin with, the 20 numbers running along the diagonal are zero—the distance from each city to itself. Of the remaining numbers, half are repeats, since distances are symmetrical: A car driving from Dallas to Salt Lake City covers basically the same ground as a car going the other way. Indeed, most map companies leave off this redundant information and show only the remaining triangle of numbers.
Even the 190 quantities in that triangle are not fully independent of one another, because you can boil them down to 60 values representing each city’s coordinates—latitude, longitude, and altitude—as well as an additional value for Earth’s radius when cities are far enough apart that the planet’s curvature becomes a factor. Finally, you can lose several more numbers because the conventions used for the coordinate system (such as taking the prime meridian to be zero degrees longitude) don’t matter for the purposes of driving distances. That knocks out another six quantities. So now you’re down to 55. The 400 numbers you started with are just various arithmetic combinations of 55 numbers. That may not be obvious from looking at the chart, but you know it has to be true because you could reverse the process. You could start with the cities’ coordinates, mark their locations on a map, and use trigonometry to calculate the intercity distances.
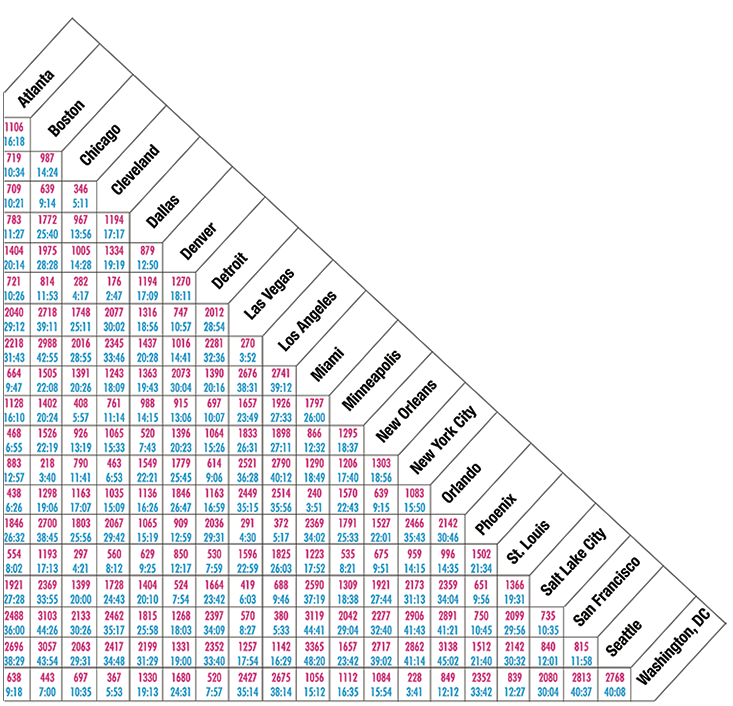
So the chart is highly ordered. This is what it means for the cities to be situated within space. Spatial coordinates are a highly economical way of capturing the possible mutual relations among things. In the above example, we had 20 cities and 400 intercity distances that reduce to 55 unique numbers. The more things you have, the more impressive the savings are. For 100 cities, the chart contains 10,000 intercity distances, reducing to 295 numbers. For all the world’s cities, or all its towns, or all its geographical features of any type, the raw distance data would consume a hard drive even though the positions of those features can be concisely expressed on a single map. “That’s what space is,” Barbour says. “It’s data compression on a massive scale.”
The reason the compression is so powerful is locality. Locality means that the whole is the sum of its spatial parts, and in this context, that means every journey is a series of smaller steps. You can build up long distances from shorter intermediate ones, so you don’t need to specify each and every pair of directions. For instance, the chart might tell you it’s 900 miles from Dallas to Denver and 500 miles from Denver to Salt Lake City, so you don’t need to be told it’s at most 1,400 miles from Dallas to Salt Lake.
Suppose this weren’t the case—suppose the data in the chart weren’t so highly ordered. If I fill in a chart with 400 random numbers and ask you to mark their locations on a map, you’ll almost certainly fail. For instance, the chart might tell you it’s 900 miles from Dallas to Denver, 500 miles from Denver to Salt Lake City, and 8,000 miles from Dallas to Salt Lake. Now, that doesn’t make much sense, does it? These data put Salt Lake City in two different places, depending on whether you drive straight from Dallas or stop off in Denver. The situation is like an April Fool’s joke in which your friend mixes together pieces from different jigsaw puzzles and gives them to you to assemble. You’ll struggle to fit the pieces together until it dawns on you that your supposed friend is a cruel prankster.
Under such circumstances, position becomes meaningless. Space becomes meaningless. It’s not a useful way to describe the relations among places anymore. But that doesn’t mean the relative arrangement of cities is incomprehensible. Even if you can’t place the cities on a map, you can fall back on the full mileage chart. In other words, you can use what philosophers call the “unmediated” distances, the ones that directly link pairs of cities and can’t be reduced to a series of shorter hops. This isn’t an entirely hypothetical situation. When I first drove in Boston, I had to learn to distrust my spatial awareness, because it kept getting me lost. In that maze of one-way streets and amoeba-shaped “squares,” you routinely have to go west to go east, or get in the left lane to turn right. It does you no good to know where places are located from a bird’s-eye view; instead, you need to robotically follow directions for where and how to turn. To a driver, Boston is a nonspatial city.
It’s really not so strange that networks of relations can burst out of space. This is the case, after all, for human relationships. Our social lives are too tangled to be laid out on a spatial map. Not that people don’t try. Family trees translate genetic and conjugal closeness into spatial closeness, and online social networks have spawned similar attempts. The Wolfram Alpha website, for example, used to be able to map out your Facebook friends network, using dots to symbolize your friends and lines to connect those who have friended each other.1 Spatial distance on the map represents social proximity as judged by the number of friends people have in common. Typically, your friends cluster into distinct social circles: family, classmates, workmates, ultimate Frisbee teammates, fellow Radiohead groupies, and so on. If these people go to the same party, they might congregate in different corners of the room, and the figurative distance between them translates into literal distance.
When I first generated a Facebook graph, I noticed a stray link between my physics colleagues and my music friends, revealing that a theorist I’d worked with shared my passion for Cuban dance music. Finding unexpected connections is half the fun of these graphs, but does expose the limitations of the spatial metaphor. There’s no consistent way to assign that theorist a location on my graph. Like Salt Lake City in the above example, he occupies two different places, corresponding to two social circles. And the failure deepens when you consider everything these graphs leave off. Two Facebook “friends” may have never met or spoken, yet the diagram links them as if they were BFFs. One person might have an unrequited crush on the other, and still a line connects them. To capture these other dimensions of human relationships, you can festoon family trees with symbols: thick line for a close bond, zigzags for hostility, and so on. Such diagrams, known as genograms, are popular among psychologists, social workers, and people struggling to follow Game of Thrones. The symbols compensate for the failure of the spatial metaphor.
Spacelessness and space are just two different phases of the same network of grains.
In some cases, people organize themselves so that their social network becomes radically streamlined, and these situations let us see how space might emerge from spacelessness. A structure can form where none existed before. That can happen in two ways: Build up or cut back. People might start as atomized individuals who begin interacting, like your grandmother who finally got on Facebook and signs up all her friends. Or they might start with a mess of existing relations and prune them, like a social butterfly who friended everyone he met, realizes he doesn’t know who half of them are, and does a friends purge.
The army, for example, restricts socializing across ranks, on the assumption that familiarity might breed contempt. Consequently, difference in rank is analogous to spatial separation: A private is distant from a colonel in much the same way that Dallas is distant from Salt Lake City. Information flows up and down the chain of command just as a person driving from Dallas to Salt Lake City must pass through intermediate points. Because of this structure, a military hierarchical chart is a fair representation of social relations in the military.
The army’s structure is imposed by military discipline, but in other cases the order develops spontaneously from within. A classic example is the market economy. We routinely speak of “the economy” as though it were a conscious being rather than millions of people making rash decisions with their money. And in a sense it is, because collective arrangements transcend the people who create them. In isolation, individuals don’t put price tags on goods, because they have no one to buy from or sell to. Price becomes important when people come together and trade. Depending on their haggling skills, the price varies from person to person and place to place. Some plucky entrepreneur takes advantage of these variations to buy low and sell high; in so doing, that person helps to even out the supply and therefore harmonize the prices.

This kind of self-organizing happens all the time in physics. For instance, a single water molecule has no temperature. Temperature becomes meaningful when molecules collide and exchange energy. If you mix cold and hot water, the cold warms up, the hot cools off, until they equalize. Before equilibrium, the water is characterized by two temperatures; afterward, by a single value. From complexity comes simplicity. The complexity remains latent, though. You can tell it’s there whenever the temperature fluctuates or water undergoes a transformation such as boiling in a teakettle. Physicists commonly use these deviations from standard behavior as windows into the microscopic composition of materials.
The same might go for space, too. The basic building blocks of nature might be capable of a tangle of relationships that would fill a celebrity gossip rag. Through some organizing mechanism or simply the play of averages, those relationships become regimented, so that they can be laid out on a spatial grid and interact only in strictly prescribed ways. A mind-bogglingly complex network of interactions reduces to a few numbers that we call “the position” and “the time.” The underlying complexity never goes away, though. In situations such as black holes, the system can become disordered and events can cease to have a position or a time. And even when the system is spatial, it contains a vast amount of latent complexity. The universe we see playing out in space may be just the surface level, where we float like little boats while leviathans stir in the deep.
The concept of space as a network goes back to the 1960s and the brainstorms of such innovative (and iconoclastic) theorists as John Wheeler, David Bohm, Roger Penrose, and David Finkelstein. Wheeler, for one, imagined taking a bucket of “dust” or “rings”—primitive grains of matter that do not exist within space, but simply exist—and stringing them together to form space. Physicists have been trying to make the idea work for decades. Today one of its strongest champions is Fotini Markopoulou, who pictures the stringing-together process as a graph akin to those Facebook diagrams. She and her colleagues call their approach “quantum graphity”—cutesy, but any effort to inject a sense of humor into physics jargon has got to be a good thing.
Quantum graphity doesn’t specify what the Wheelerian grains actually are—that’s a job for a full-up theory of quantum gravity such as loop quantum gravity or string theory. Quantum graphity is a theory-in-miniature that focuses narrowly on what you might build with those grains. Indeed, Markopoulou and her colleagues’ philosophy is that the detailed composition shouldn’t matter; the principles of organization should be universal. After all, physicists have found that similar rules govern a huge diversity of complex systems, from earthquakes to ecosystems to economies. On the downside, quantum graphity is so bare-bones that it faces the problem of meshing with known physics. “Fotini tries to jump straight in, but it’s very ambitious and dangerous, because you have no connection to existing theories,” says Claus Kiefer of the University of Cologne.
This thing has no notion of locality … If you just put out your hand, you reach everybody in the whole universe.
The links between the elementary grains are as simple as can be. Two grains are either connected to each other or not, like Facebook users who can either be friends or not—just an on-or-off relationship. The resulting network looks like a string-art craft project in which you hammer nails (representing the grains) into a sheet of wood and stretch threads (the links) among some of them. Despite the simplicity of its construction, the network can take on a huge variety of shapes, ranging from skeletal outlines to elaborate mandalas.
To breathe life into the network—to give it the capacity to transform and evolve—Markopoulou and her colleagues suppose that the links switch on or off depending on the amount of available energy. This process is ad hoc, but again the goal is not to create a bulletproof theory, but to reconnoiter possibilities for how to construct space. Each link represents a certain amount of energy. Chains of links contain less energy than an equivalent number of isolated links, so the total energy of a network depends not only on the sheer number of links, but also on how they’re put together. The more intricate the pattern is, the more energy it embodies.
The energy maxes out in a fully interconnected network, where every grain is linked to every other grain. In such a network, the principle of locality doesn’t hold; you can go from any grain to any other grain in one hop, without passing through any intermediate points. The network lacks the hierarchy of relations—near versus far, small versus big—which is characteristic of space. You can’t subdivide it into separate chunks; it’s an indivisible whole. “This thing has no notion of locality … ,” Markopoulou has explained. “If you just put out your hand, you reach everybody in the whole universe.”
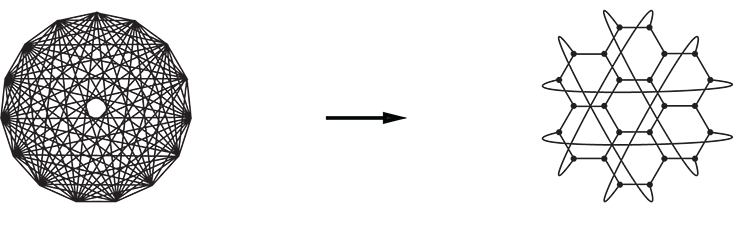
To see why the high-energy network is not spatial, try assigning locations to the grains. Every grain has to be equidistant (a single hop) from every other. For the first three grains, that’s no problem: Arrange them in an equilateral triangle. Four can be stacked in a pyramid. But where does a fifth go? There’s nowhere equidistant to the first four points, at least not within ordinary, three-dimensional space. You need a four-dimensional pyramid. In fact, each additional grain requires a whole new dimension of space. Before long, you enter an ultra-higher-dimensional realm beyond our capacity to visualize. And most of that vast venue is wasted: The network is only one hop wide in any direction and does a good impression of a balled-up spider’s web. So although you might still talk of the network as existing within space, it’s not the kind of space we want: three dimensions that extend as far as we can see in every direction and provide an economical description of the relations among objects.
Lower-energy patterns are a different story. They’re just what we want. Each grain connects to just a few others, forming a regular grid like a honeycomb or woven fabric. The notion of distance regains meaning: Some grains are close together, the rest far apart. The network is nice and roomy. The principle of locality holds: For an influence to go from one place to another, it can’t hop straight there, but must work its way through the network. The passage of the signal takes time, which would explain why the speed of objects through space is limited (by the speed of light).
In short, spacelessness and space are just two different phases of the same network of grains. One can metamorphose into the other; a crumpled wad can unfurl into a flat expanse. Theorists have proposed a couple of ways this might happen. The reshaping could be a process that occurs in time. The network starts off as sizzlingly hot—a highly interconnected pattern containing an enormous amount of energy. Then it cools off and crystallizes like a tray of water freezing to ice, as links dissolve and reorganize to create a tidy arrangement. The trick is to explain the cooling. Things don’t just cool down on their own; something must drain them of heat. “Where did the energy go?” wonders Markopoulou. “You need a freezer. You need to cool the universe.” She and her colleagues speculate that the energy could go into the creation of matter. The primordial grains could coalesce into elementary particles, so that matter emerges hand in hand with space.
Alternatively, the transition may not be a process that unfolds in time, but a structuring that arises at the quantum level. The network can exist in multiple conditions at once, a limbo known as superposition. Although most of those conditions are nonspatial, they can fuse together into something that is spatial. The best-developed account of superposition of space goes by the somewhat unwieldy name of “causal dynamical triangulations.” Its inventors have shown that nonspatial geometries neutralize one another, as long as events are highly ordered, with a distinction between cause and effect built in from the outset. The effect is analogous to the wisdom of crowds, those remarkable cases in which you pose a question to a group and no one person has the right answer, yet pooling everyone’s guesses does give the right answer. The classic example is the jelly-bean experiment: If you ask a group of people how many jelly beans there are in a jar, the average of their estimates will be better than any single person’s estimate. The group has a collective intelligence beyond that of its members.
String theorists have explored ideas similar to Markopoulou’s quantum graphity. In the 1990s they pioneered “matrix models,” so called because the equations are based on grids, or matrices, of numbers much like the mileage charts. A matrix in the mathematical sense has nothing to do with the virtual-reality “matrix” of the movie The Matrix, yet the premise is eerily similar: The world we experience is a kind of simulation generated by a deeper level of reality. The best-known matrix model was developed by a quartet of theorists, Tom Banks, Willy Fischler, Steve Shenker, and Leonard Susskind. Their model, like quantum graphity, supposes that the universe is a cat’s cradle of interconnections among grains of primitive matter. Under the right conditions, extraneous connections rupture and the grains snap into a regular spatial grid. “You start with a bunch of Tinkertoy parts with no particular structure to them,” says Susskind, who is a physics professor at Stanford University. “You shake it up and it emerges into a lattice or structure of some sort.”
String theory outgrew its name long ago. It postulates not just one-dimensional strings, but also two-dimensional membranes and higher-dimensional analogues—as theorists call them, 1-branes, 2-branes, 3-branes, 4-branes, and so on. Some branes, designated by D, can act as the endpoints of strings. At the bottom of this pecking order is the humble D0-brane, a type of particle. Being a true geometric point lacking size or any other spatial attribute, the D0-brane is the perfect building block for space. Confirming this intuition, theorists calculate that the D0-brane has the right properties to serve as the graviton, the particle that has been hypothesized for decades to convey the force of gravity.
Matrix models take this particle as fundamental and construct the universe entirely from lots of them. Every particle can interact with every particle, and their interactions are not simply on or off, but can vary in strength and in quality. The more energy you inject into a pair of particles, the tighter their bond will become. The namesake matrix of numbers quantifies this web of interactions. For example, if you read down to the eighth row and then across to the 12th column, the number there will tell you how strongly particle number eight interacts with particle number 12. To express not just the raw strength but also the quality of the connection, you need several such matrices.
We have only a vague awareness of riding on a giant ball of rock, and bacteria know nothing of our daily struggles. Nature is stratified by scale.
Each matrix is a square, and running diagonally from the top left corner to the bottom right is a special set of numbers—where the eighth row meets the eighth column, the 12th row meets the 12th column, and so on. These tell you how much each particle interacts with itself. Self-interactions are a core feature of matrix models. The particles are subatomic narcissists, the physics equivalent of Facebook users who always “Like” their own posts. Their self-interactions have a carefree, unrestrained quality; you can dial their strength up or down without having to pump in energy.
Whereas the workings of quantum graphity are somewhat ad hoc, the laws governing D0-branes are dictated by considerations of symmetry. The mathematical balance of the equations is the organizing principle of this model. Symmetry ensures that the off-diagonal values in the matrix are yoked to the diagonal values—in other words, that the branes’ mutual interactions depend on their self-interactions. Particles that self-interact by comparable amounts forge a bond, whereas particles with differing levels of self-interaction remain aloof. Put simply, like attracts like. Consequently, the branes agglomerate into separate clusters like the social circles in your Facebook network. These clusters constitute the ordinary subatomic particles of physics. Each cluster can be compactly described by a few numbers—namely, the strength and quality of its constituents’ self-interactions.
That’s how space arises in matrix models. The D0-branes don’t live or move within space. Mathematically they all sit on top of one another at a single point. But because they’re so selective about their interactions, they produce our experience of living within space. What we call “position” is simply the set of numbers that uniquely identifies a given cluster. It’s like pigeonholing your friends as “physics lovers,” “Radiohead groupies,” or “Cuban-style dancers.”
That’s just the start. You can take all our familiar spatial notions—movement, size, locality—and explain them in terms of brane dynamics. Movement: Things shift their position because the D0-branes’ self-interactions are varying. It’s like saying the Cuban dancers suddenly all get interested in Dominican music. They “move” as a group to a new passion. Such movement may sound metaphorical, but in matrix models it’s the origin of physical movement. Size: The self-interactions of the branes in an object are not exactly equal, but have a slight spread, so that the object spans a range of positions. Locality: Clusters at separate locations are independent because their self-interactions differ, which suppresses their mutual interactions according to the logic of symmetry. This is like saying that Cuban dancers and Radiohead groupies never have much to say to each other. “Things that are ‘separated’ are not really separated,” Susskind explains. “There’s just a cancellation of the things that are connecting them.”
If all the branes did was reproduce space, that’d be gratifying, but boring. Our goal is to go beyond space. Branes can do that. They can behave in ways that are too complicated to represent with a handful of spatial coordinates. For instance, the mutual interactions among clusters are never fully suppressed, because quantum effects keep tickling them back to life. Therefore, spatially separated clusters are not fully independent; they feel the gentle tug of other clusters. This is how matrix models explain the force of gravity. In a sense, the models evoke Newton’s picture of gravity as a nonlocal force that leaps from one thing to another. The interactions that produce it aren’t transmitted through space, but are direct, unmediated, nonlocal links.
Another departure from spatiality occurs inside clusters. The internal group dynamics are intense and every brane is interacting with every other. The branes scramble one another’s self-interactions, and the matrix values representing those interactions lose the qualities of spatial coordinates. Ordinarily, coordinates are independent numbers: You can measure the latitude of a city separately from its longitude. But you can’t do that for branes within a cluster. If you measure the latitude of a brane first, then its longitude, you might get a different result than if you measured the longitude, then the latitude. This kind of ordering effect is known mathematically as “noncommutativity.” In effect, the particle seems to be located in two different places, like Salt Lake City in my cities example. “The position in, say, the ‘x’ direction and the position in the ‘y’ direction can’t simultaneously be measured,” says Emil Martinec, a string theorist at the University of Chicago. “This is certainly not the behavior we expect for a collection of discrete particles—we expect to be able to localize them precisely in all spatial dimensions.” The degree of ambiguity is a measure of just how nonlocal and non-spatial the system is.
Indeed, the cluster doesn’t really have an “inside”— there is no volume of space where the D0-branes bustle around. Arguably there aren’t even any D0-branes anymore, either, because they surrender their individuality and become assimilated into the collective. If you look at a cluster from the outside, what you see isn’t the outer surface of a material thing, but the end of space; and if you poke your hand into the cluster, you will not reach into its interior, for the cluster has no interior. Instead, your hand will become assimilated, too (which can’t be good for it). If you wisely refrain from touching the cluster and instead throw particles into it, you will notice that the cluster’s storage capacity depends on its area rather than on its interior volume—again, for the simple reason that it doesn’t actually have an interior volume. Space has no meaning at this level.

Matrix models do have some peculiarities, but they establish a remarkable principle: A bunch of particles obeying quantum physics can organize themselves so that you’d swear they live and move within space, even if space wasn’t in the original specification of the system. And it turns out that this principle is very general. Not just a swarm of D0-branes but almost any quantum system contains spatial dimensions folded inside it like a figure in a pop-up book. Most such systems don’t bootstrap space from utter spacelessness, as matrix models do, but prime the pump with a low-dimensional space in order to generate a higher-dimensional one.
The AdS/CFT duality is such a system. It starts with a three-dimensional space and generates a nine-dimensional one. One reason string theorists like this scenario so much is that it neatly explains the holographic principle, the idea that the universe can sustain much less complexity than the principle of locality would lead you to expect. The complexity is reduced by just the amount you’d expect if one of the dimensions of space were illusory. In the AdS/CFT scenario, that’s because the dimension in question is illusory. It can be collapsed down like an accordion because it was never really there. (“Illusory” is perhaps the wrong word. “Derived” or “constructed” would be better, if less poetic. The dimension may not exist at the lowest level, but it is still very real to anything larger than a brane.)
The disposable dimension reflects a particular aspect of order in the underlying quantum system. In fact, the requisite order is familiar to us from everyday life—specifically, the fact that big things and small things live as if in worlds apart. Our planet trundles around its orbit oblivious to human affairs, just as we spare little thought for the bacteria that lodge in our skin. Conversely, we have only a vague awareness of riding on a giant ball of rock, and bacteria know nothing of our daily struggles. Nature is stratified by scale.
Sound waves are an especially simple example of this stratification. Sounds of long and short wavelengths are oblivious to each other; if you sound a deep bass note and a high treble pitch simultaneously, each ripples through the room as though it were the only sound in the world. Their mutual independence is analogous to the autonomy of spatially separated objects. Suppose you play two piano keys, middle C and the adjoining D key. The C key creates a sound wave with a wavelength of 1 meter 32 centimeters, and D produces one with a wavelength 14 centimeters shorter. These waves overlap in the three dimensions of space through which they propagate, yet they’re independent of each other, as if they were located in different places. In a sense, you can think of the sound waves as residing 14 centimeters apart within a fourth spatial dimension.
The farther apart the keys are on a piano keyboard, the farther apart they are within this imaginary dimension; a given distance along the keyboard translates into a given distance within the dimension. You don’t see this dimension as such; to you, it’s an abstraction that captures the acoustical independence of sound waves. But it’s a remarkably fitting abstraction. Musicians call the difference between pitches a musical “interval,” which has connotations of distance, as if our brains really do think of the differences between pitches as spatial separation. AdS/CFT duality takes this abstraction literally and suggests that one of the dimensions of the space we occupy represents the energy or, equivalently, the size of waves within the underlying system.
Physics does need to have some foundational structure, something that everything else is built on, and time is as good a candidate as any.
Raman Sundrum, a particle theorist at the University of Maryland, has a dramatic way of putting it. (In fact, it’s so dramatic that you’d be tempted to dismiss it as fanciful if it weren’t backed up by rigorous mathematics.) Suppose you’re an artist painting the National Mall, with an ice-cream stand in the foreground and the Washington Monument in the background. To evoke a sense of distance on the flat canvas, you draw these two objects at different scales. Something like that is happening for real in the AdS/CFT scenario. The universe looks three-dimensional, but could really be a two-dimensional canvas, and what we perceive as distance along the third dimension is ultimately a difference in scale. “The depth dimension could be recreated in the way that artists have to do it: by just drawing the Washington Monument really small and drawing something in the foreground really big,” Sundrum says. A faraway object is actually sitting right next to you; it looks small because it really is small. You can’t touch it not because it’s distant but because it’s so tiny that your fingers lack the finesse to manipulate it. When things grow or shrink, we perceive that as movement toward or away from us.
Things of different sizes aren’t strictly independent; they interact with things of comparable size, and the effects can cascade from one scale to the next. Consider the proverb of the nail: For want of a nail, the shoe was lost; for want of a shoe, the horse was lost; then the knight, the battle, and the kingdom. A nail shortage in a single blacksmith shop didn’t immediately cause the monarch’s downfall; it exerted its influence indirectly, via systems of intermediate scales. Sound waves of different pitches can also behave like this. A Chinese gong begins rumbling at a low pitch and gradually vibrates at successively higher pitches. The necessity of propagating through scale explains why spatial locality holds in the emergent dimension. What happens in one place doesn’t jump to another without passing through the points in between.
It’s not automatic that the underlying quantum system would possess this kind of hierarchical order. Just as a painting must be composed in just the right way to produce the sense of depth, so must the system have a certain degree of internal coherence to give rise to space. What ensures this cohesion is entanglement among the system’s particles or fields. To produce space as we know it, those particles or fields must be entangled by scale: each particle with its neighbor, each pair of particles with another pair, each group with another group. Other patterns lead to different geometries or systems that can’t be thought of as spatial at all. If the system is less than fully entangled, then the emergent space is disjointed, and an inhabitant of the universe would be trapped inside one region, unable to venture elsewhere. “Quantum entanglement is the thing that is responsible for connecting up the spacetime into one piece,” says Mark Van Raamsdonk, a theorist at the University of British Columbia. When we first encountered entanglement, it seemed to transcend space. Today, physicists think it might be what creates space.
It’s astounding to think that space, thought for so long to be the rock-bottom foundation of physical reality, could perch atop an even deeper layer. Ironically, the main criticism I hear of quantum graphity, matrix models, and AdS/CFT isn’t that they’re too weird, but that they’re not weird enough. All these models still work within the basic framework of quantum physics and general relativity, and much of the structure that is supposed to arise spontaneously is actually preprogrammed into the rules.
Notably, these models presuppose time; they don’t incorporate Leibniz’s and Mach’s suggestion that time should emerge as surely as space does. Some researchers don’t see this as a failing, but as a profound truth about nature—that time must be fundamental even if space isn’t. After all, physics does need to have some foundational structure, something that everything else is built on, and time is as good a candidate as any. Indeed, how could you even talk about emergence as a temporal process if you don’t presume time? “As soon as you say time is emergent, you run off the rails,” Martinec says. “What are the rules? What do I do?” The Caltech physicist Sean Carroll has put it succinctly: “Space is totally overrated, whereas time is underappreciated … I think that time is going to last … Space, on the other hand—totally bogus. Space is just an approximation that we find useful in certain circumstances.”
Yet this separation of time and space runs counter to Einstein’s great insight that the two are fundamentally inseparable. If one is emergent, surely the other must be. Many physicists do think that time emerges and have been looking for ways to think of emergence without presupposing time. The key is the existence of a boundary. If the universe has a boundary located out in deep space, the emergent dimension is spatial, but if it has a boundary in the past or future, the emergent dimension is temporal. In fact, as far as astronomers can tell, our universe has temporal rather than spatial boundaries. In the past, there’s the big bang; in the future, eternally accelerating expansion, which also serves as a type of boundary. An observer sitting on that boundary in the distant past or far future would know all there is to know about the intervening moments. Yesterday, today, and tomorrow would collapse into one.
By this logic, theories that presume time are still incomplete, merely stepping stones to a complete account of how space and time emerge from deeper physics. Theorists will need an even more radical approach.
George Musser is a writer on physics and cosmology and the author of The Complete Idiot’s Guide to String Theory and Spooky Action at a Distance. He was a senior editor at Scientific American for 14 years and has won the American Institute of Physics Science Writing Award, among others.
Excerpted from Spooky Action at a Distance: The Phenomenon That Reimagines Space and Time—and What It Means for Black Holes, the Big Bang, and Theories of Everything, by George Musser, published by Scientific American/Farrar, Straus and Giroux, LLC. Copyright © 2015 by George Musser. All rights reserved.























