Nine years ago, I was sitting in a college math physics course and my professor spelt out an idea that kind of blew my mind. I think it isn’t a stretch to say that this is one of the most widely applicable mathematical discoveries, with applications ranging from optics to quantum physics, radio astronomy, MP3 and JPEG compression, X-ray crystallography, voice recognition, and PET or MRI scans. This mathematical tool—named the Fourier transform, after 18th-century French physicist and mathematician Joseph Fourier—was even used by James Watson and Francis Crick to decode the double helix structure of DNA from the X-ray patterns produced by Rosalind Franklin. (Crick was an expert in Fourier transforms, and joked about writing a paper called, “Fourier Transforms for birdwatchers,” to explain the math to Watson, an avid birder.)
You probably use a descendant of Fourier’s idea every day, whether you’re playing an MP3, viewing an image on the web, asking Siri a question, or tuning in to a radio station. (Fourier, by the way, was no slacker. In addition to his work in theoretical physics and math, he was also the first to discover the greenhouse effect [pdf].)
So what was Fourier’s discovery, and why is it useful? Imagine playing a note on a piano. When you press the piano key, a hammer strikes a string that vibrates to and fro at a certain fixed rate (440 times a second for the A note). As the string vibrates, the air molecules around it bounce to and fro, creating a wave of jiggling air molecules that we call sound. If you could watch the air carry out this periodic dance, you’d discover a smooth, undulating, endlessly repeating curve that’s called a sinusoid, or a sine wave. (Clarification: In the example of the piano key, there will really be more than one sine wave produced. The richness of a real piano note comes from the many softer overtones that are produced in addition to the primary sine wave. A piano note can be approximated as a sine wave, but a tuning fork is a more apt example of a sound that is well-approximated by a single sinusoid.)
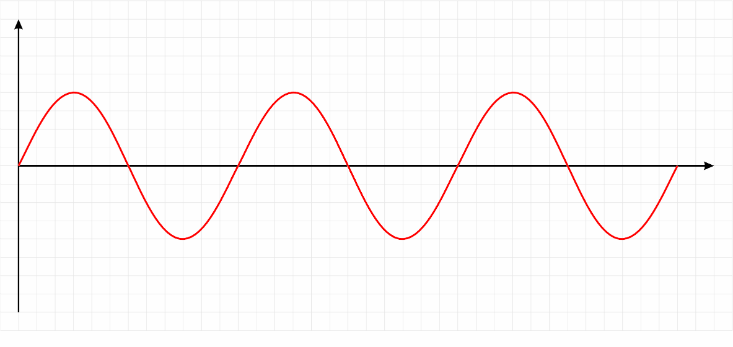
Now, instead of single key, say you play three keys together to make a chord. The resulting sound wave isn’t as pretty—it looks like a complicated mess. But hidden in that messy sound wave is a simple pattern. After all, the chord was just three keys struck together, and so the messy sound wave that results is really just the sum of three notes (or sine waves).
Fourier’s insight was that this isn’t just a special property of musical chords, but applies more generally to any kind of repeating wave, be it square, round, squiggly, triangular, whatever. The Fourier transform is like a mathematical prism—you feed in a wave and it spits out the ingredients of that wave—the notes (or sine waves) that when added together will reconstruct the wave.
If this sounds a little abstract, here are a few different ways of visualizing Fourier’s trick. The first one comes to us from Lucas V. Barbosa, a Brazilian physics student who volunteers his time to make incredible math and science animations for Wikipedia, where he goes by “LucasVB.”
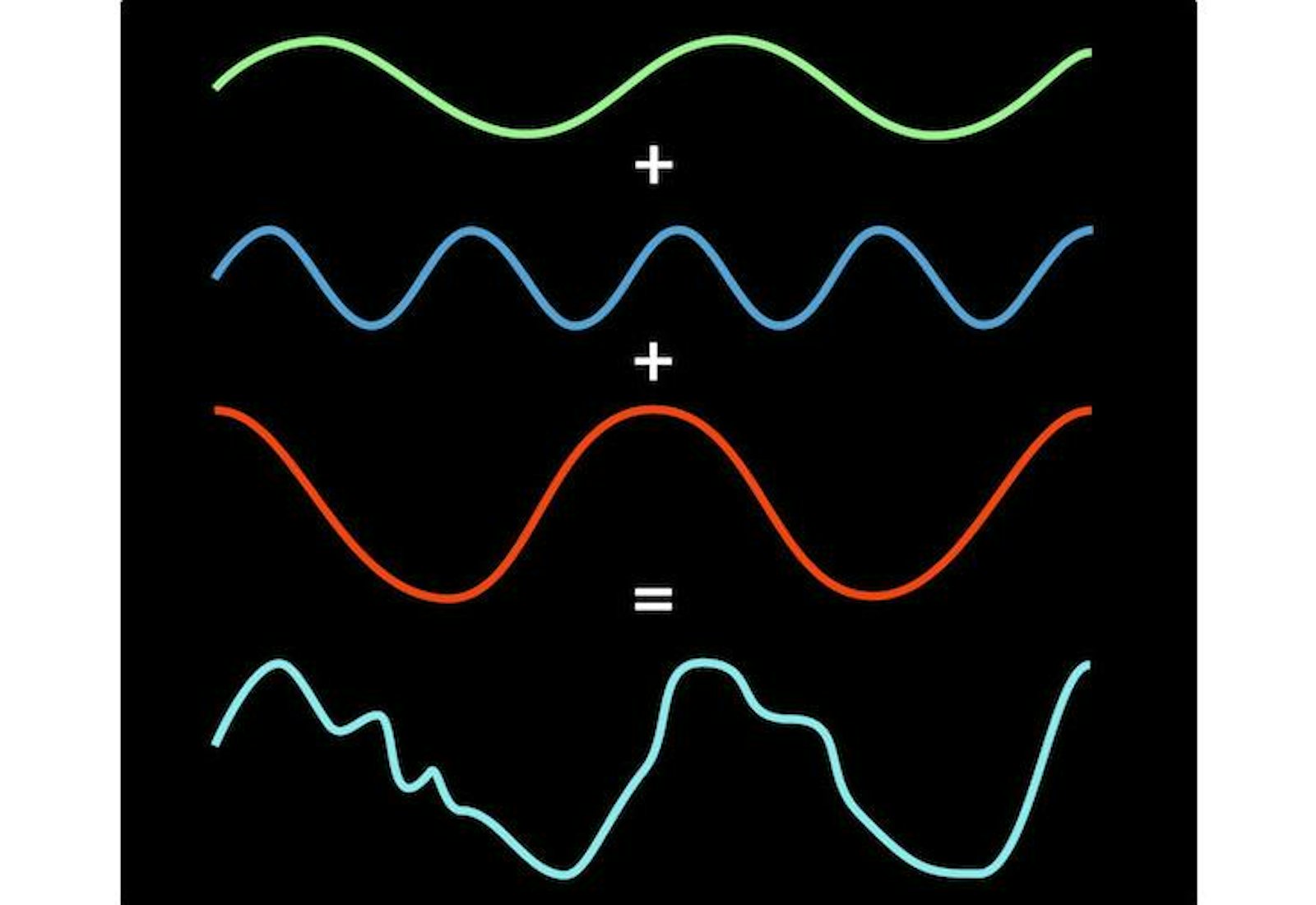
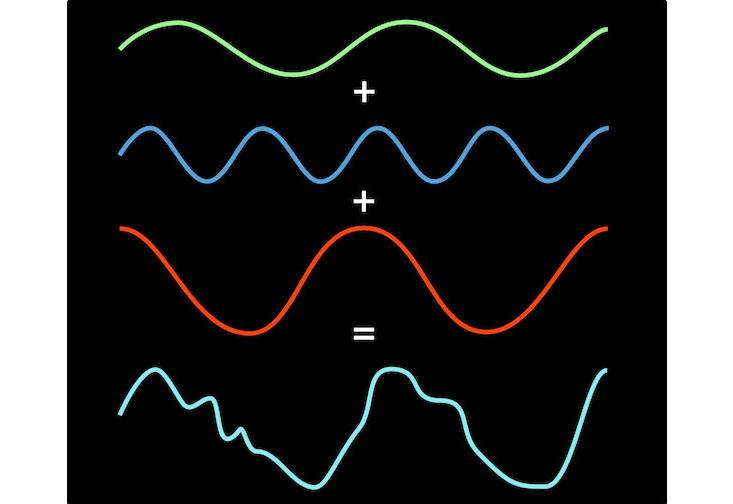
So let’s take a squarish looking wave, pass it through Fourier’s prism, and see what comes out the other side.
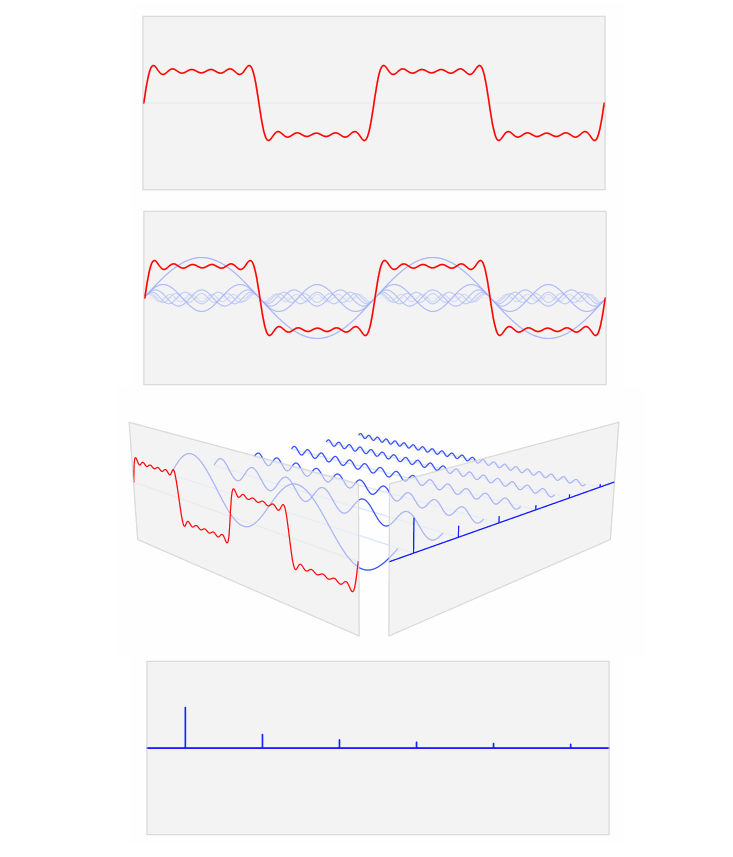
In these images (click through to Wikipedia to see it as an animation), the red squarish wave is distilled into a set of pure notes (the blue sine waves). Think of these blue waves like a mathematical ingredient list for the red wave. Pressing this analogy, the Fourier transform is a recipe—it tells you exactly how much of each note you need to mix together to reconstruct the original wave. The vertical blue lines in the animation are essentially a graph visually representing the amount of each note.
Here’s another way to think about this, provided by Matthew Henderson, or “Matthen,” a Ph.D. student at Cambridge University who also creates animated GIFs of mathematical curiosities. Matthen explains Fourier’s trick using circles instead of sine waves. This involves a set of circles of different sizes, each one centered on the edge of a bigger circle. Then the circles begin to spin, the big circles swinging the smaller ones around, and the smaller ones spinning faster than big ones. If you trace the motion of one point on the smallest circle, you can reconstruct a wave of any shape, as shown in the animation and the stills below. Again, the Fourier transform tells you how to build the wave: which circles, moving at which speeds.
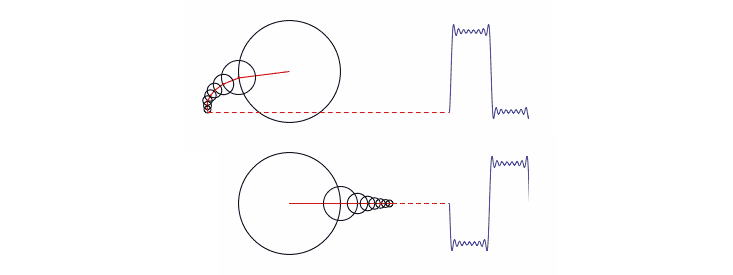
If you’re old enough to have played with a Spirograph, this idea of tracing complex patterns using wheels within wheels might be familiar to you. Here’s an interactive version of the same animation, created by LucasVB, where you can mess around and change the sizes of the circles.
To summarize, the Fourier transform tells you how much of each ingredient “note” (sine wave or circle) contributes to the overall wave. Here’s why Fourier’s trick is useful. Imagine you were talking to your friend over the phone and you wanted to get them to draw this squarish wave. The tedious way to do this would be to read out a long list of numbers that represent the height of the wave at every instant in time. With all these numbers, your friend could patiently stitch together the original wave. This is essentially how old audio formats like WAV files worked. But if your friend knew Fourier’s trick, you could do something pretty slick: You could just tell them a handful of numbers—the sizes of the different circles in the picture above. They can then use this circle picture to reconstruct the original wave.
And this isn’t just some obscure mathematical trick. The Fourier transform shows up nearly everywhere that waves do. The ubiquitous MP3 format uses a variant of Fourier’s trick to achieve its tremendous compression over the WAV (pronounced “wave”) files that preceded it. An MP3 splits a song into short segments. For each audio segment, Fourier’s trick reduces the audio wave down to its ingredient notes, which are then stored in place of the original wave. The Fourier transform also tells you how much of each note contributes to the song, so you know which ones are essential. The really high notes aren’t so important (our ears can barely hear them), so MP3s throw them out, resulting in added data compression. Audiophiles don’t like MP3s for this reason—it’s not a lossless audio format, and they claim they can hear the difference.
This is also how the smartphone app Shazam can recognize a song. It splits the music into chunks, then uses Fourier’s trick to figure out the ingredient notes that make up each chunk. It then searches a database to see if this “fingerprint” of notes matches that of a song they have on file. Speech recognition uses the same Fourier-fingerprinting idea to compare the notes in your speech to that of a known list of words.
You can even use Fourier’s trick for images. Here’s a great video that shows how you can use circles to draw Homer Simpson’s face. The online encyclopedia Wolfram Alpha uses a similar idea to draw famous people’s faces. This might seem like a trick you’d reserve for a very nerdy cocktail party, but it’s also used to compress images into JPEG files. In the old days of Microsoft Paint, images were saved in bitmap (BMP) files which were a long list of numbers encoding the color of every single pixel. JPEG is the MP3 of images. To build a JPEG, you first chunk your image into tiny squares of 8 by 8 pixels. For each chunk, you use the same circle idea that reconstructs Homer Simpson’s face to reconstruct this portion of the image. Just as MP3s throw out the really high notes, JPEGs throw out the really tiny circles. The result is a huge reduction in file size with only a small reduction in quality, an insight that led to the visual online world that we all love (and that eventually gave us cat GIFs).

How is Fourier’s trick used in science? I put out a call on Twitter for scientists to describe how they used Fourier’s idea in their work. The response astounded me. The scientists who responded were using the Fourier transform to study the vibrations of submersible structures interacting with fluids, to try to predict upcoming earthquakes, to identify the ingredients of very distant galaxies, to search for new physics in the heat remnants of the Big Bang, to uncover the structure of proteins from X-ray diffraction patterns, to analyze digital signals for NASA, to study the acoustics of musical instruments, to refine models of the water cycle, to search for pulsars (spinning neutron stars), and to understand the structure of molecules using nuclear magnetic resonance. The Fourier transform has even been used to identify a counterfeit Jackson Pollock painting by deciphering the chemicals in the paint.
Whew! That’s quite the legacy for one little math trick.
Aatish Bhatia is a recent physics Ph.D. working at Princeton University to bring science and engineering to a wider audience. He writes the award-winning science blog Empirical Zeal and is on Twitter as @aatishb.