The inside of every cell in our body is like a crowded city, filled with tracks, transports, libraries, factories, power plants, and garbage disposal units. The city’s workers are protein machines, which metabolize food, take out the garbage, or repair DNA. Cargo is moved from one place to another by molecular machines that have been observed walking on two legs along protein tightropes. As these machines go about their business, they are surrounded by thousands of water molecules, which randomly crash into them a trillion times a second. This is what physicists euphemistically call “thermal motion.” Violent thermal chaos would be more apt.
How any well-meaning molecular machine could do good work under such intolerable circumstances is puzzling. Part of the answer is that the protein machines of our cells, like tiny ratchets, turn the random energy they receive from water bombardment into the very directed motion that makes cells work. They turn chaos into order.

Four years ago, I published a book called Life’s Ratchet, which explains how molecular machines create order in our cells. My main concern was how life avoids a descent into chaos. To my great surprise, soon after the book was published, I was contacted by researchers who study biological aging. At first I couldn’t see the connection. I knew nothing about aging except for what I had learned from being forced to observe the process in my own body.
Then it dawned on me that by emphasizing the role of thermal chaos in animating molecular machines, I encouraged aging researchers to think more about it as a driver of aging. Thermal motion may seem beneficial in the short run, animating our molecular machines, but could it be detrimental in the long run? After all, in the absence of external energy input, random thermal motion tends to destroy order.
This tendency is codified in the second law of thermodynamics, which dictates that everything ages and decays: Buildings and roads crumble; ships and rails rust; mountains wash into the sea. Lifeless structures are helpless against the ravages of thermal motion. But life is different: Protein machines constantly heal and renew their cells.
In this sense, life pits biology against physics in mortal combat. So why do living things die? Is aging the ultimate triumph of physics over biology? Or is aging part of biology itself?
If there is a founding document for the modern study of aging, it may be An Unsolved Problem of Biology by Sir Peter Medawar. Medawar was a Nobel Prize-winning biologist, as well as a witty and sometimes scathing writer of essays and books. In An Unsolved Problem of Biology, Medawar pitted two explanations for aging against each other: On one hand was “innate senescence,” or aging as biological necessity. On the other was the “wearing out” theory of aging—aging due to the “accumulated effects of recurrent stress.” The former is biology, the latter physics. Innate senescence implies that aging and death are dictated by evolution to make space for younger generations.
The idea of innate senescence suggests that we have a master clock inside of us that counts down the hours of our lives. There are indeed clocks like this. The most famous are telomeres—little snippets of DNA which get shortened each time a cell divides. The study of telomeres has been controversial: It is not clear if telomere shortening is a cause or an effect of aging. Telomeres do not shorten in constant amounts—while there is a minimum amount that comes off at each cell division, they will shorten at a faster rate if the cell has been damaged through other means. Many researchers now believe that telomere shortening is more of a symptom of aging than its cause.
Life pits biology against physics in mortal combat.
Medawar himself argued for the “wearing out” theory—the physics viewpoint on aging. First, he said, it is difficult to see how natural selection could have selected for senescence, because we don’t reproduce in our elderly years and natural selection is driven by differences in reproduction rates. Second, it is unnecessary to actively kill off older individuals to keep an aging population small. Random chance can accomplish this on its own.
Medawar argued that a biological master clock for aging is unnecessary. To illustrate why, he pointed to a decidedly non-living example: Test tubes in a lab. Assume test tubes break from time to time by accident. To keep the total number of test tubes constant, a fresh supply is purchased every week. After a few months pass, how many young test tubes are there, and how many are old? If we assume that the probability of accidental breakage is independent of age (a sensible assumption), and plot the number of test tubes versus the age of each test tube, we get a concave, exponential decay curve that looks like a child’s slide. This “life curve” has a steep drop at the top, and it’s flat on the bottom.
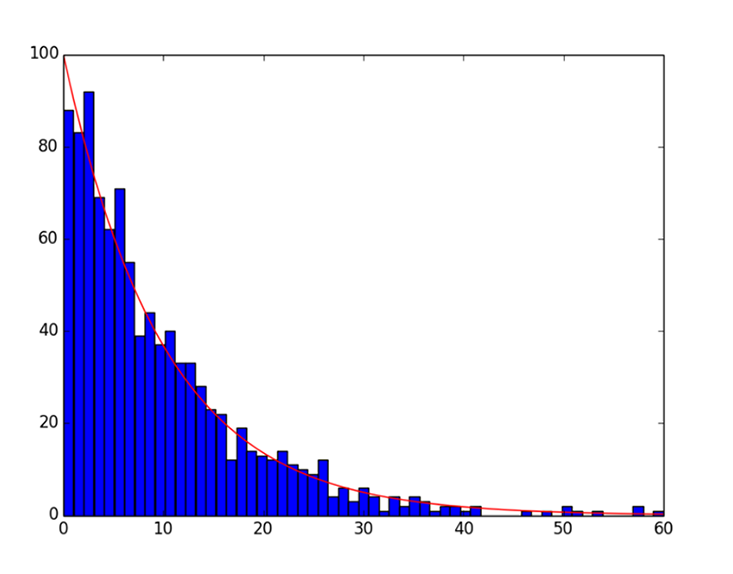
Although the test tubes are not aging (old test tubes do not break easier than young ones), the constant probability of breakage diminishes the number of old test tubes significantly. Now, suppose that humans, like test tubes, were equally likely to die at any age. The number of old people would still be small. Probability would catch up with us eventually.
The trouble is, life curves plotted for human populations do not look like Medawar’s test tube curve. They start out rather flat at the top, with a small number of losses at young age (except at birth). Then at some age, the curve suddenly drops. To obtain such a curve, we need to add another assumption to Medawar’s test tube model: Test tubes must accumulate tiny cracks over time, increasing their risk of breaking. In other words, they must age. If the risk of breaking increases exponentially, we get something called the Gompertz-Makeham law. This law matches human life curves quite well. In the language of test tubes, the law includes both a constant and an exponentially increasing risk of breakage. This exponential increase has been observed in humans, for whom the risk of death doubles every seven years after age 30.
What is the origin of this exponential increase? Thermal motion is not the only source of damage in our cells. Some regular processes, especially metabolism in our mitochondria, are not perfect and tend to produce radicals—highly reactive atoms that can damage DNA. Together, thermal noise and free radical production constitute a background risk of cell damage. The damage is usually repaired, or, if a cell is deemed beyond repair, the cell is induced to commit suicide—a process called apoptosis. Usually, a stem cell replaces it.
Eliminating cancer or Alzheimer’s disease would improve lives, but it would not make us immortal, or even allow us to live significantly longer.
Eventually, though, the damage accumulates. DNA can only be repaired when there is an intact replica to copy. Damaged proteins unfold and start sticking to each other, forming aggregates. The cell’s defense and apoptosis mechanism become compromised. “Senescent cells” start accumulating in organs, leading to inflammation. Stem cells are not activated, or become depleted. Mitochondria become damaged, reducing energy supply in cells, which is needed to power the molecular machines repairing DNA. It’s a vicious cycle—or, in technical jargon, a positive feedback loop. Mathematically, this positive feedback loop leads to an exponential increase in risk, which can explain the shape of human life curves.
The scientific literature is full of explanations for aging: Protein aggregation, DNA damage, inflammation, telomeres. But these are the biological responses to an underlying cause, which is accumulating damage through thermal and chemical degradation. To prove that thermal damage effects really do cause aging, we would need to observe humans living with different internal temperatures. This is not possible—but there are organisms that can be subjected to various internal temperatures without immediate harm. In a recent paper in Nature, a team at Harvard Medical School determined the temperature dependence of aging in the roundworm C. elegans, a simple and well-studied creature. They found that the shape of the survival curve remained essentially the same, but it was stretched or contracted as the temperature was changed. Creatures raised at lower temperature enjoyed a stretched survival curve, while worms exposed to higher temperature lived shorter lives.

What’s more, the stretch factor depended on temperature according to a pattern familiar to every scientist: It was the same as the dependence of the rate of chemical bond breakage on the temperature of random thermal motion.
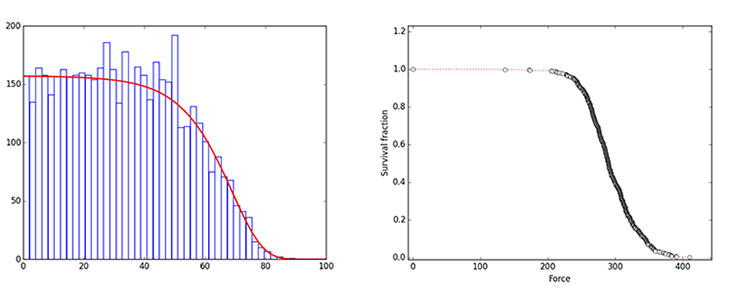
I’ve even seen a potential connection between bond breaking and human aging in my own lab. When I first encountered the Gompertz-Makeham law, it looked oddly familiar. In my lab we study the survival probability of single molecular bonds using an atomic force microscope, which can measure the minute forces acting between two molecules. In a typical experiment, we attach one protein to a flat surface and another to the tip of a small cantilever spring. We let the two proteins bind to each other, then slowly pull on the spring to apply an increasing force to the two molecules. Eventually, the bond between two molecules breaks, and we measure the force needed to achieve that breaking.
This is a random process, initiated by thermal motion. Each time we do the experiment, the breakage force is different. But the survival probability of the bonds plotted against applied force looks just like human survival plotted versus age. The similarity resonates with the C. elegans results, which suggest a possible connection between breaking protein bonds and aging—and between aging and thermal motion.
There is a vigorous discussion inside the aging research community about whether to classify aging as a disease. Many researchers studying specific diseases, cellular systems, or molecular components would like to see their favorite research subject take the mantle of “the cause” of aging. But the sheer number of possibilities being put forward refutes the very possibility. They can’t all be the cause of aging. Leonard Hayflick, the original discoverer of cellular aging, pointed out in his provocatively titled article “Biological Aging Is No Longer an Unsolved Problem” that the “common denominator that underlies all modern theories of aging is change in molecular structure and, hence, function.” The ultimate cause, according to Hayflick, is an “increasing loss of molecular fidelity or increasing molecular disorder.” This loss of fidelity and increase in disorder will manifest itself—by its very nature—randomly and therefore differently for different people. But the ultimate cause remains the same.
If this interpretation of the data is correct, then aging is a natural process that can be reduced to nanoscale thermal physics—and not a disease. Up until the 1950s the great strides made in increasing human life expectancy, were almost entirely due to the elimination of infectious diseases, a constant risk factor that is not particularly age dependent. As a result, life expectancy (median age at death) increased dramatically, but the maximum life span of humans did not change. An exponentially increasing risk eventually overwhelms any reduction in constant risk. Tinkering with constant risk is helpful, but only to a point: The constant risk is environmental (accidents, infectious disease), but much of the exponentially increasing risk is due to internal wear. Eliminating cancer or Alzheimer’s disease would improve lives, but it would not make us immortal, or even allow us to live significantly longer.
That doesn’t mean there is nothing we can do. More research into specific molecular changes in aging is needed. This may show us if there are key molecular components that are the first to break down, and whether that breakdown leads to the subsequent cascade of failure. If there are such key components, we would have clear targets for interventions and repair, possibly through nanotechnology, stem cell research, or gene editing. It’s worth a try. But we need to be clear about one thing: We’ll never defeat the laws of physics.
Peter Hoffmann is a professor of physics at Wayne State University and the associate dean of research in the College of Liberal Arts and Sciences.






























