For two weeks every summer, my parents rented a holiday apartment by the beach in Vlora, an old coastal town along the Adriatic. It was known as Aulona in Greek and Roman times, and was a special place to visit even during 1980s communist Albania. Aulona’s spirit, imprinted on the traditions, superstitions, and landscape of the place, floats outside of time. The town is guarded by a rugged terrain of high mountains, turquoise waters, and black rocks, which blend into silence at sunset. It is a place to dream absurd dreams.
My favorite evening activity was to sit on the deserted sand alone. I watched waves linger at the soundless horizon before breaking rhythmically onto the shore. As night fell, I waited until the line dividing sky and sea blurred away and all boundaries vanished. Of course everybody knew that the world beyond the horizon was strictly forbidden to those of us behind the Iron Curtain. But, sitting in the dark, I was free to imagine. Were kids on the other side of the Adriatic equally enchanted by the edge of the sky we shared? Eventually my dad would come over and, without reprimand, sit on the sand next to me. Then it was the two of us in a hushed conversation with the sky. Before long, he would speak, telling me it was time to leave, and the gentle spell of the sea and the sky would break.
Twenty years later, in 2009, I sat with a few dozen other scientists in a room at the Kavli Institute for Cosmology, Cambridge at the University of Cambridge to watch the launch of the Planck satellite. A muffled buzz filled the room with cautious excitement. Casual conversation would be interrupted by concern over pauses in the live transmission. When the countdown began, the room fell eerily quiet, and with lift-off came deep cheers and loud applause.
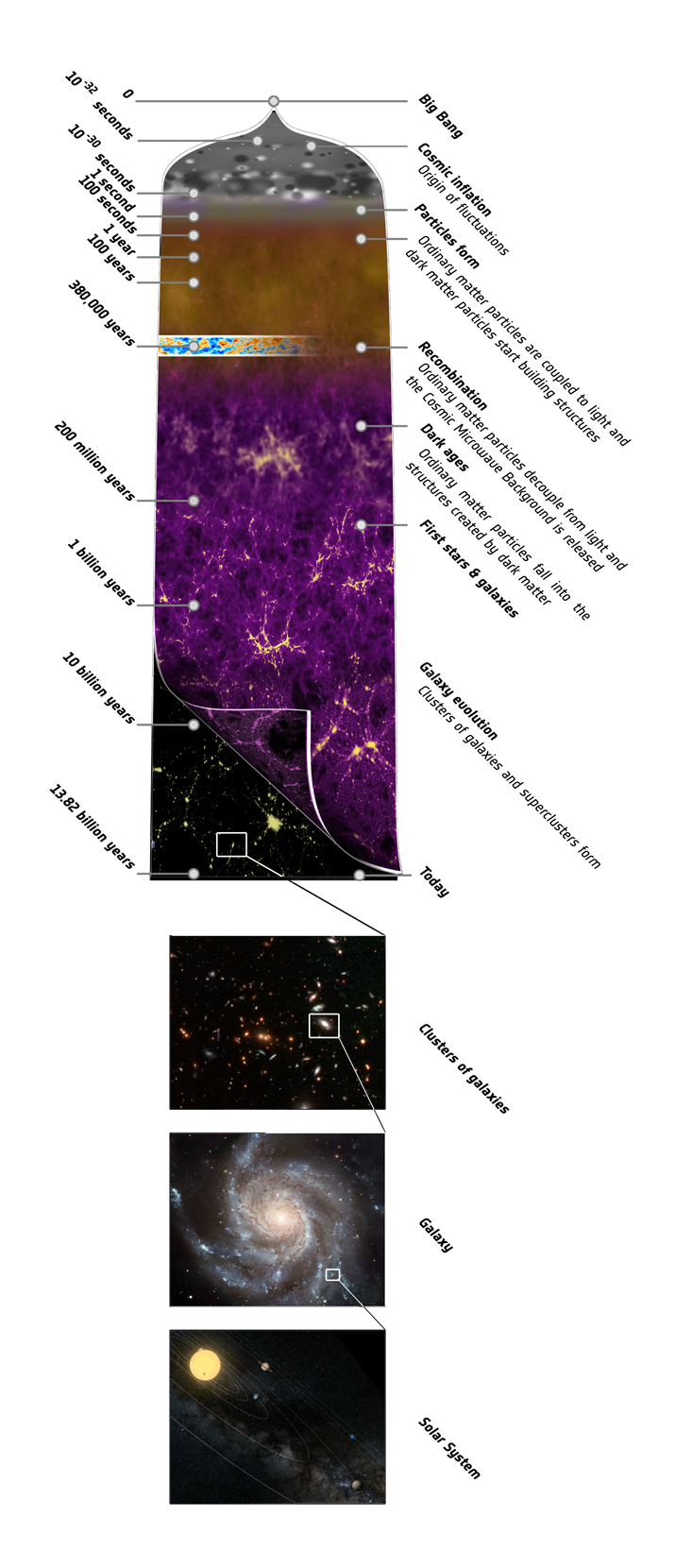
Planck was on its way to measure the gentle glow of light left over from the fiery birth of our universe, called the Cosmic Microwave Background (CMB). The CMB is a detailed fingerprint that allows us to cast our gaze onto the first few moments of our universe’s existence, and to cast light onto some very ancient questions: Where are we from, and how did we get here? (See The Standard Model.) This March, four years into its mission, the Planck collaboration released the most finely detailed map of the CMB ever measured.1 In its details was a bombshell: anomalies in the distribution of the CMB brightness that could not be the result of anything in our own universe. Here was an empirically observed hidden code pointing to a rich and vast cosmos, in which our own universe is but one humble member. The limits of our range of exploration had suddenly grown immensely. We were at the shore of the multiverse.
Contemplating the existence of other universes is not a new endeavour. From prehistoric times to the present day, this possibility has sparked the imagination of philosophers, writers, and scientists. But for most of history, it was not an idea that was taken seriously. Philosophically, it was an unnecessary complication, one that simply pushed the mystery of our origins to a new layer of reality that was unobservable in principle. And, since a theory needs to be falsifiable in order to be scientific, many scientists did not see the multiverse as “real” science. Aesthetically, too, the multiverse was not attractive. Scientists believed Nature to be simple and economical. One universe was plenty, so why bother with more? As our scientific understanding developed, however, it became clear that the multiverse is an unavoidable prediction of our theories of nature, ones that we trust and cherish: quantum mechanics, inflation, and string theory. Today, in the face of the inertia and prejudice of the past, the multiverse is finally entering the realm of serious scientific research.
If you are thinking you might have heard this narrative before, you have. From Atomists to Stoics and third century Christians, from Lucretius to Descartes, from Ptolemy to Galileo and Kant, the battle between a single universe with special origins and a collection of universes each with random beginnings has been waged for centuries. A similar battle was fought over planets and stars. In the 16th century, Copernicus took the Earth out of the center of our universe, in the face of stiff resistance from both the Church and other scientists. The multiverse might be the ultimate extension of the Copernican narrative: Even the entirety of the universe is not particularly important, but sits among infinitely many other entireties.
The multiverse narrative also has its own Copernicus: Hugh Everett who, as part of his Ph.D. thesis more than 50 years ago, had the courage to publicly pioneer the first multiverse theory by applying quantum mechanics to the whole universe. He reasoned that since the universe is tiny in its earliest moments, then it should be governed by quantum mechanics. Using wave-particle duality, he took the baby universe to be a particle behaving like a quantum wavepacket.1 He discovered a whole family of mathematical wavepacket solutions—a family of quantum universes. Knowing that we are observationally confined to a single universe, he had to wrestle with the idea that the quantum origins of our universe grant an equal chance of existence to infinitely many other universes.
The multiverse might be the ultimate extension of the Copernican narrative: Even the entirety of the universe is not particularly important, but sits among infinitely many other entireties.
Everett was not aware of any physical criterion that would discard all the solutions except one, which led him to the conclusion that the existence of many worlds is a natural consequence of quantum mechanics. His arguments were powerful enough to draw the attention of a founding father of quantum mechanics, Niels Bohr, who resisted this interpretation to the end. Everett’s academic career in physics did not make it beyond his Ph.D. studies2 and multiverse research became a cold case for more than 40 years.
The discovery of the landscape of string theory about a decade ago marked a shift in the resistance to many-universe theories. String theory is the best candidate we have for an underlying theory of nature, and operates on an 11-dimensional spacetime. But of course our universe appears to have only four dimensions: height, width, length, and time. One goal of string theory is to somehow get rid of the seven extra spatial dimensions, which it does by curling them up and making them invisible. This is analogous to a three-dimensional garden hose looking like a one-dimensional string from very far away.
But there are many ways of curling up seven dimensions and dumping their energy contents into the remaining four dimensions. At the beginning of this millennium, the mathematical exercise of exhausting all possible ways to do so led unequivocally to the discovery of a vast multitude of possible beginnings for four-dimensional universes. The energy profile of this multitude was coined the landscape of string theory. Each energy valley on the landscape was a potential site for hosting the birth of a universe through a Big Bang. The multiverse was rearing its head once again, but this time at the end of a careful, decades-long theoretical exercise.

The landscape discovery was quickly declared to be a crisis for string theory. How could the leading “theory of everything” fail to predict that there was just a single universe, and that it had the characteristics of our own? The anthropic principle, which argues that our universe is the way it is because we are here to observe it, was advertised as the way out of the crisis. I had just started my first faculty job at the time, and my mentors had suggested I focus my research on uncontroversial topics that would yield quick results, at least until I got tenure. This was well-meant advice, but nature’s most fascinating secret also had an irresistible appeal. My discomfort with the strengthening allegiance of my field to anthropic arguments also spurred me to search for a scientific formalism through which I could calculate an answer. It was a risk worth taking.
After examining the potential pitfalls and assumptions made by previous work, I concluded that the question of why our universe was selected was meaningless unless we allowed for the possibility of a variety of different beginnings. Otherwise, the question “why did we start with this universe” was indistinguishable from the answer, “all we had to start with was this universe.” The difficult step was to show how selection could be derived from the ensemble of potential states that string theory had uncovered.
I proposed that we consider a whole series of initial universes, and treat each one as a wavepacket-like particle travelling through the energy valleys of the landscape.3,4 We could then ask ourselves: How would these initial universes evolve according to the laws of quantum mechanics? This approach avoids the need for making assumptions, and embeds the Everett multiverse into the landscape of string theory. It is also, in some ways, a familiar calculation. The application of quantum mechanics to the pool of all initial universe states is very similar to how physicists calculate how electrons travel down a wire. The energy field of the chain of atoms in the wire corresponds to the chain of energy valleys in the landscape; and the electrons’ wavefunctions corresponds to the wavepackets of the initial universes.
The distribution of energies on the landscape is highly disordered, like the energies of atomic sites in an insulating material like glass or an impure, defect-filled wire. Just as electrons traveling through glass get trapped at atomic sites, wavepackets of the universe traveling across the landscape get trapped at its energy sites. If the landscape had been highly ordered into a periodic chain of low-energy sites, like a perfectly ordered conducting wire, then there would be no universe. Wavepackets would not have been localized into a single energy valley. Instead, they would have been conducted all the way through the landscape, like an electron in a good conductor.
The mark of the entanglement of our universe with others is preserved somewhere in today’s sky.
We know that our universe started in a very high-energy initial state, of about 10^25 electron volts. Given that the primordial wavepacket wandered over a disordered energy landscape, why didn’t it choose a lower-energy site? The answer is simply that, due to the quantum evolutions of the wavepackets on the landscape, high-energy initial states were the only ones that could undergo a Big Bang explosion and become large “real” universes. The evolution of these states was governed by a balance between energy obtained from the landscape, which accelerated growth, and quantum fluctuations, which decelerated growth and caused initial states to collapse into a point.
These results were considered radical at the time. But they were also encouraging, since every claim was derived from quantum equations rather than conjecture or hypothesis. For the first time we had a theory that explained why only high-energy universes like our own were selected. The theory also brought together two of the great scientific edifices of the past century, string theory and quantum mechanics, uniting them into one multiverse. But still, we did not have any testable predictions. The question became, how do you look for a multiverse?
I remember the morning when I realized that the answer was right in front of us. It was early fall in 2005, and I had spent most of the last few weeks in a state of disappointment and frustration. Every day began with optimism, and a feeling that I was close to cracking the problem. Inevitably, though, after a long evening walk spent thinking, I would come across a handful of logical flaws in the approach and become convinced the problem was unsolvable. To make matters worse, that year I had to teach a large class at 8 a.m., which is not easy for students, or for a person like myself, who works best at night. I had just finished teaching at 9 a.m. that morning and was staring blankly through a window at Starbucks when the idea hit me.
In its early moments, our universe was connected, or “entangled,” to other universes. As our universe rapidly grew and shed its quantum nature, it separated forever from all the other surviving universes in a process known as decoherence. But there is a deep principle of quantum mechanics, known as the Unitarity Principle, which states that information about a system, including a quantum wavelike universe, is never lost. This principle guaranteed that the mark of the entanglement of our universe with others is preserved somewhere in today’s sky.
Together with my collaborators, Tomo Takahashi and Richard Holman, I published a series of papers in 2006 called “Avatars of the Landscape” making concrete, empirical predictions for the signatures of other universes.5-7 Most importantly, we demonstrated that the early entanglement of our universe with the rest of the multiverse added an independent source of variation to the strength of the CMB, and to the distribution of matter around our universe, known as structure. In addition, we calculated the strength of the entanglement and showed that its effect should be observable at large scales (see The Nine Secret Codes of the Multiverse).

When we published our work, we didn’t dream that these predictions would be confirmed within our lifetimes. Amazingly, eight of the nine were tested within a scant seven years, and all were in agreement with the data. Just this March, the Planck satellite data successfully tested seven of these predictions in one fell swoop. The absence of Supersymmetry (SUSY) breaking at energies of about 1 trillion electron volts was confirmed by the Large Hadron Collider, in agreement with the ninth prediction. Only the Dark Flow prediction is still under debate, with two Planck team papers drawing conflicting conclusions. Taken together, these nine predictions represent a very stringent test of the theory, because all nine originate from a single theoretical framework. None of these predictions can be varied independently of the other eight in order to fit a particular set of data—the data must confirm them all, or the theory is ruled out.
Two previous measurements of the cosmic microwave background (COBE in 1992 and WMAP in 2007) have observed anomalies like those measured by Planck, but at a lower level of confidence. It may still turn out that the Planck anomalies are overestimated. If that turns out to be the case we will be back to square one. But if the anomalies are confirmed, and with it our first glimpse of the multiverse, we will have achieved something remarkable. Not only will we have found evidence for other universes, we will also have found the first tests of string theory, whose description of the landscape we used in our work. More broadly, the existence of multiple universes will demand that we revisit and confront some of our most cherished notions of the cosmos and develop a new ontology of reality: Do all universes live on the same underlying spacetime fabric? Was there a notion of time before our Big Bang? Can we detect universes that are not entangled with ours? What determines the laws of nature? It will be an exciting time.
In 2013, I returned to my favorite spot in Vlora, and brought my 3-year-old daughter with me. I watched her closely. She seemed excited to be there, completely carefree, and oh so happy to splash sand and water in every direction. How stunning, I thought, how far we’d come in just a generation politically, and scientifically. The usual silence was replaced by her infectious giggles. She was not curious about what lay beyond the Adriatic, because she already knew. She had been there. And to the place after that, and the one after that, all the way across the ocean. At her age, I thought I never would. But she belongs to a different generation, one that does not accept limits to imagination and discovery. As the horizon blurred and the sea and sky merged, my thoughts turned again to broken boundaries.
Laura Mersini-Houghton is an Associate Professor of Physics at the University of North Carolina at Chapel Hill.
References
1. Planck Collaboration (Ade P.A.R. et al.) Planck 2013 results. XXIII. Isotropy and Statistics of the CMB, e-Print: arXiv:1303.5083 [astro-ph.CO] (2013).
2. Byrne, P. The Many Worlds of Hugh Everett III: Multiple Universes, Mutual Assured Destruction, and the Meltdown of a Nuclear Family. (Oxford University Press, New York, 2010).
3. Mersini-Houghton, L. Can we predict Lambda for the non-SUSY sector of the landscape. Class.Quant.Grav. 22, 3481-3490 (2005).
4. Kobakhidze, A., Mersini-Houghton, L. Birth of the Universe from the Landscape of String Theory. Eur.Phys.J. C 49, 869-873 (2007).
5. Holman, R., Mersini-Houghton, L. Why the universe started from such a low entropy state.
Phys.Rev. D 74, 123510 (2005).
6. Holman, R., Mersini-Houghton, L., Takahashi, T. Cosmological avatars of the landscape I: Bracketing the SUSY breaking scale. Phys.Rev. D 77, 063510 (2006).
7. Holman, R., Mersini-Houghton, L., Takahashi, T. Cosmological avatars of the landscape II: CMB and LSS Signatures. Phys.Rev. D 77, 063511 (2006).
8. Atrio-Barandela, F. On the statistical significance of the bulk flow measured by the Planck satellite. Astronomy & Astrophysics 557, A116 (2013).






























