An Introduction to the Black Hole Institute
Fittingly, the Black Hole Initiative (BHI) was founded 100 years after Karl Schwarzschild solved Einstein’s equations for general relativity—a solution that described a black hole decades before the first astronomical evidence that they exist. As exotic structures of spacetime, black holes continue to fascinate astronomers, physicists, mathematicians, philosophers, and the general public, following on a century of research into their mysterious nature.
The mission of the BHI is interdisciplinary and, to that end, we sponsor many events that create the environment to support interaction between researchers of different disciplines. Philosophers speak with mathematicians, physicists, and astronomers, theorists speak with observers and a series of scheduled events create the venue for people to regularly come together.
As an example, for a problem we care about, consider the singularities at the centers of black holes, which mark the breakdown of Einstein’s theory of gravity. What would a singularity look like in the quantum mechanical context? Most likely, it would appear as an extreme concentration of a huge mass (more than a few solar masses for astrophysical black holes) within a tiny volume. The size of the reservoir that drains all matter that fell into an astrophysical black hole is unknown and constitutes one of the unsolved problems on which BHI scholars work.
We are delighted to present a collection of essays which were carefully selected by our senior faculty out of many applications to the first essay competition of the BHI. The winning essays will be published here on Nautilus over the next five weeks, beginning with the fifth-place finisher and working up to the first-place finisher. We hope that you will enjoy them as much as we did.
—Abraham (Avi) Loeb
Frank B. Baird, Jr. Professor of Science, Harvard University
Chair, Harvard Astronomy Department
Founding Director, Black Hole Initiative (BHI)
Black holes are mystifying objects that have captivated our imaginations since their existence was first proposed. The most striking feature of a black hole is its event horizon—a boundary from within which nothing can escape. Objects can cross the event horizon from outside to inside, but once they do, they can never cross back, nor can any information about them; anything that crosses the event horizon of a black hole is cut off entirely from the outside universe.
For many years, the existence of black holes seemed to threaten a fundamental tenet of modern physics called the second law of thermodynamics. This law helps us to distinguish the past from the future, thus defining an “arrow of time.” To understand why black holes posed this threat, we need to discuss time reversal and entropy.
Entropy and the Arrow of Time
Based on our observations, the laws of physics are (mostly) invariant under time reversal. What does this mean? Imagine a friend shows you the following video: A pendulum swings across the screen from left to right. Is this video being played normally or in reverse? Well, you have certainly seen a pendulum swing the other way before. If the laws of physics do not change under time reversal, then there is actually no way to tell: Physics looks the same with time playing forward or backward.
However, this doesn’t seem to jibe with our daily experience. Consider another video in which a bunch of ceramic shards fly up off the floor and assemble themselves into a coffee mug before coming to rest on a table. Is this video being played forward or backward? Most people would reasonably guess that the video was being played in reverse. If the laws of physics are truly invariant under time reversal, why does this intuition seem so obvious to us? The reason is that, although the laws of physics technically allow for this bizarre process to occur as shown in the video, the fact that the broken mug is made up of many, many particles means that it is essentially impossible for it to spontaneously reassemble itself.
This concept is formalized by the second law of thermodynamics, which tells us that a certain quantity, the entropy S, of any isolated system cannot decrease over time (but can increase). In other words, the change in entropy cannot be negative:
∆S ≥ 0 .
The entropy S is a statistically defined notion measuring our lack of knowledge about the underlying state of a system when we only know “macroscopic” (large-scale) information about it. By “state” here, we mean the exact configuration of each particle making up the entire system. For example, consider a box filled with gas. While we can easily measure the temperature and pressure of the gas, it is practically impossible for us to know the position and velocity of each gas particle within the box. In fact, there are many configurations of particle positions and velocities, i.e. states, that would give rise to the same temperature and pressure. The entropy encodes our ignorance of which specific state the system is actually in.
The greater the number of states that are consistent with the same temperature and pressure, the greater the entropy.
The fact that the entropy cannot decrease over time—but can increase—follows from invariance under time reversal combined with an additional property called causality. Together, these tell us that any single state of a system corresponds to exactly one state at any point in the past or in the future—no more, and no fewer. For example, one state cannot become two states at some point in the future, and two states cannot become one state.
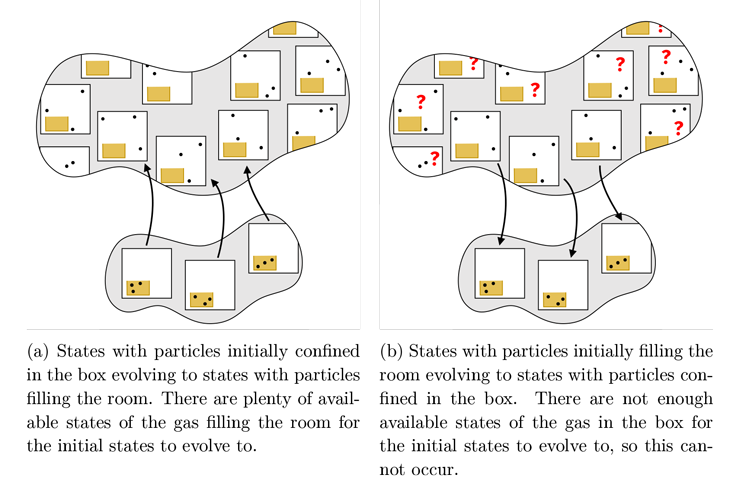
Now consider what happens when we open our box of gas into a large room. If the gas starts in the box and then flows out to fill the room, as in Figure 1a, then we can easily satisfy the rule that each initial state in the box evolves to a unique final state in the room. If we were paying close attention to every particle in the room during this process, the entropy couldn’t increase because each initial state evolves to a single final state, but we can’t keep track of so many variables; all we are able to do is measure the temperature and pressure after opening the box, and we will find that there are many, many more possible states of the gas in the whole room that are consistent with the new temperature and pressure. During this process, we lose information about the exact configuration of the particles, and thus the entropy increases. If instead the gas starts in the room and then flows into the box, as in Figure 1b, then the vast majority of the initial states in the room have nowhere to go—there simply aren’t enough states in the box. Thus, the entropy cannot decrease!
The second law of thermodynamics now gives us some sense of an “arrow of time.” Despite the fact that the laws of physics are time-reversible, the statistical notion of entropy allows us to define a forward direction for time: Time flows forward in the direction that entropy increases! This is why we feel that a video of a spontaneously reassembling coffee mug must be playing in reverse.
Black Holes and Entropy
Now, what does this all have to do with black holes? Classical black holes—the kind that would exist in a world without quantum physics—have no entropy. Physicist Jacob Bekenstein once said that these classical black holes “have no hair,” a cute phrase meaning that a classical black hole only has a few measurable properties: mass (how big it is), angular momentum (how fast it is spinning), and electric charge (like built up static electricity). When an object falls into a black hole, it contributes to these three quantities, but other than that, any information about it is lost forever.
This is a big problem for the second law of thermodynamics! If black holes truly had no entropy, then any time an object fell into a black hole, its entropy would effectively be deleted, reducing the entropy of the universe and violating the second law of thermodynamics. Without the second law of thermodynamics, why shouldn’t we see coffee mugs reassembling themselves in our day-to-day lives?
The resolution to this problem is to add quantum physics into the mix. In 1974, the late Stephen Hawking showed that in addition to the three properties above, black holes also have a temperature, now known as the Hawking temperature. The thermodynamic definition of temperature relates changes in energy to changes in entropy, so this revelation allowed Hawking to show that black holes actually do have entropy, consistent with the second law of thermodynamics. In fact, because the energy of a black hole increases when the surface area of its event horizon increases, it turns out that the entropy of a black hole is proportional to its surface area, a fact originally conjectured by Bekenstein.
Hawking’s discovery of the exact value of the Hawking temperature allowed him to compute the constant of proportionality, resulting in what is now known as the Bekenstein–Hawking (conveniently, the same letters as “Black Hole”) formula:
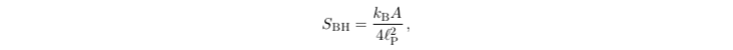
where SBH is the black hole’s entropy, A is its surface area, and kB and 𝓁P are constants known as the Boltzmann constant and the Planck length, respectively. This formula was later verified in a particular theory of black holes by the calculations of physicists Andy Strominger and Cumrun Vafa, as well as others.
The punchline is that black holes do have entropy, exactly as we had hoped, and we can tell exactly how much they have just by looking at how big they are. Once we know that black holes have entropy, we have a new form of the second law of thermodynamics that includes not only the universe outside the black hole, but also the universe within the event horizon: The total entropy, Stotal = Soutside + SBH, must never decrease. Whenever something is thrown into the black hole, the entropy Soutside of the universe outside the black hole decreases, but amazingly the surface area of the black hole, and therefore SBH, increases enough to ensure that Stotal does not get smaller. Thus, the second law of thermodynamics and the arrow of time are saved!
Andrew Turner is a graduate student in the MIT Center for Theoretical Physics, conducting research on string theory and supergravity. Originally from Ashland, Missouri, he is a graduate of Harvey Mudd College.
Alex Tinguely is a graduate student in the MIT Department of Physics, conducting fusion energy research at the Plasma Science and Fusion Center. He is originally from Fort Madison, Iowa.
This essay placed fourth in the Black Hole Institute’s essay contest.
Lead image credit: evadeb / Shutterstock






























