Kevin Hartnett
A New Law to Describe Quantum Computing’s Rise?
Neven’s law states that quantum computers are improving at a “doubly exponential” rate. If it holds, quantum supremacy is around the corner.
How Randomness Can Make Math Easier
Randomness would seem to make a mathematical statement harder to prove. In fact, it often does the opposite.
A New Approach to Multiplication Opens the Door to Better Quantum Computers
In practice, quantum computers can’t run many programs that classical computers can, because they’re not allowed to selectively forget information. A new algorithm for multiplication shows a way around that problem.
Smaller Is Better: Why Finite Number Systems Pack More Punch
Recent progress on the “sum product” problem recalls a celebrated mathematical result that revealed the power of miniature number systems.
Mathematicians Seal Back Door to Breaking RSA Encryption
Digital security depends on the difficulty of factoring large numbers. A new proof shows why one method for breaking digital encryption won’t work.
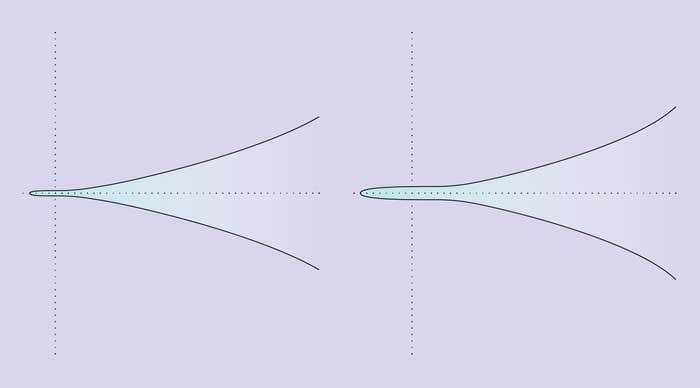
New Proof Shows Infinite Curves Come in Two Types
Alexander Smith’s work on the Goldfeld conjecture reveals fundamental characteristics of elliptic curves.
A Short Guide to Hard Problems
What’s easy for a computer to do, and what’s almost impossible? Those questions form the core of computational complexity. We present a map of the landscape.
Three Decades Later, Mystery Numbers Explained
Zeta values seem to connect distant geometric worlds. In a new proof, mathematicians finally explain why.
Robert Langlands, Mathematical Visionary, Wins the Abel Prize
Generations of researchers have pursued his “Langlands program,” which seeks to create a grand unified theory of mathematics.
How Einstein Lost His Bearings, and With Them, General Relativity
By 1913, Albert Einstein had nearly completed general relativity. But a simple mistake set him on a tortured, two-year reconsideration of his theory. Today, mathematicians still grapple with the issues he confronted.