
Is Earth unique? Once a grand philosophical question, it has, over the past two decades, become, with the discovery of thousands of planets around other stars—our cosmic cousins—a scientific one.
One way to address it is to imagine aliens, using present-day Earth technology, searching our solar system for exoplanets. Which of our eight planets would they find? The answer is Jupiter and only Jupiter. Our exoplanet-searching techniques look for the effect of planets on their host star, either through a cyclical gravitational tug, or by periodically blinking out some of the star’s light. Jupiter would only be detectable (for now) through a decades-long radial velocity survey of the Sun. We could measure Jupiter’s approximate mass and orbit. The question then becomes: How common, among known exoplanets, are systems similar to the Sun-Jupiter system?
About 1 percent. Gas giants with masses similar to Jupiter’s are found around approximately 1 in 10 stars like the Sun; however, only about 1 in 10 of those planets has a “Jupiter-like” orbit, meaning an orbit that is significantly wider than Earth’s and close to circular. Of course, we still have no data on Earths or Venuses or Saturns or Neptunes around other stars like the Sun. But it’s a start.

A second way to gauge our solar system’s uniqueness comes from Nanna Bach-Møller and Uffe Jørgensen at the Center for Star and Planet Formation in Copenhagen, Denmark. They base their argument on a relation between the number of planets in a given system and the shapes of planets’ orbits. The key piece of their analysis, published in a paper in October in the Monthly Notices of the Royal Astronomical Society, is “orbital eccentricity.” Kepler’s laws of orbital motion tell us that planets orbit their host stars following ellipses. The eccentricity of an ellipse is a measure of how stretched out it is. An ellipse with zero eccentricity is a circle; as the eccentricity approaches 1, the ellipse becomes infinitely stretched out.
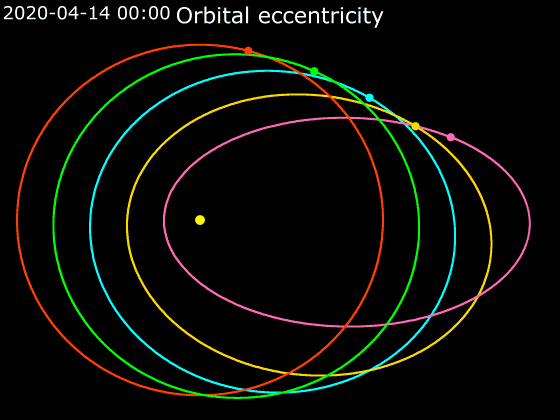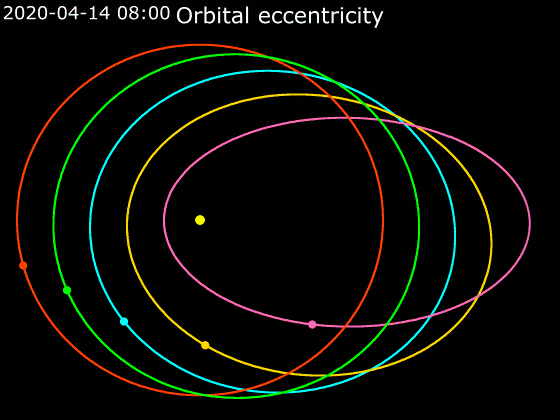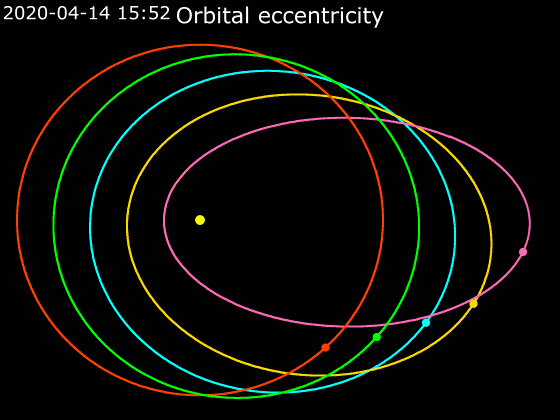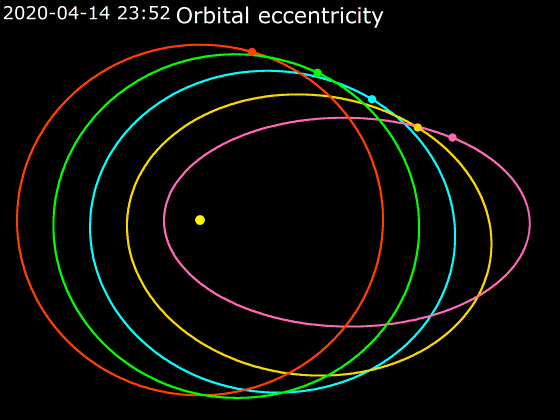
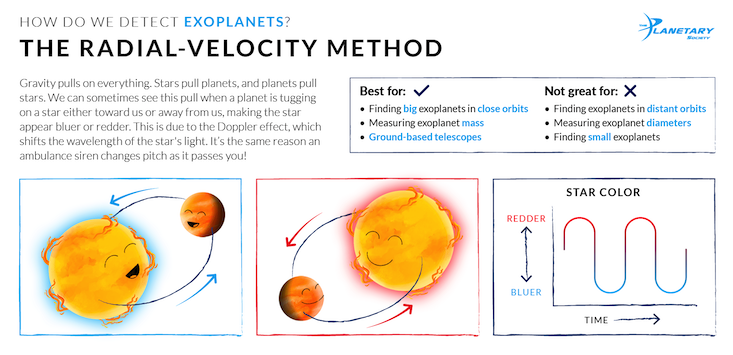
While a planet on a circular orbit moves at a constant speed around the star, planets on eccentric orbits move faster when they are closer to the star. Scientists can detect this change in orbital speed over the orbit for exoplanets using different techniques.
Bach-Møller and Jørgensen started by gathering the full sample of exoplanets for which researchers have already measured or estimated orbital eccentricities. They then calculated an “average eccentricity” for all of the planets in each system. They found that systems with more planets tend to have lower eccentricities.
This is not a big surprise. Scientists can search for exoplanets only within a limited range of orbital distances. Imagine a washing machine-sized cardboard box. How many smaller boxes can you fit inside that big box if you have to put each box inside another box (like Russian dolls)? The answer is that it depends on their shapes. If your boxes are all nice and square, then you might be able to fit a dozen or more inside each other. But if even one box is a stretched-out guitar-shaped box, then fewer boxes will be able to fit inside the big box.
It’s the same idea for orbits. Planets on circular orbits can be packed much closer together than planets on stretched-out, eccentric orbits. And the more eccentric the orbits, the fewer can fit in the range in orbital distance that we can search for exoplanets.
The researchers put numbers on orbits-inside-orbits. They found that the number of planets in a given system, versus the average eccentricity, follows a smooth relation—with just one exception. Systems with a single planet are a little bit off. These systems may have started off with many planets on near-circular orbits that, through cumulative gravitational kicks, changed their shapes until they crossed. This would have led to close gravitational scattering events that launched some planets into interstellar space!
With eight planets on relatively circular orbits, our solar system fits the trend. To give you a sense of scale, Jupiter and Saturn’s eccentricities are about 5 percent; Earth’s, about 1.7 percent; Venus and Neptune’s, both less than 1 percent. With this trend, the researchers use the occurrence-rate of exoplanets with different eccentricities to estimate how many systems have as many planets as ours. Their answer: About 1 percent, the same as we estimated using the Sun-Jupiter system.
Of course, since we have a complete census of planets (at least within Neptune’s orbit) the solar system’s “box” is much bigger than the orbital range in which exoplanets can be found. This muddles the interpretation.
When putting something in context, 1 percent is a tricky number. It’s rare enough to fall outside of the norm. Indeed, about half of all stars seem to have “super-Earth” planets on orbits closer to their stars than Mercury is to the Sun, but we don’t. One percent is also frequent enough not to be completely unexpected, and we have found some signs that our solar system isn’t a complete weirdo, including the discovery of a handful of reasonable analogs to our own Jupiter.
What does this tell us about where our system came from? The past decade has seen considerable progress in understanding how our solar system formed, yet key questions remain. What were the branching points in our planetary evolution that turned us into a 1-percent system rather than a more common one dominated by super-Earths? What made our Jupiter different compared to most of the exo-Jupiters we’ve found? And how does the growth and survival of rocky planets like Earth fit into this picture? The answer may lie in the shapes of our orbits.
Sean Raymond is an American astrophysicist working at the Bordeaux Astrophysical Laboratory in France. He also writes a blog at the interface of science and fiction (planetplanet.net), and recently published a book of astronomy poems.


























