Abstract
In the Turing test, a computer model is deemed to think intelligently if it can generate
answers indistinguishable from those of a human. We proposed a Turing-like handshake test for testing motor aspects of machine intelligence. The test is administered
through a telerobotic system in which an interrogator holds a robotic stylus and interacts with another party—human, artificial, or a linear combination of the two. Here,
we analyze and test experimentally the properties of three versions of the Turing-like
handshake test: Pure, Weighted, and Noise. We follow the framework of signal detection theory, and propose a simplified model for the interrogator human-likeness evaluation; we simulate this model and provide an assessment of the statistical power of
each version of the handshake test. Our simulation study suggests that the choice of
the best test depends on how well the interrogator identifies a human handshake
when compared with a model. The Pure test is better for intermediate and large levels
of interrogator confusion, and the Weighted and Noise tests are good for low levels
of confusion. We then present the results of an experimental study in which we compare among three simple models for a human handshake. We demonstrate that it is
possible to distinguish between these handshake models, and discuss the relative
advantage of each measure and future possible handshake models and Turing-like
tests, in measuring and promoting the design of human-like robots for robotics rehabilitation, teleoperation, and telepresence.
Introduction
As long ago as 1950, Turing proposed that the inability of a human interrogator to distinguish between the answers provided by a person and those provided by a computer would indicate that the computer can think intelligently
(Turing, 1950). The so-called Turing test has inspired many studies in the artificial intelligence community; however, it is limited to linguistic capabilities. We
argue that the ultimate test must also involve motor intelligence (that is, the ability to physically interact with the environment in a human-like fashion, encouraging the design and construction of a humanoid robot with abilities indistinguishable from those of a human being). It was suggested that robots that
appear as more human-like may be perceived as more predictable; and thus,
people are more likely to feel comfortable while interacting with them (Hinds,
Roberts, & Jones, 2004); naturally, when physically interacting with a robot, such human-likeness is even more important. However,
an ultimate Turing-like test for motor intelligence
involves an enormous repertoire of movements. In this
paper, we discuss the methodology of performing a
reduced version of the ultimate test, which is based on
the one-dimensional handshake test proposed earlier
(Karniel, Avraham, Peles, Levy-Tzedek, & Nisky, 2010;
Karniel, Nisky, Avraham, Peles, & Levy-Tzedek, 2010).
In this reduced version of the Turing-like test for motor
intelligence, a model of a human handshake is considered human if it is indistinguishable from a human
handshake.
A true understanding of the motor control system could be demonstrated by building a humanoid robot.
The handshake is of interest not merely as a reduced
version of the ultimate humanoid test, but also due to its
bidirectional nature, in which both sides actively shake
hands and explore each other. Motor control research
has concentrated on hand movements (Flash & Hogan,
1985; Karniel & Mussa-Ivaldi, 2003; Morasso, 1981;
Shadmehr & Mussa-Ivaldi, 1994; Shadmehr & Wise,
2005; Wolpert & Ghahramani, 2000), generating a variety of hypotheses which could be applied to generate a
humanoid handshake. In addition, the subjective perception of manual mechanical interaction with the external
world was studied extensively (R. Friedman, Hester,
Green, & LaMotte, 2008; Jones & Hunter, 1990, 1993;
Srinivasan & LaMotte, 1995; Tan, Durlach, Beauregard,
& Srinivasan, 1995). Last but not least, the greatest progress in telerobotic (Hannaford, 1989; Niemeyer &
Slotine, 2004; Yokokohji & Yoshikawa, 1994) and haptic
(Biggs & Srinivasan, 2002; El Saddik, 2007; Okamura,
Verner, Reiley, & Mahvash, 2011) technologies involves
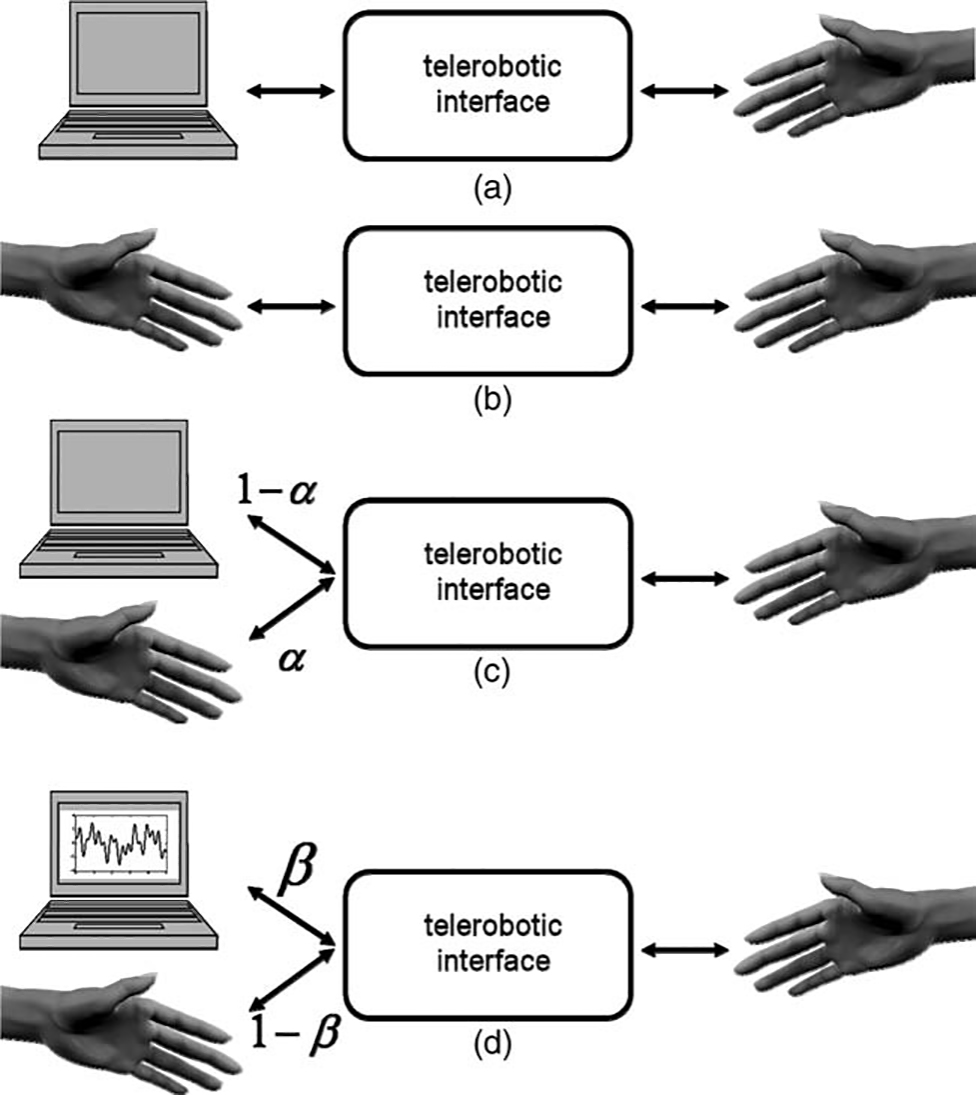
arm movements. The telerobotic interface is necessary to
grant the human–computer discrimination significance,
much as the teletype was necessary to hide the computer
from the questioning human in the original Turing test.
Handshaking has been discussed in the social context
(Chaplin, Phillips, Brown, Clanton, & Stein, 2000;
Stewart, Dustin, Barrick, & Darnold, 2008), but the development of artificial handshake systems is still in its
infancy (Bailenson & Yee, 2007; Jindai, Watanabe,
Shibata, & Yamamoto, 2006; Kasuga & Hashimoto,
2005; Kunii & Hashimoto, 1995; Miyashita & Ishiguro,
2004; Ouchi & Hashimoto, 1997; Sato, Hashimoto, &
Tsukahara, 2007; Wang, Peer, & Buss, 2009), and state-of-the-art studies mostly explore very basic forms of haptic interaction and collaboration (Bailenson & Yee,
2008; Bailenson, Yee, Brave, Merget, & Koslow, 2007;
Durlach & Slater, 2000; Gentry, Feron, & Murray-Smith, 2005; Groten et al., 2009; Hespanha et al.,
2000; J. Kim et al., 2004; McLaughlin, Sukhatme, Wei,
Weirong, & Parks, 2003). The proposed Turing-like
handshake test can be useful in identifying the aspects of
the theories that are essential for producing a human-like
handshake movement. In general terms, we assert that a
true understanding of the motor control system could
be demonstrated by building a humanoid robot that
moves and applies forces that are indistinguishable from
a human. Therefore, a measure of our distance from such
a demonstration could be most useful in evaluating current scientific hypotheses and guiding future neuroscience research.
Moreover, understanding the unique properties of
healthy hand movement is important for clinical applications. For example, it will allow clinicians to discriminate
between unimpaired hand movements and movements
that are generated by motor-impaired individuals, such
as cerebral palsy patients (Roennqvist & Roesblad,
2007; van der Heide, Fock, Otten, Stremmelaar, &
Hadders-Algra, 2005) and Parkinson patients (van Den,
2000), among others. Such automatic discrimination
can be useful for diagnosis as well as for assessment of
treatment affectivity.
The evaluation of human-likeness of haptic interaction
with robotic manipulators has received little, yet growing, attention in recent years. Variable impedance control of a robotic manipulator was compared to constant
impedance control in terms of perceived human-likeness
(Ikeura, Inooka, & Mizutani, 1999) and human-like
movements (Rahman, Ikeura, & Mizutani, 2002). The
effect of visual and haptic rendering strategies on plausibility of social interaction was studied in the context of
handshaking (Wang, Lu, Peer, & Buss, 2010). A recent
study explored the human-likeness of feedforward- and
feedback-based models for haptic interaction partners
(Feth, Groten, Peer, & Buss, 2011).
In our previous studies, we presented initial exploration of the Turing-like handshake tests (Avraham, Levy-
Tzedek, & Karniel, 2009; Karniel, 2010; Karniel, Nisky, et al., 2010), and proposed three different methodologies for assessing the human likeness of a handshake
model (Karniel, Avraham, et al., 2010): (1) a Pure test,
(2) a Weighted test, and (3) a Noise test. The methodologies are similar in the general experimental architecture:
a human interrogator shakes hands with another human,
with computer software, or with a combination of the
two. The handshake is performed through a telerobotic
system, as depicted in Figure 1. However, the three versions of the test are conceptually different: in the Pure
test, handshake models are compared against human
handshakes; in the Weighted test, combinations of a
model and human handshake with different weights are
compared; in the Noise test, models are compared
against human handshakes combined with noise.

In the current paper, we set out to explore the differences between these three versions of the Turing-like
handshake test in a simulation study based on the preliminaries from signal detection theory (SDT). To further explore the methodological differences between
these three versions, we present an experimental study
that uses all three methods to compare between three
simple models for a human handshake. The main contribution of this work is methodological, and hence, we
chose very simple and primitive models for a human handshake, and did not incorporate into the models any
of the abundant recent findings in human motor control.
We begin the paper with a brief introduction to SDT
and psychometric function evaluation. We
then describe the three proposed versions of the Turing-
like handshake test; present our simulation
study; and the experimental comparison of
three models for a human handshake using all three
Turing-like tests. We conclude the paper
with a discussion of the simulated and experimental
results. Part of the content has
been also reported in Karniel, Avraham et al. (2010).
However, here we add more definitions and assumptions
required for the simulations in the following sections;
moreover, the analysis and simulations reported are unique to this paper, and were only
partly presented in an abstract form (Avraham, Nisky, &
Karniel, 2011).
Preliminaries in Psychophysics—Signal
Detection Theory and the Psychometric
Function
SDT is a mathematical framework for analyzing
human decision-making in perceptual and cognitive tasks, that makes the role of decision processes explicit
(Abdi, 2007b; Gescheider, 1985; Lu & Dosher, 2008;
MacMillan, 2002). In particular, the theory provides
computational tools for estimating the sensitivity and
response bias of the participant in the task. In the original notion of SDT, the task is to categorize ambiguous
stimuli which can be generated either by a known process (signal) or be obtained by chance (noise); namely, a
yes–no task. In another paradigm, the two-alternative
forced choice (2AFC), the task is to sort two different
stimuli into categories. In the current paper, we use the
2AFC paradigm in which the two stimuli in each trial are
two different handshakes, and the categories are ‘‘more
human-like’’ and ‘‘less human-like.’’
According to SDT, the response of the participant
depends upon the intensity of a hidden variable—a continuously variable internal representation—and the participant makes the decision based on some objective criterion with regard to this representation. In the 2AFC
paradigm, in each trial, the participant compares the
magnitudes of the internal representations of both stimuli, and chooses the stimulus that generates the greater
internal response to belong to a category with a higher
expected internal response. Importantly, the scale of internal representations is arbitrary, and does not necessarily correspond to some physical property of the stimulus.
Errors arise when the distributions of the categories
overlap, and the proportion of the correct responses is
used to estimate the extent of overlap between the internal representations of the different categories. In our
case, the hidden variable is internal representation of
human-likeness of a handshake, and we will designate it
as h in the remainder of the paper. SDT, as a theoretical
framework, does not specify the distribution of the internal representation; however, in most applications, the
distributions of the representations are assumed to be
Gaussian, and often, the variances of the different categories are assumed to be equal. We follow these common assumptions, and assume that h~ N (μ, σ); namely, the probability density function of the internal
representation of human-likeness of a handshake is:
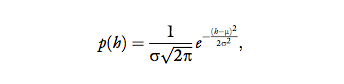
where μ is the expected human-likeness of a specific
handshake on an arbitrary scale, and σ is the variance of
the internal representation.
A tightly related method of quantifying performance
in psychophysical task is the psychometric curve. A common experimental design for fitting such a curve is the
method of constant stimuli: the task is similar to the classic description of SDT, but a standard stimulus (usually
drawn from the middle of stimuli range) is presented in
each trial together with one of n5 comparison stimuli.
The participant labels each as larger or smaller than the
standard, and the function that quantifies the probability
of answering ‘‘comparison stimulus was larger’’ is the
psychometric function. The presence of standards does
not temper the analysis because it gives no information
regarding which response is appropriate (MacMillan,
2002).
The general form of the psychometric function is:
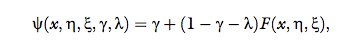
where x is the physical property of the stimulus, and the
shape of the curve is determined by the parameters (η, ξ, λ, ϒ) and the choice of a two-parameter function F, typically, a sigmoid function (Wichmann & Hill, 2001). The
rates of lapse are ϒ and λ—incorrect response regardless
of the difference between stimuli intensity, and η and ξ
determine the shift and the slope of the sigmoid function, respectively. The choice of a specific function is
determined by an assumption about the distribution of
the internal representation, by how its parameters
change with stimulus intensity, and by what the decision
rule is (Garcia-Perez & Alcala-Quintana, 2011). Under
the assumption in Equation 1, the psychometric function will have a logistic form, namely,
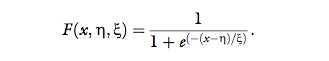
The 0.5 probability point is interpreted as the point of
subjective equality (PSE)—the comparison stimulus intensity that is perceived equal to the standard—a measure of bias, and it is estimated as the inverse of the sigmoid function at the 0.5 threshold, F-1 (0.5). When the
assumption in Equation 1 is not reasonable, it is still
possible to estimate the PSE correctly by fitting other sigmoid functions, or using distribution-free methods,
for example, Spearman-Kraber (Miller & Ulrich, 2001).
Three Turing-like Tests—Methods to
Model Human-Likeness Grade
Assessment
Following the original concept of the classical
Turing test, each experiment consists of three entities:
human, computer, and interrogator. Two volunteers
participate in the experiment: human and interrogator.
Throughout the test, each of the participants holds the
stylus of one haptic device and generates handshake
movements (see Figure 1). In all three methods (Pure,
Weighted, and Noise), each trial consists of two handshakes, and the interrogator is asked to compare between
the handshakes and answer which of them feels more
human. Based on the answers of the interrogator, we calculate a quantitative measure for the human-likeness of a
handshake model, the model human-likeness grade
(MHLG). This grade quantifies the human likeness on a
scale between 0 and 1. The computer is a simulated
handshake model that generates a force signal as a function of time and the 1D position of the interrogator’s
haptic device (xinter (t)) and its derivatives:
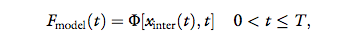
where Φ[xinter (t), t] stands for any causal operator, and
T is the duration of the handshake.
The force feedback to the human is generated purely
by the interrogator to preserve, as much as possible, the
natural characteristics of the human handshake movement. The nature of the force applied on the interrogator is the key difference between the three methods that
are discussed in this paper. In general, it is either pure
human, pure computer, or a combined human and computer handshake (see Figure 2).
Pure Turing-like Test
The Pure Turing-like test is the most similar to the
original notion of the Turing test for intelligence. In
each trial, the interrogator is presented with a pure computer handshake, Figure 2(a), and a pure human handshake, Figure 2(b). Namely, the force that is transmitted
to the interrogator is
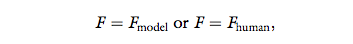
where Fmodel is defined in Equation 3, and Fhuman is a
function of the real-time position and/or force applied
by the human and its derivatives, and its exact implementation depends on the teleoperation architecture. If we
wish to compare nm models in a single experiment, each
block consists of nm trials, one trial per model. Each
experiment consists of N blocks, such that each computer handshake is repeated N times. The main purpose
of the current study is to compare different methods for
human-likeness assessment, and therefore, we choose N
such that the total number of trials will be identical between different methods. In general, the choice of N
affects the statistical power of the test, and should be
determined according to the desired significance and
power according to pilot studies. An analysis of statistical
power of this test and how it is related to the number of
blocks is presented at the end of this section.
For each model, we calculate the proportion of handshakes in which the interrogator chooses the computer
handshake (m) over the human handshake (h) as more
human-like, pm>h. This is an estimate of the probability
of the interrogator to decide that the modeled handshake is more human than the human handshake. We
follow SDT, and assume that after a completion of the
probing phase of trial i, internal representations of
human-likeness are formed for each of the individual
handshakes, him and hih (where the superscripts m and h
indicate model and human handshakes, respectively).
With this formulation, pm>h is an estimate of the probability p(him > hih). When the model is indistinguishable
from a human, E(pm>h) = p(him > hih) = 0:5. We calculate the MHLG of the Pure test (MHLGp) by multiplying this estimation by two, such that MHLGp = 0
means that the model is clearly non-human-like, and
HMLGp = 1 means that the tested model is indistinguishable from the human handshake:
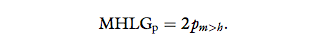
Since the human handshake is the most human by definition, MHLGp is cut off at 1.
Intuitively, when the interrogator is very good at
identifying the human handshake when compared with
any computer handshake, this test will be ineffective in
grading the different models relative to each other.
This is because SDT is based on the assumption that mistakes are happening, and is not applicable otherwise.
Therefore, we designed two additional versions of the
Turing-like test. In both versions, the main idea is to
present the interrogator with handshakes that are a mixture of human-generated and computer-generated handshakes, as shown in Figure 2(c–d). This increases the
level of confusion of the interrogator, and allows an
effective comparison between different models, even if
each of the models, by itself, is quite far from being
human.
Weighted Turing-like Test
In the Weighted Turing-like test, the interrogator
is always presented with a combination of a human and a
computer handshake, as shown in Figure 2(c). Namely,
the force that is transmitted to the interrogator is:
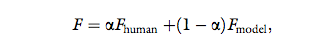
where Fmodel and Fhuman are defined similarly to the definition after Equation 4. The exact value of α is determined according to a predefined experimental protocol.
As in the Pure test, a single trial consists of two handshakes. In each trial, in one of the handshakes—the
comparison stimulus—the interrogator interacts with a
combination of forces according to Equation 6 with α = αcomparison, where αcomparison is one of n5 equally
distributed values from 0 to 1, for example,
αcomparison = {0, 0.2, 0.4, 0.6, 0.8, 1}. The other
handshake—the standard stimulus—is also a combination of forces, but with a fixed weight α = αstandard = 0.5,
generated online from the human and a reference model,
which is chosen before the experiment.
In each experiment, we assess the human-likeness of
nm – 1 test models and a reference model. In the trials
in which we assess the human-likeness of the reference
model, the interrogator is presented with the same
model in both handshakes, but with different weights,
and thus, these trials serve as the control. Each experimental block consists of nmn5 trials comprising each of
the n5 linear combinations of the model and the human
for each of the nm model comparisons.
The order of the trials within each block is random
and predetermined. Each experiment consists of nb
blocks, such that each combination is repeated nb times.
We choose the number of blocks nb, such that, similarly
to the Pure test, each stimulus model is presented to the
subject in N = nbn5 trials.
The next step in assessment of the human-likeness of
each model is to fit a psychometric curve, Equation 2, to
the probability of the interrogator to answer that a com-
parison handshake is more human-like as a function of
x = αcomparison – αstandard (see Figure 11 for an example of psychometric curves
derived from experimental data). We assume that a higher weight of a human handshake component in a
combined handshake yields a higher probability to
choose a handshake as more human-like. Thus, this
probability approaches one as the difference
αcomparison – αstandard > 0 becomes larger, and zero
for a larger difference in the opposite direction,
αcomparison – αstandard < 0. This is a necessary assumption
for the Weighted test, and hence, should be validated
for each class of new models that are tested with it. This assumption was validated in our previous studies
(Avraham et al., 2009; Karniel, 2010; Karniel, Nisky
et al., 2010) as well as in the experimental study of the
current paper in the “Experiment” section. However, in the general case,
there might be models for a human handshake that feels
human-like when presented alone, but will do poorly
when combined with a human handshake, and vice versa.
In these cases, the Weighted method should not be used.
The PSE indicates the difference between the
αcomparison and αstandard for which the handshakes are perceived to be equally human-like. We use the estimated
PSE for calculating MHLGw according to:
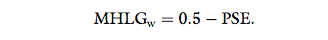
Thus, a model that is perceived to be as human-like as
the reference model yields the MHLGw value of 0.5.
The models that are perceived as least or most human-like yield possible MHLGw values of 0 or 1, respectively.
Therefore, MHLGw is cut off at 0 and 1.
The Weighted test is highly dependent on the successful fitting of the psychometric function. In Wichmann
and Hill (2001), it was shown that the fitting process is
most effective when the stimulus intensities are distributed symmetrically around the PSE, at low as well as
high performance values. Therefore, the Weighted
method will be most effective for a reference model that
is similar or slightly less human than the tested models.
Noise Turing-like Test
The main methodological concern in using the
Weighted test is the fact that it is not necessary that the
model that is perceived to be most human-like when
combined with a human handshake is actually most
human-like when presented alone. Therefore, we
designed a third method for the assessment of computer models’ human-likeness. In the Noise Turing-like
method, the interrogator is presented with either a computer handshake, as in Figure 2(a), or a human handshake combined with a noise, as in Figure 2(d). This
noise is chosen such that the resultant handshake is perceived to be the least human-like possible, and such that
the human handshake is perceived as less human as the
weight of noise increases. This allows for an effective
comparison of a pure model handshake with a human
handshake corrupted by different levels of noise. The
idea is that if more noise is required for degrading the
human handshake such that it will be indistinguishable
from the model, then the model is less human-like. Such
an approach was suggested in the context of measuring
presence in virtual environments according to the
amount of noise required to degrade the real and virtual
stimulation until the perceived environments are indiscriminable (Sheridan, 1994, 1996).
The protocol of the Noise Turing-like handshake test
is similar to the Weighted protocol. In each trial, the
interrogator is presented with two handshakes. In one of
the handshakes—the standard stimulus—the interrogator interacts with a computer handshake model. The
other handshake—the comparison stimulus—is a handshake that is generated from a combination of the
human handshake and noise. In the current study, we
chose the noise as a mixture of sinus functions with frequencies above the natural bandwidth of the human
handshake (Avraham et al., 2009; Avraham, Levy-Tzedek, Peles, Bar-Haim, & Karniel, 2010; Karniel,
2010; Karniel, Nisky et al., 2010), but the general
framework is flexible, and any other function can be used
instead, as long as it is indeed not human-like. The comparison handshake force is calculated according to:
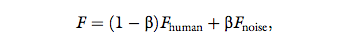
where β is one of n5 equally distributed values from 0 to
1, for example, β = {0, 0.2, 0.4, 0.6, 0.8, 1}. Similar to
the previous tests, at the end of each trial, the interrogator is requested to choose the handshake that felt more
human-like.
The rest of the methodological details, including fitting of the psychometric function, are similar to the
Weighted test. However, the psychometric curve is now fitted to the probability to choose the standard handshake as more human-like as a function of β, the relative
weight of noise in the comparison handshake. Namely,
for a model that is indistinguishable from human, the
expected PSE is 0. For a model that is as human-like as
the noise function (hence, the least human-like model),
the expected PSE is 1. Therefore, the MHLGn is calculated according to:
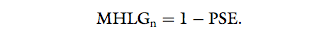
Thus, models that are perceived as the least or the most
human-like possible yield MHLGn values of 0 or 1,
respectively, and the estimations of MHLGn are cut off
at 0 and 1.
Simulation
Intuitively, by design, the different methods that
are described in the previous section are expected to
be useful for different levels of sensitivity of the interrogator to the difference between human-generated and
computer-generated handshakes. In the current section,
we set out to quantify the difference between the
approaches in terms of statistical power of each method
under various conditions.
Methods
In order to build a simulation of different psychophysical approaches, we must make an assumption about
the decision process underlying the answers of the interrogator. In the current work, we do not explore the decision process, and therefore, we make assumptions that
will allow us to explore the different experimental methodologies. The guiding principle behind our assumptions is maximal simplicity. Therefore, we do not simulate the actual handshake, and instead we simulate a
simplified decision process.
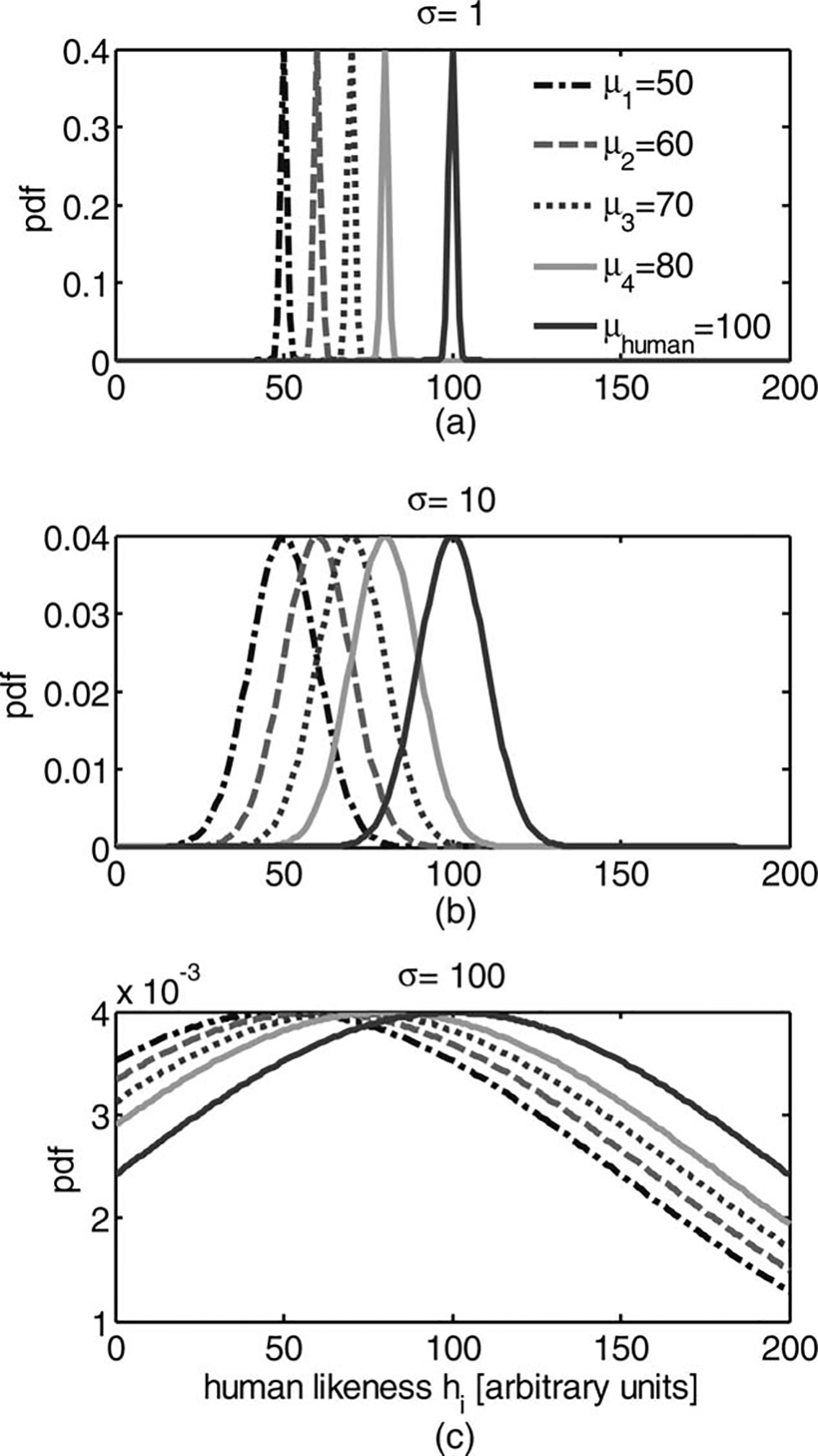
We follow the general framework of SDT, and assume
that after a completion of trial i, an internal representation of human-likeness (hi) is formed, and we assume
Gaussian distribution for this internal representation, as
specified in Equation 1. We also assume that for all computer, human, and combined handshakes, this distribution has identical standard deviation, but different means, and that these means are consistent across subjects. The mean of this distribution is the actual human-likeness of the handshake and the variance represents the
confusion level of the interrogator, namely, decision variance (see Figure 3). We simulate the decision of the
interrogator by choosing a random variable hi from the appropriate distribution for each of the handshakes in a
single trial, and answering according to the magnitude
of hi. The process is repeated for a number of trials, and
the appropriate MHLG is calculated according to the
simulated answers of the interrogator. We tested five
models with μm = {50, 60, 70, 80, 100} means of internal representation of human-likeness of the models, and
compared them to a completely human handshake, for
which the mean of the internal representation μhuman =100. This simulation was repeated for different decision
standard deviation values, σ = {1, 10, 30, 50, 70, 90}.
We repeated the process 10 times to estimate the variability of MHLG for different repetitions of the simulation, so as to simulate repetition of the experiment with
different subjects. This procedure also allowed us to perform a one-sided, paired t-test, and determine whether
the MHLG of two simulated models are statistically significantly (p < 0.05) different.
Pure Test Simulation
For each model, we
repeated 80 trials where a single sample from a random
variable hm ~Ν(μm σ) was compared to a sample from
hh ~ Ν(μhuman σ). We calculated pm>h, the proportion
of trials in which him > hih, and used it to calculate
MHLGp according to Equation 5.
Weighted Test Simulation
The
Weighted Turing-like test is based on the assumption that
a higher weight of the human handshake component in a
combined handshake yields a higher probability of choosing a handshake as more human-like. We incorporated
this assumption into the simulation by choosing the mean
value for human-likeness of a combined handshake as:
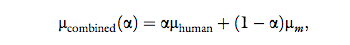
without changing the standard deviation of the decision
variable. We chose the least human-like model, μm = 40,
as a reference model, and each of the tested models, μm = {50, 60, 70, 80, 100}, as comparison models, and performed simulation of 10 blocks per interrogator. Within
each block, for each model, αcomparison was assigned with
eight equally distributed values from 0 to 1: αcomprison =
{0, 0.142, 0.284, 0.426, 0.568, 0.710, 0.852, 1}, and
αstandard = 0.5. As in the Pure test simulation, each trial was simulated such that a single sample from a random variable hcomparison ~ Ν(μcombined(αcomparison)σ, ) was
compared to a sample from hstandard
~ (μcombined (αstandard), σ). Note that 10 blocks of eight
levels of αcomparison yield a total of 80 trials per model,
similar to the Pure test. This is important for comparability of the methods. At the end of the simulation, for each
level of αcomparison, we calculated pc>s(αcomparison), the
proportion of trials in which hcomparison > hstandard for
that particular level of αcomparison. We used the Psignifit
toolbox version 2.5.6 for MATLAB1 to fit a logistic psychometric function (Wichmann & Hill, 2001) to the
simulated answers of the interrogator and extract the
PSE, and used it to calculate MHLGw according to
Equation 7. In the special case when pc>s(αcomparison) >
0.5 for all αcomparison, the fitting of the psychometric
function is not reliable. However, since this only occurs for
models that are very human-like when compared with the
reference handshake, we set MHLGw = 1 in these cases.
Noise Test Simulation
The simulation of
the Noise test was similar to the Weighted test, with a
few differences. We assumed that the noise that we add
to the human handshake is equivalent to combining the
human handshake with the least human-like model possible, namely, μnoise = 40, and therefore:
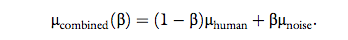
Within each block, for each model, β was assigned with
eight equally distributed values from 0 to 1: β =
{0, 0.142, 0.284, 0.426, 0.568, 0.710, 0.852, 1}.
As in the previous simulations, each trial was simulated
such that a single sample from a random variable
hstandard ~ Ν(μm, σ) was compared to a sample from
hcomparison ~ (μcombined(β), σ). At the end of the simulation, for each level of β, we calculated ps>c(β), the proportion of trials in which hstandard > hcomparison. We
extracted the PSE from a psychometric function and calculated MHLGn according to Equation 8.
Statistical Power Analysis
To compare
the performance of each of the tests for different levels of Δμ and different levels of confusion of the interrogator,
we performed a systematic statistical power and size of
effect analysis by means of Monte Carlo simulations
(Abdi, 2007a). For each of the tests, we repeated 100
simulations, in which we repeated five calculations of the
MHLG for each of the models μm = {50, 52, 54, … ,
96, 98, 100}. Then, we performed a one-sided paired
t-test between the MHLG of the worst model (μm = 50)
and each of the other models. This choice of particular
comparisons was arbitrary, and actually, once an MHLG
for each model was calculated, any pair of models could
be compared. The power of each Turing-like test is the
proportion of the simulations in which the difference in
MHLG was significant at the .05 significance level, and
the size of the effect is the mean difference between the
MHLGs that were compared. In the current paper, we
state that a test has sufficient statistical power when this
proportion is 0.8 (Cohen, 1988, 1992). Each of these
procedures was repeated for different levels of standard
deviation of hi, σ = {1, 4, 7, 10, … , 97, 100}.
Next, we used a similar procedure to assess the power
of the different tests in detection of difference between
the human-likeness of very similar models, Δμ = 6, a difference which is small enough when compared with
mean values of 50–100, but large enough to be a significant difference for the smallest level of interrogator
confusion. Here, instead of comparing all models to the
least human-like model, we compared models with similar levels of human-likeness. The idea here was to explore
whether the performance of the test depends on how
human-like are these two similar models; namely,
whether there is expected to be a difference in performance between comparing two very human-like models
and comparing two very not human-like models.
In the last part of the simulation, we wished to explore
the sensitivity of our approach to the number of handshakes in each experiment. We repeated the analysis of
the Pure Turing-like test for different number of blocks,
10, 20, 40, 60, 80, 100, and 200.
Results
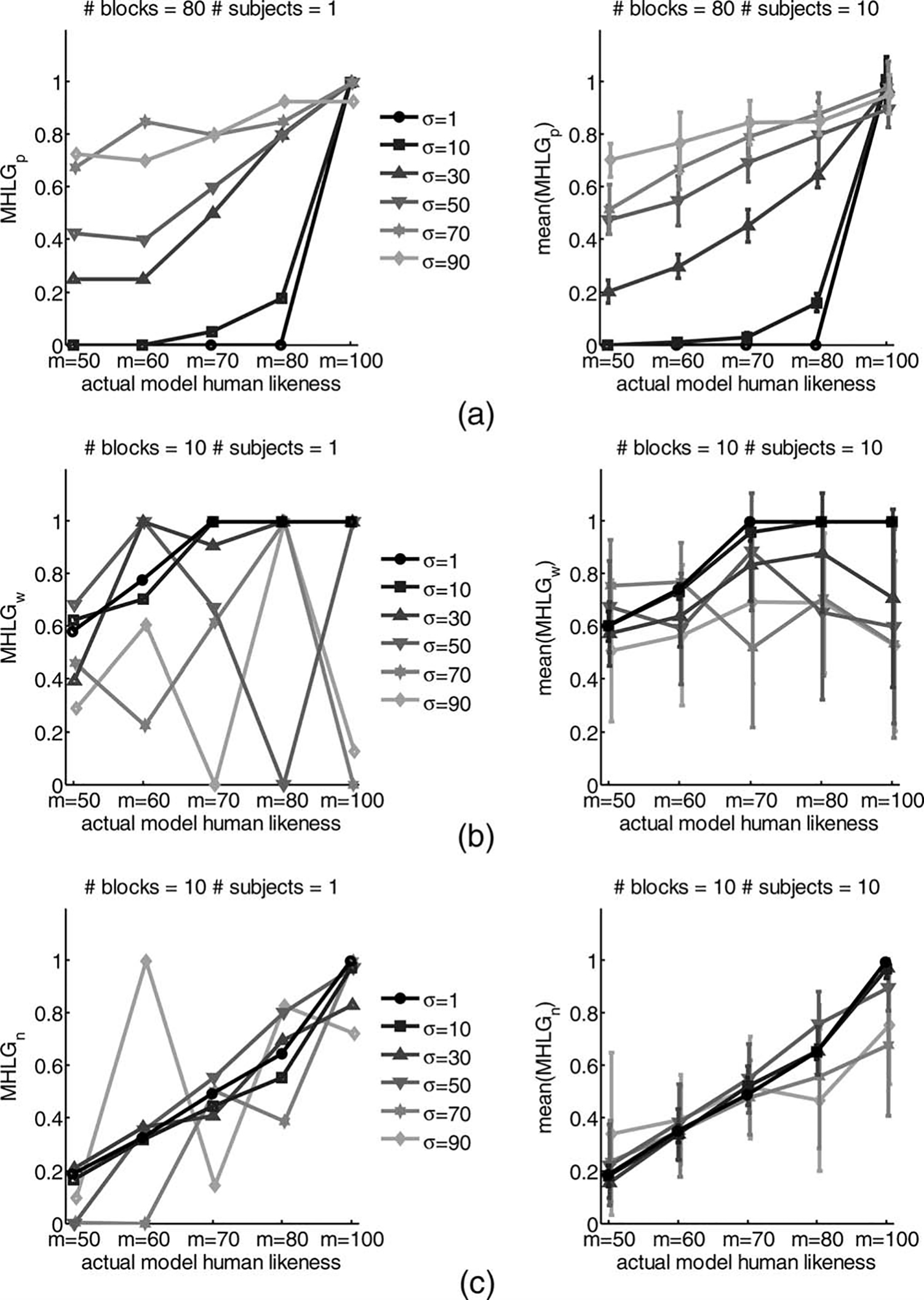
The results of the simulations of all three tests are
depicted in Figure 4. In the left panels of the figure, the results of one repetition of the simulation, and in the
right panels the mean of 10 MHLG from repetitions of
the simulation are presented together with 95 percent confidence intervals of the estimation of mean. Successful discrimination between the different models yields a statistically significant increase of the MHLG as the actual
model human-likeness increases. The results suggest that
the Pure Turing-like test is successful for intermediate
and large levels of decision variance of the interrogator,
and completely useless for low levels of variance. This is
not the case for the Weighted and Noise tests, which are
best for a low level of variance in the decision, and
become less sensitive with increasing decision variance.
Examining the right panels of Figure 4 leads to the
prediction that increasing the number of subjects is
expected to increase the sensitivity of almost all tests,
with the exception of the Pure test at the lowest levels of
decision variance.
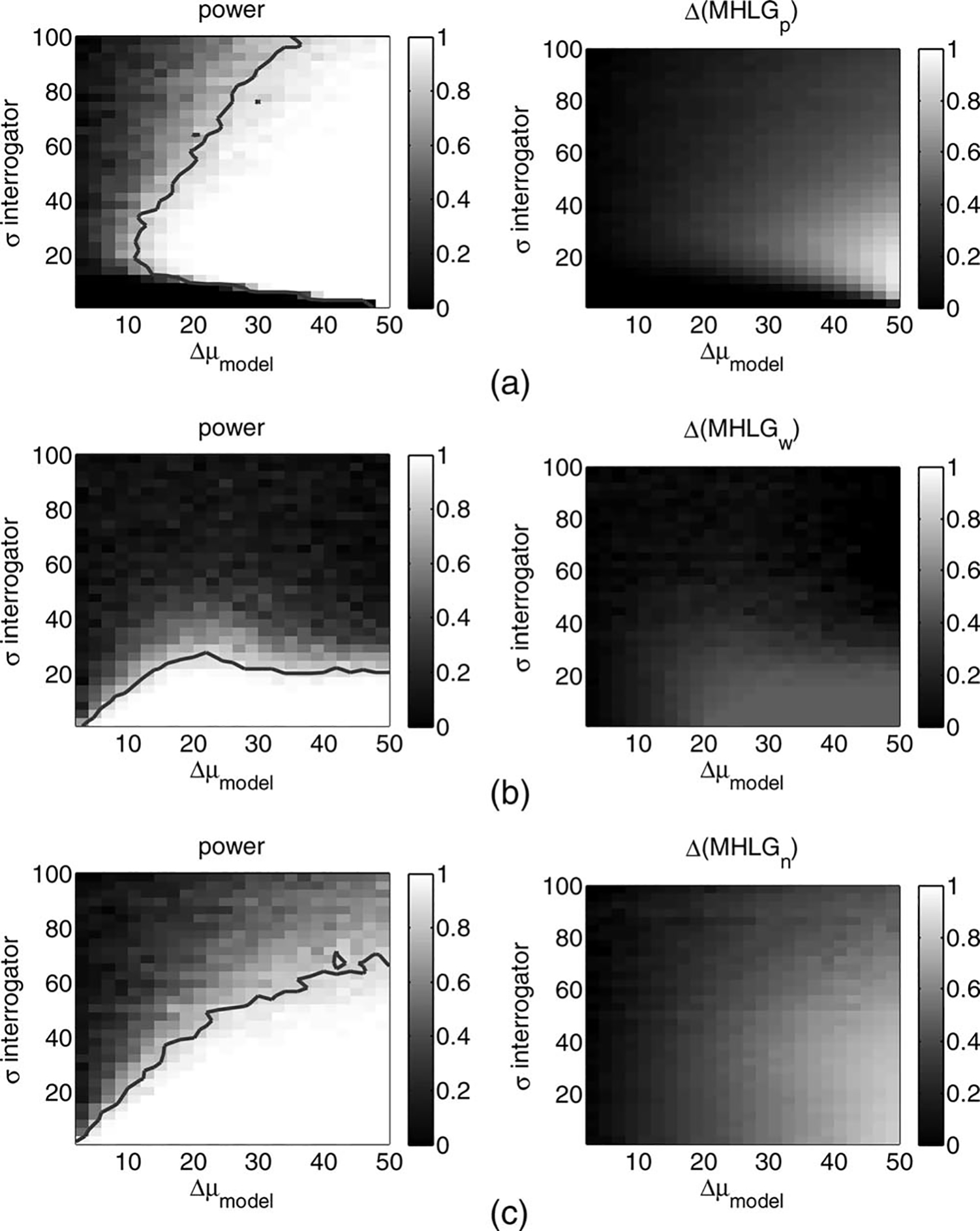
Statistical Power Analysis for
Comparison Between the Turing-Like Tests
The
results of the power and size of effect analysis for comparison between the least human-like model and all
other models are depicted in Figures 5 and 6, and support the qualitative observations from the previous paragraph. The results of power analysis for comparisons of
similar models (Δμ = 6) for models with different levels
of human-likeness are depicted in Figure 7.
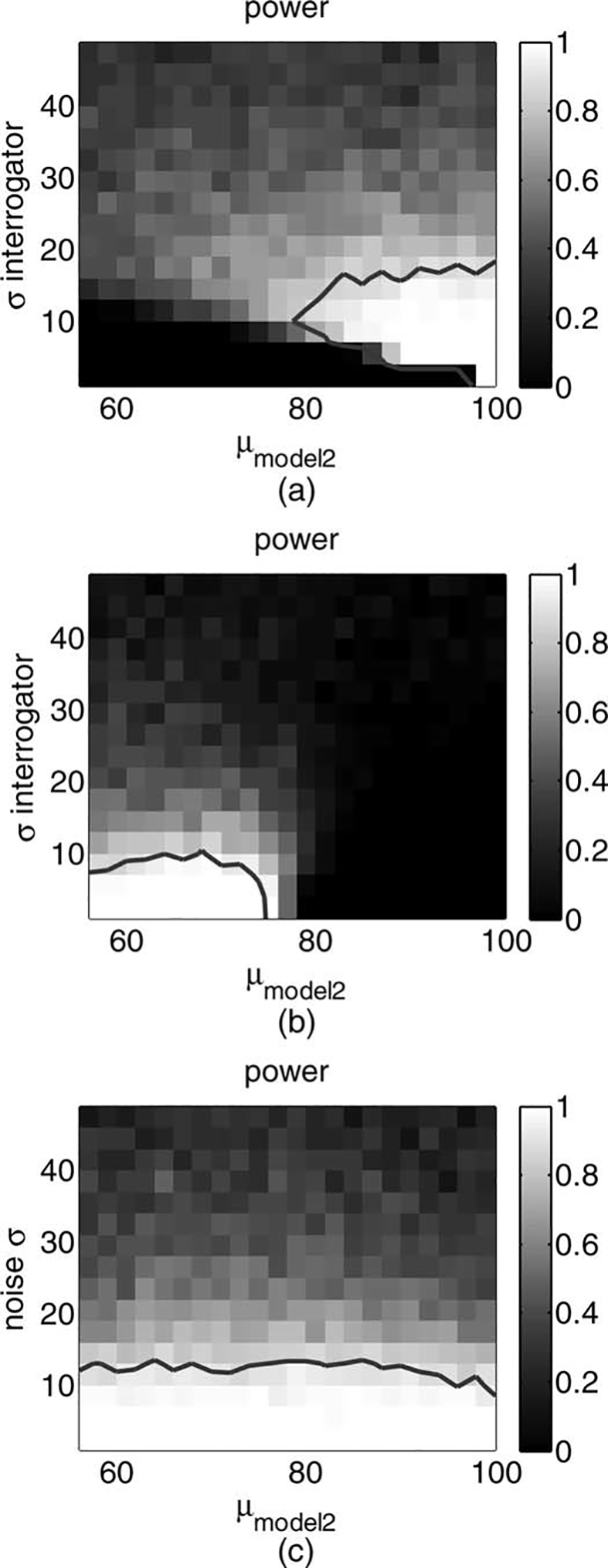
The Pure test has zero power for very small decision
variance, as shown in Figure 5(a) left. This is due to the
lack of overlap between the distributions of the internal
representations of human-likeness when the decision
variance is small. As the confusion of the interrogator
starts to increase, the power increases for large differences in human-likeness. The test is best for intermediate
levels of decision variance, σ ≈ 20; for these and larger
values, the Pure test has sufficiently high power starting
from Δμ > σ/3 (see Figure 6). Importantly, examining
the right part of Figure 5(a) suggests that the difference
in MHLGp values is a monotonically increasing function
of the difference between the hidden human-likeness
levels of each model. In an analysis of comparison
between similar models, Figure 7(a) reveals that the Pure
test is sensitive to difference between similar very human-like models (μ > 80) when the decision variance
is intermediate, namely 5 < σ < 20. In general, these
observations are in accordance with the following intuitive reasoning: When comparing two models to each
other, the Pure Turing-like test is effective if at least one
of the models is human-like enough such that there is
some overlap between the distribution of internal representation of human-likeness, and the interrogator will
make enough mistakes when asked to compare between
the human and computer handshakes. However, if both
models are very human-like, it will be difficult to distinguish between them when the decision variance is large.
The Weighted test has high statistical power for the
smallest level of interrogator decision variance, as shown
in the left part of Figure 5(b), and in Figure 6. As the decision variance increases, the test loses statistical power,
until it becomes not sensitive enough (power < 0.8) for
σ > 25. Examining the size of effect analysis, as shown
in the right side of Figure 5(b), reveals that this happens
since the difference in the mean value of MHLG
decreases. In addition, the difference in MHLGw values
is a monotonically increasing function of the difference
between the hidden human-likeness levels of each model
only in the range of interrogator decision variances
where the statistical power is high. This indicates a
potential caveat in the use of the Weighted test; however, since this only happens when the statistical power is
very low, it does not impose actual limitations. Namely, the Weighted test will not be used in this case, both
because of the lack of statistical power and because of inaccuracy. In an analysis of the comparison between similar
models, Figure 7(b) reveals that the Weighted test is sensitive to difference between similar models that are not very
human-like (μ < 75) for very low levels of decision variance σ < 10. These results are in accordance with the following intuitive reasoning: If both compared models are
more human-like than the reference model handshake
combined with the human handshake, they are both estimated as maximally human (MHLG = 1), and, therefore,
there is no statistically significant difference between them.
The Noise test, similar to the Weighted test, has high
statistical power for the smallest level of interrogator decision variance, as shown in the left part of Figure 5(c).
As the confusion level increases, the power is still high
for Δμ > σ/2, as shown in Figure 6. Examining the right
panel of Figure 5(c) reveals that similarly to the Pure
test, the difference in MHLGn values is a monotonically
increasing function of the difference between the hidden
human-likeness levels of each model. In addition, up to
σ = 40, this function does not change with interrogator
confusion level, which suggests more consistent results
between interrogators with different confusion levels. In
an analysis of the comparison between similar models, Figure 7(c) reveals that the Noise test is sensitive to a difference between similar models regardless of their level
of human-likeness for low levels of interrogator decision
variance, namely σ < 15.
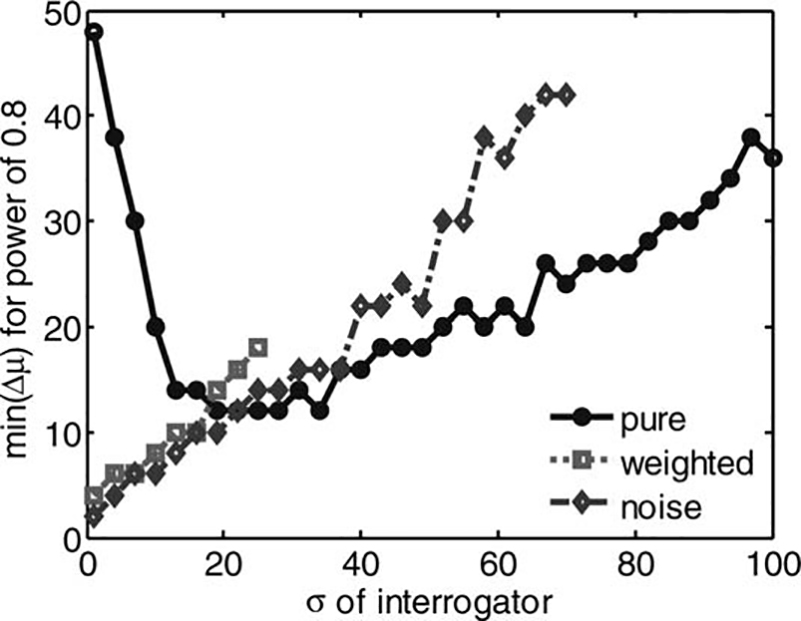
(b) Weighted, and (c) Noise Turing-like tests for human-likeness. The analysis is similar to the one that is described in Figure 5, but here the comparison was performed between each adjacent model, such that Δμ = 6. The abscissa is the human-likeness of the more human-like model, and the ordinate is the standard deviation of human-likeness. The contour is at the 0.8 level of statistical power.
To summarize, for very low levels of decision variance it
is appropriate to use either the Weighted or Noise
Turing-like tests. Starting from σ = 20, the Pure test outperforms the other tests. For very similar models, when
the decision variance is low, the Noise test is appropriate
for all levels of human-likeness, and the Weighted test is
appropriate only for not very human-like models. For intermediate levels of decision variance, the Pure tests
should be used, but it is likely to distinguish only between
similar very human like-models. For large levels of decision variance, none of the tests has enough statistical
power to be able to make statements about the difference
in human-likeness between very similar models.
The Effect of Number of Handshakes in
an Experiment
The power of any statistical analysis
increases with increasing sample size. This happens since
the uncertainty in any estimation is reduced when more
data are sampled. Our MHLG estimation is not an exception to this rule. Indeed, analysis of the power of the
Pure test, as shown in Figure 8, reveals that using more handshakes in the assessment of MHLG yields smaller
confidence intervals for the estimated MHLG, as shown
in Figure 8(a), and an increase in the statistical power, as
shown in Figures 8(b) and 8(c). The increase in the
power is due to the decrease in estimation uncertainty
(not to be confused with the interrogator’s decision variance), and not in the size of the mean difference in
MHLG, which is similar to the right panel of Figure 5(a)
regardless of number of blocks. Importantly, we conclude from Figure 8(c) that the increase of power is not
very high for more than 80 handshakes, and, therefore,
we chose 80 handshakes per model in our experimental
studies that are described in the next section.
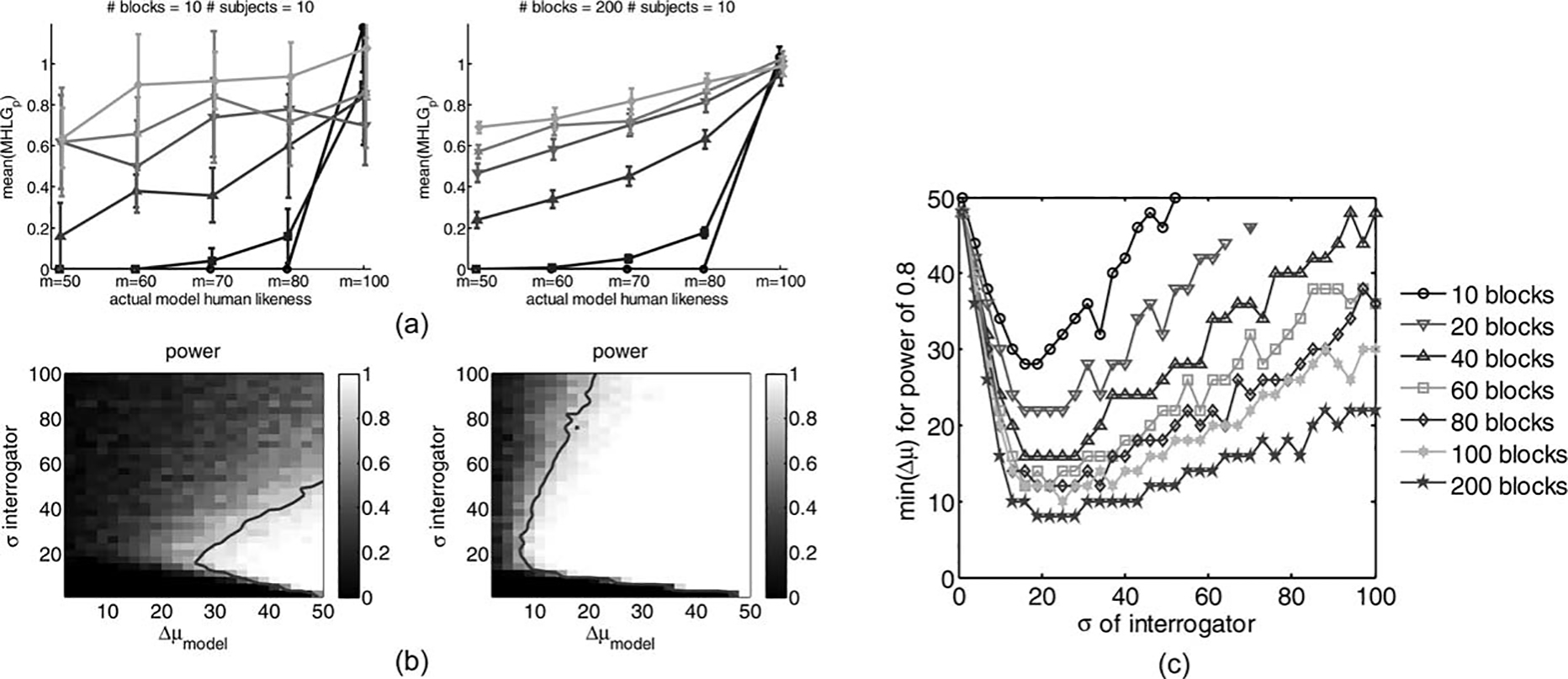
in Figure 5(a), but now for 10 (left) or 200 (right) blocks, instead of 80. (c) The minimal difference between models that yield power of 0.8 in a paired one-sided t-test for the Pure test with 10, 20, 40, 60, 80, 100, and 200 blocks.
Experiment
In the current section, we present our experimental
comparison of the three Turing-like tests while trying to
assess the human-likeness of three simple models for a
human handshake.
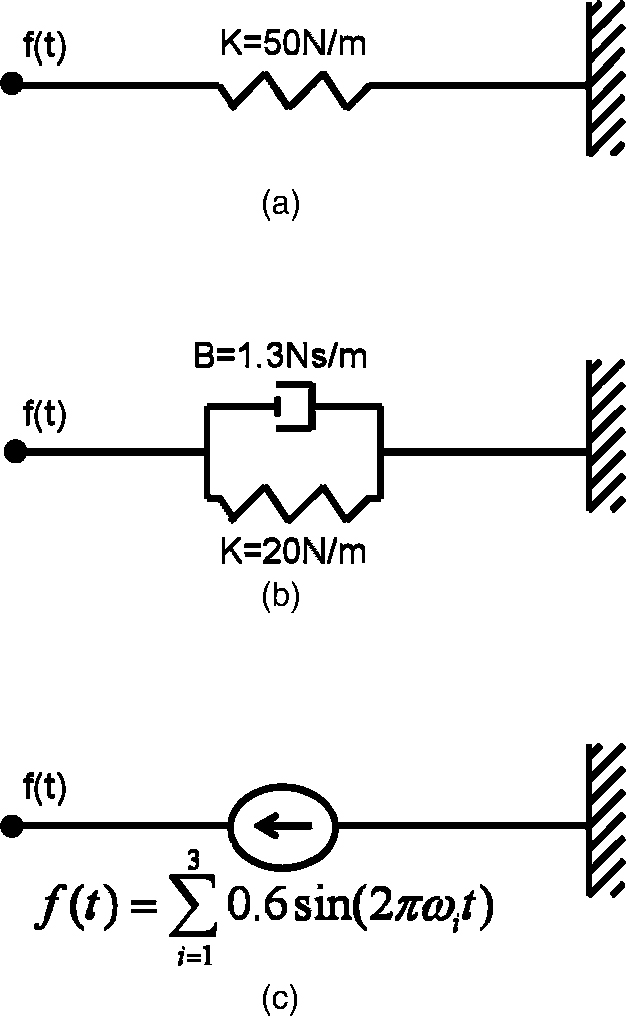
Models for Human Handshake
A computer model of a human handshake is a force
signal as a function of time, 1D position of the interroga-
tor’s hand, xinter(t), and its derivatives. In the most general notation, such a function is presented in Equation 3.
In our experimental study, we compared three simple
versions of such a function, which are depicted schematically in Figure 9. We considered three candidate models,
the linear spring, the linear spring and damper, and the
mixture of sinusoids.
1. Linear spring, K = 50 N/m, namely:
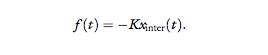
This model was chosen because it describes a very
simple function between the movement of the
interrogator and the force applied by the model
that creates a form of interaction.
2. Linear spring and damper connected in parallel,
K = 20 N/m, B = 1.3 Ns/m, namely:
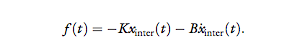
This model was chosen to represent the passive
mechanical characteristics of human movement.
It has an additional parameter when compared
with the previous model, and therefore, it is
expected to be ranked higher on the MHLG
scale.
3. Mixture of sinusoids with frequencies within the
typical range of human movement, between 1.5
and 2.5 Hz (Avraham et al., 2009, 2010; Karniel,
2010; Karniel, Nisky et al., 2010), namely:
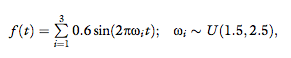
where U(a, b) is a uniform distribution between a and b, with the probability density function
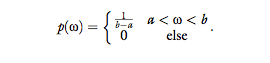
This model was chosen to represent the class of
active handshakes, where the force applied on the
interrogator is actually not a function of his or
her movements.
Methods
Experimental Procedure, Apparatus,
and Architecture
Thirty volunteers participated in the
experiments after signing the informed consent form as
stipulated by the local Helsinki Committee. In each
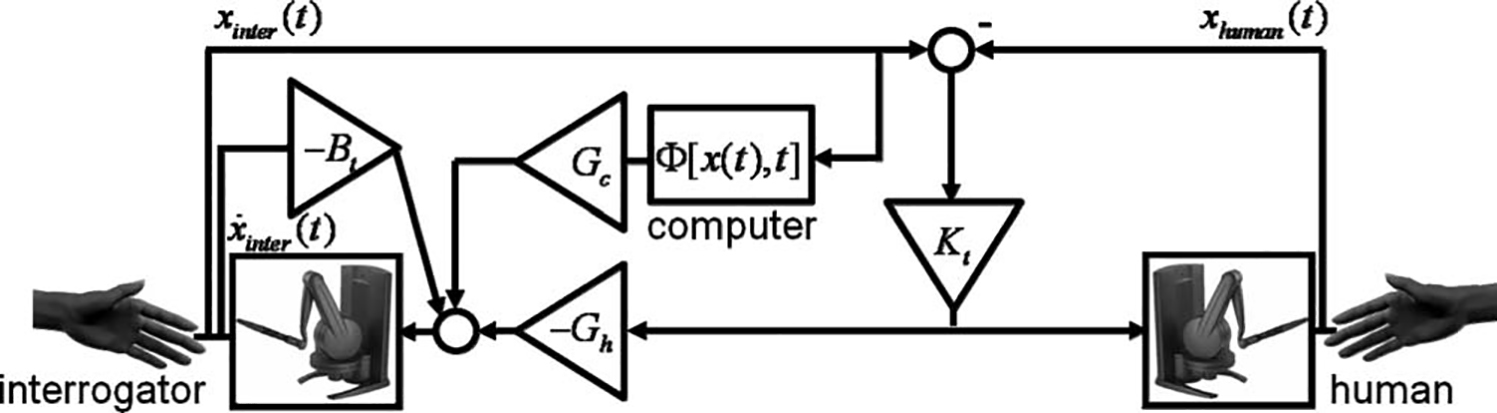
experiment, two naive participants—human and interrogator—held the stylus of a PHANToM Desktop haptic device (SensAble Technologies) and generated handshake movements, as depicted in Figure 1. Throughout
the experiment, the interrogator was requested to answer which of the two handshakes within a single trial
felt more human by pressing the appropriate key on the
keyboard. Both haptic devices were connected to a Dell
precision 450 computer with dual CPU, Intel Xeon 2.4
GHz processor. The position of the interrogator,
xinter(t), and of the human, xhuman(t), along the vertical
direction, were recorded at a sampling rate of 600 Hz.
These position signals were used to calculate the forces
that were applied to each of the devices according to the
overall system architecture that is depicted in Figure 10.
These forces were interpolated online and applied at
1000 Hz. The human always felt force that is proportional to the difference between the positions of the
interrogator and the human himself, namely:
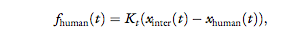
where Kt = 150N/m. The interrogator felt a force that
is a combination of this force, a computer-generated
function, and damping, namely:
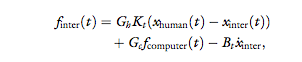
where Gh and Gc are the gains of the human and computer force functions, respectively, the computer generated force function fcomputer (t) is either a handshake
model or noise, Kt = 150 N/m is the gain of the position teleoperation channel, and Bt 1⁄4 2 Ns/m is damping
that is added at the interrogator side to ensure overall
system stability. The gains and the computer-generated
function were determined according to the exact protocols that are specified further.
The experiments were divided into two sessions that
were performed in two visits to the lab on different days.
Each session started with practice of 60 handshakes in
which the interrogator shook hands with the human
through the telerobotic system, namely Gh = 1 and Gc =
0. The purpose of these practice trials was to enable the
participants to be acquainted with a human handshake in
our system.
Experiment 1: Pure
Five pairs of volunteers participated in the experiment. Each experimental block consisted of three trials in
which we compared each of the three candidate models
to a human handshake. In each trial, the interrogator was
presented with a pure computer handshake, namely Gh =
0 and Gc = 1, and pure human handshake, namely Gh = 1
and Gc = 0. The computer-generated force function was
calculated according to one of the models, Equations 12,
13, or 14. Each block consisted of three trials such that
each model was presented once. The order of the trials
within each block was random and predetermined. Following our simulation, each experiment consisted of 80
test blocks. Two blocks were added at the beginning of
the experiment for general acquaintance with the system
and the task. The answers of the subjects in these blocks
were not analyzed. In order to preserve the memory of
the feeling of a human handshake in the telerobotic setup,
after each group of nine experimental blocks (27 trials),
the subject was presented with six human handshakes. To
increase the motivation of the participants, they received a
grade at the end of each block that was calculated based
on their answers in the block.
After completion of both sessions, we calculated
for each of the models the MHLGp according to
Equation 5.
Experiment 2: Weighted
Five pairs of volunteers participated in the experiment. In each trial the interrogator was presented with
two different combinations of a human handshake and a
model, a standard and a comparison handshake. The
force that was applied on the interrogator was calculated
according to Equation 15 with Gh = α and Gc = 1-α.
The values of α were α = αcomparison and α = αstandard for
the comparison and standard handshakes, respectively.
The model in the standard handshake was always the linear spring, Equation 12, and the model in the comparison handshake was one of our three candidate models,
Equations 12, 13, or 14.
Each experimental block consisted of 24 trials comprising each of the eight linear combinations of the stimulus and the human, Equation 6 with α = αcomparison, for each of the three models. The order of the trials within
each block was random and predetermined. Each experiment consisted of 10 blocks. Thus, each of the models
was presented to the interrogator in 80 comparison
handshakes. We added one practice block, namely 24 trials, for general acquaintance with the system and the
task. The answers of the interrogator in this block were
not analyzed. In order to preserve the memory of the
feeling of a human handshake in the telerobotic setup,
after each experimental block (24 trials), the subject was
presented with six human handshakes. To increase the
motivation of the participants, at the end of each block,
they received a grade that was calculated based on their
answers in the trials where the linear spring model was
presented both in comparison and standard handshakes.
In these trials, one of the handshakes is always composed
of a greater weight of human forces than the other handshake. We assume that a handshake with larger weight of
human versus computer handshake is perceived as more
human, and therefore, if the same model appears in both
handshakes with different weights, the participant should
be able identify the handshake that is more similar to
that of a human.
After completion of both sessions, we used the Psignifit toolbox version 2.5.6 for MATLAB to fit a logistic
psychometric function (Wichmann & Hill, 2001) to the
answers of the interrogator and extract the PSE. We then
calculated the MHLGw of each of the models according
to Equation 7.
Experiment 3: Noise
Five pairs of volunteers participated in the experiment. In each trial, the interrogator was presented with a
pure computer handshake, namely Gh = 0 and Gc = 1,
which was one of the three candidate models, Equations
12, 13, or 14, and a human handshake combined with
noise, namely Gh =1 – β and Gc = β. The values of β
were determined according to Equation 8. The noise
function was calculated according to:
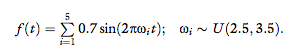
Note that the model for noise is similar to our mixture
of sinusoids model, but the random frequencies were chosen above the typical bandwidth for human movements, between 2.5 and 3.5 Hz (Avraham et al., 2009,
2010; Karniel, 2010; Karniel, Nisky et al., 2010). In
addition, we used a mixture of five rather than three sinusoids to ensure that the resultant signal would be perceived as noise by human subjects. We chose the amplitude of the sinusoids in the noise function such that the
power of the noise signal was at least as high as the
power that is generated during interaction with the
tested models in the Pure test.
Within each block, there were eight trials in which the
combined human-noise handshake with Gh =1 – β and
Gc 1= β for each of the eight values of β was compared to a
combined human-noise handshake with Gh = 0.5 and Gc
= 0.5. These trials were added to serve as data for a calibration curve for each subject, to make sure that, indeed,
the human handshake with the higher noise component is
perceived as less human-like. Overall, each experimental
block consisted of 32 trials in which each of the eight linear combinations of the noise and the human (Equation
8) were compared with each of the three models and the
noise combined with the human model. Each experiment
consisted of 10 blocks. Thus, each of the models was presented to the interrogator in 80 handshakes, similar to the
protocols in Experiments 1 and 2. One experimental block
(32 trials) was added at the beginning of the experiment
for general acquaintance with the system and the task. The answers of the subjects in this block were not analyzed. In
order to preserve the memory of the feeling of a human
handshake in the telerobotic setup, after each experimental
block, the subject was presented with six human handshakes. To increase the motivation of the participants, at
the end of each block, they received a grade that was calculated based on their answers in the calibration trials.
After completion of both sessions, we fitted psychometric functions to the answers of the interrogators,
extracted the PSE, and calculated the MHLGn of each of
the models according to Equation 9.
Statistical Analysis
The values of MHLG
are bounded in [0,1], regardless of the specific version of
the Turing-like test that is used. Therefore, we used the
nonparametric Friedman’s test (M. Friedman, 1937) in
order to determine whether the difference between the
MHLG values of the models is statistically significant.
We used the Wilcoxon sign-rank test with Bonferroni
correction for multiple comparisons in order to perform
the comparisons between the individual models.
Results
Examples of psychometric curves that were fitted
to the answers of two selected interrogators from the
Weighted and Noise tests are depicted in Figure 11.
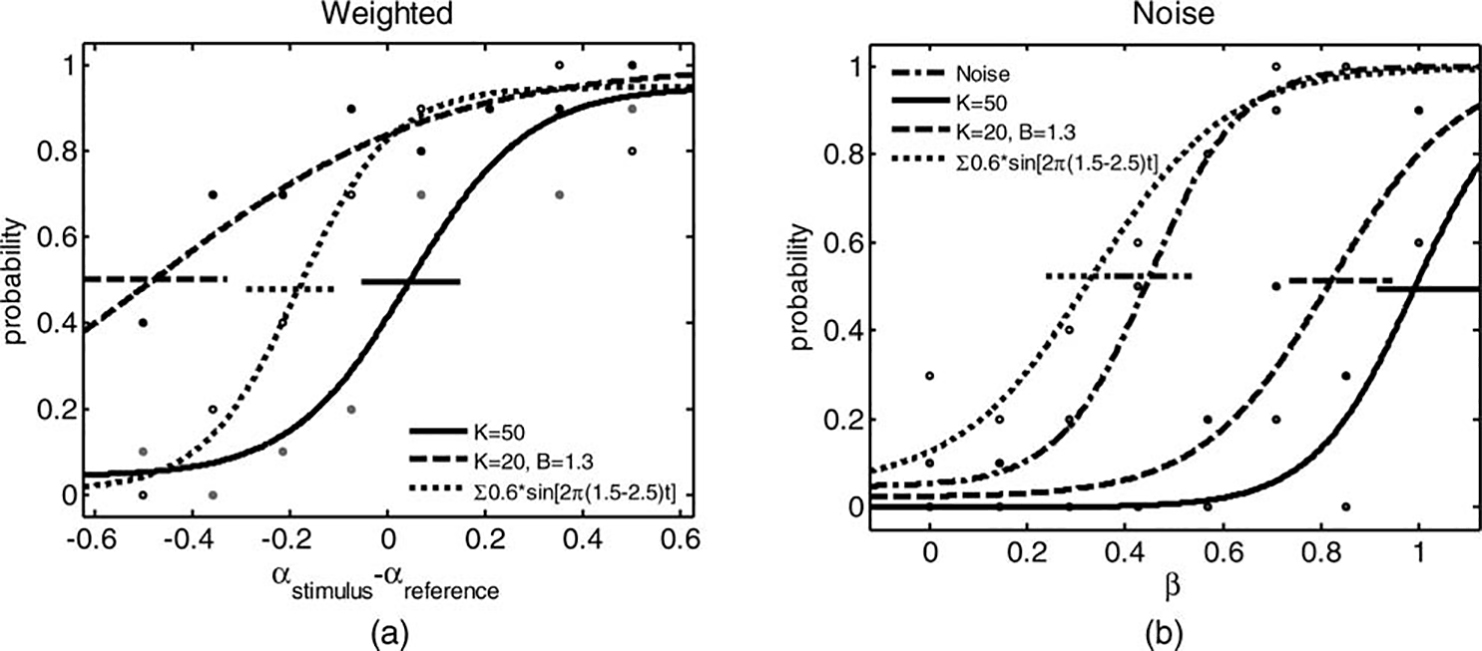
First, as evident from the successful fitting of psychometric curves, we validated the assumptions that a handshake
with higher weight of human handshake relative to a computer generated model for handshake or noise has
higher probability to be chosen as more human-like.
Moreover, the calibration curves (i.e., the spring model
in panel A and the noise model in panel B) indeed yield
PSE that is not statistically significantly different from 0
and 0.5, respectively.
Both interrogators perceived the linear spring model
as the least human-like (solid curves). However, the
spring and damper model was identified as most human-like in the Weighted test (Panel A, dashed curve), while
the mixture of sinusoids model was perceived as the most
human-like in the Noise test (Panel B, dotted curve).
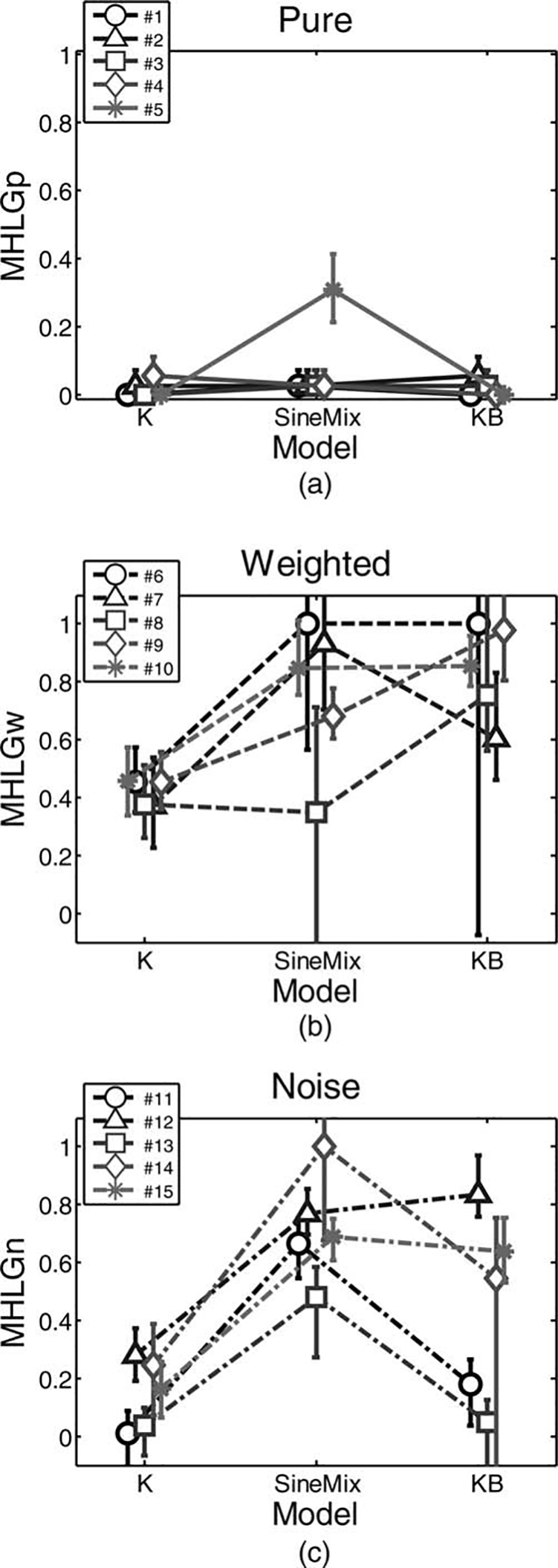
The MHLG of individual subjects for each of the
Turing-like tests are presented in Figure 12. Estimations
of the mean of MHLG of all models from all tests are
presented in Figure 13, together with the 95 percent confidence intervals for these estimations. The Pure test was
not sensitive enough for discriminating between the
MHLG values of the three tested models, as shown in
Figure 12(a), and there was no statistically significant
effect of model (Friedman’s test, p = .45). This was due
to the fact that when each of the interrogators was introduced with one of the models and with a human handshake, he or she almost always correctly identified the
human handshake, yielding very small MHLG values.
This suggests that all three models of handshake were far
from being a human-like handshake relative to the level
of confusion of the interrogator, similar to the simulated
results for very low decision variance (σ < 20).
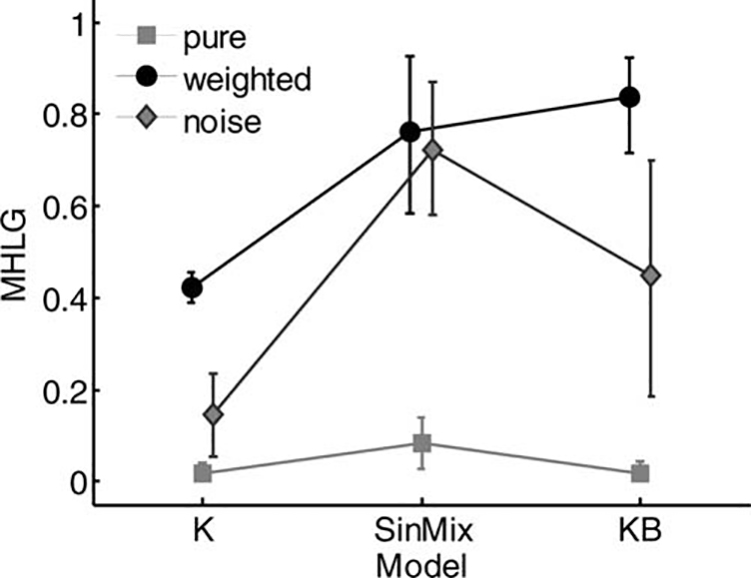
Consistent with the predictions from our simulation
study, the Weighted and Noise tests revealed a significant effect of model on MHLG (Friedman’s test, p =
.049 and p = .015, respectively), as is clearly evident in
Figure 12(b–c) and Figure 13. This leads to the conclusion that for these models, the more appropriate test is
either the Weighted or Noise Turing-like test. Interestingly, while the linear spring model was least human-like
according to both tests, there was no agreement about
the most human-like model: the mixture of sinusoids
model was the most human-like according to the
Weighted test, and the linear spring and damper model
was the most human-like according to the Noise test.
Discussion
In this study, we considered three versions of a
Turing-like handshake test: Pure, Weighted, and Noise.
In all these tests, a human interrogator interacts with different combinations of pairs of human, computer, or
combined handshakes, and is asked which handshake felt
more human. We presented a simulation study that
quantified the differences between these tests in their
ability to assess the human-likeness of computer-generated handshakes. We concluded the paper with an
experimental demonstration of testing the human-likeness of three simple models for the human handshake.
The simulation study suggests that the choice of the
best test to differentiate the human-likeness of computer-generated handshakes depends on how well the
interrogator identifies a human handshake when compared with a model, namely, the decision variance of the
interrogator. The Pure test is better for intermediate and
large levels of interrogator confusion, and the Weighted
and Noise tests are good for low levels of confusion.
While it seems that the Noise test outperforms the
Weighted test, an important condition must be satisfied
before an effective Noise test can be implemented: we
have to define the noise function—the least human-like
handshake possible. Therefore, the Weighted test is necessary at least for finding a model that is far enough from
a human handshake to serve as noise.
In our simulation study, we assumed that the 1D
internal-representations of a handshake human-likeness has a Gaussian distribution, and that for all computer,
human, and combined handshakes, and for all subjects,
this distribution has an identical standard deviation.
These assumptions are probably not correct; for example, the assumption of constant variance does not take
into account the Weber and Fechner laws (Norwich,
1987). We did not take into account the possibility that
the decision process concerning the level of human-likeness of a handshake has a multiplicative rather than additive noise, and a particular structure of observer model
(Lu & Dosher, 2008). In order to properly take these
properties into account in our assumptions, we would
have to choose the observer model (Lu & Dosher), the
appropriate power function that relates the actual level
of stimulus to the perceived human-likeness, and even
decide whether such a function exists (Stevens, 1957).
Since there is no established characterization of the perception of handshake psychophysics, we chose to start
with the simplest assumptions. With future progress in
the psychophysical evaluation of human-likeness of computer-generated handshakes, these assumptions would
probably be revised and additional methodological progress would be possible based on more true-to-life
formulations.
According to our experimental results, the Pure test
was not successful in discrimination of human-likeness of
the linear spring, linear spring and damper, and mixture
of sinusoids models for human handshake. This implies
that the decision variance of the interrogator is low, and
that the suggested models are far from being human-like. Therefore, when the interrogator is asked to compare a human handshake and a model handshake, he or
she mostly chooses the correct answer. However, consistent with our simulations, both the Weighted and
Noise test successfully discriminated between these simple models. We expect that when we will test models for
handshake that are more human-like, the Pure test will
become more effective for discriminating between them
and for identifying the most human-like handshake
model. This observation suggests an additional methodological recommendation: for each new set of models,
it is useful to perform a pilot study with a small number
of subjects but using all three Turing-like tests. The
results of these tests taken together can be used as an operational estimation of the level of confusion of the
interrogator with respect to the human-likeness of the
tested models. For example, models that yield a consistent estimation of MHLGp = 0, MHLGw = 1, and 0 <
MHLGn < 1 indicate a low level of interrogator confusion, and a high level of human-likeness.
Interestingly, while in our simulation study, the grading of different models was consistent between Weighted
and Noise tests, this was not the case in the experimental
study. The linear spring model was consistently perceived as the least human-like model, but there was a disagreement about the human-likeness of the linear spring
and damper and mixture of sinuses models. One possible
explanation for this observation is that the internal representation of human-likeness is multidimensional. Each
interrogator might follow a different decision path in the
space of human-likeness features when grading the
models. An example of such a situation is when the
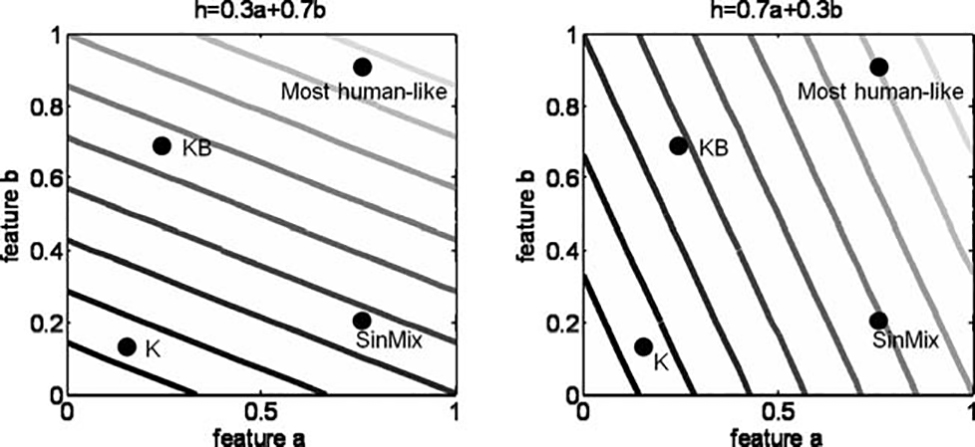
human-likeness is determined according to a weighted
average of the different features, as depicted in Figure
14. According to this view, all the interrogators would
correctly identify the least and the most human-like possible handshakes, but may have various opinions about
the salient feature characterizing human-likeness.
In particular, the linear spring and damper and mixture of sinusoids represent two different classes of models, a passive linear system, and an active stochastic force
generator, respectively. A priori, it is difficult to predict
which class is expected to be more human-like. A passive,
linear system creates forces only in response to the movement of the interrogator, and the frequency content of
the resultant handshake never contains frequencies that
did not exist in this movement. Hence, the resultant
handshake is highly synchronized, but also very predictive. Such a handshake would feel natural to an interrogator who is used to dominating handshakes, and who
always takes the leader role in a handshake. An active stochastic force generator introduces unpredicted frequency
content, and initiates interaction even if the interrogator
does not do so. Thus, such a handshake might feel more
human-like to an interrogator who is used to following
and complying with the other opponent’s movement
during everyday handshakes. However, it might feel out
of sync and unpleasant if the interrogator tries to lead
the handshake. These two features could be examples for
different dimensions of the overall human-likeness representation that were suggested in the previous paragraph,
and the weighting between these features could be
determined by the dominance of the interrogator in
physical interactions (Groten et al., 2009). In future
studies, these two features could be combined into one
model of a handshake. In addition, it might be beneficial
to identify the dominance of the interrogator in collaborative tasks in order to adjust the specific weight of active
and passive components in the handshake.
To further improve future models of handshake, it
can be useful to include a few theories about the nature
of the control of human movements. For example, the
linear spring and damper system can be replaced with a
Hill-type mechanical model (Karniel & Inbar, 1997) or
one-fifth power damping (Barto, Fagg, Sitkoff, & Houk,
1999). For the class of active models, it can be interesting to consider using trajectories that are the result of
optimization with respect to some cost function, for
example, minimum jerk (Flash & Hogan, 1985), or minimum acceleration with constraints (Ben-Itzhak &
Karniel, 2007), instead of the simple sinusoids that we
used in the current study. In addition, it is possible to incorporate forward models for controlling the grip
force (Flanagan & Wing, 1997; Kawato, 1999) into the
construction of control law, or to adopt optimal feedback control strategies (Todorov & Jordan, 2002) and
adaptive control. In Avraham et al. (in press), we
utilized the Noise Turing-like handshake test, and compared the human-likeness of three models that were
based on different aspects of the human control of
motion.
The difference in grading might be the result of the
subjective and declarative nature of the test. In order to
overcome the differences between the cognitive processes across subjects, it can be useful to look at objective,
physiologically related, measures, such as skin conductance response (Laine, Spitler, Mosher, & Gothard,
2009), heart rate (Anttonen & Surakka, 2005), postural
responses (Freeman, Avons, Meddis, Pearson, & IJsselsteijn, 2000), or task performance (Feth et al., 2011;
Schloerb, 1995). This is of special importance, as declarative perception is not always consistent with motor
responses (Aglioti, DeSouza, & Goodale, 1995; Ganel &
Goodale, 2003; Goodale & Milner, 1992; Nisky,
Pressman, Pugh, Mussa-Ivaldi, & Karniel, 2011; Pressman, Nisky, Karniel, & Mussa-Ivaldi, 2008). In particular, a declarative, subjective, evaluation of presence in virtual and remote environments was shown to be
unreliable, and behavioral, objective, presence measures,
such as postural responses, were suggested (Freeman et al.). In the context of human–robot interaction, Reed
and Peshkin (2008) showed that while participants who
interacted with a robotic partner reported that they
interacted with a human in the verbal Turing test, they
did not reach the same level of performance as in the
human–human dyad.
The use of virtual reality, telepresence, and teleoperation systems for the study of perception has been growing over the last few years (Jin, 2011; Zaal & Bootsma,
2011). In a recent work (Feth et al., 2011), human–robot interaction in a virtual environment was studied,
and the human-likeness of virtual partners with a predetermined or adaptive collaborative behavior was evaluated. They developed two psychophysical tests using a
predefined scale or a pair-wise comparison, to assess the
similarity of the virtual partner to a human partner in terms of haptic perception. Our Pure test resembles their
pair-wise comparison approach, but in our test, we compare each handshake model only to a human handshake,
while they applied Thurstone’s law of comparative judgment, Case V, and performed all possible paired comparisons between the different virtual opponents, as well as
random and human opponent. Both of these approaches
are based on Thurstonian scaling and SDT (MacMillan,
2002), but differ in the overall number of comparisons.
While our method is more economical in terms of experimental burden, as it uses a minimal number of comparisons, the method of Feth et al. provides a more direct
assessment of the relative human-likeness of each pair of
models, and, hence, provides a more accurate estimation.
In a future study, it will be interesting to compare these
two approaches in a single experiment with an identical
number of overall comparisons and assess the statistical
power of each of the methods in discrimination of
human-likeness.
There are two fundamentally different approaches to
the challenge of quantifying the perceived human-likeness of a particular model for the handshake. One is to
present the participants with various handshakes, and
ask for a quantitative grade on some predefined scale
(Feth et al., 2011; Ikeura et al., 1999). The other is to
use a 2AFC method: present the participant with two
handshakes and ask which one is more human-like (Feth
et al.; Karniel, Avraham, et al., 2010). The main advantage of the latter approach is that it allows us to treat the
problem within the well-studied signal detection theory
(Abdi, 2007b; Gescheider, 1985; Lu & Dosher, 2008;
MacMillan, 2002), and use the methodological tools
that were developed within this framework, for example,
fitting psychometric curves to the answers of participants, and assessing perception thresholds and discrimination sensitivity. The 2AFC method followed by fitting
of psychometric curves is used extensively in haptic exploration: the combination is used to assess perception
of height (Ernst & Banks, 2002), shape (Helbig &
Ernst, 2007), stiffness (Nisky, Baraduc, & Karniel,
2010; Nisky, Mussa-Ivaldi, & Karniel, 2008; Pressman
et al., 2008; Pressman, Welty, Karniel, & Mussa-Ivaldi,
2007), and more. The combination is also a very
prominent technique for exploring perception in other modalities such as auditory (Warren, Uppenkamp, Patterson, & Griffiths, 2003), visual (Hoffman, Girshick,
Akeley, & Banks, 2008), and smell (Uchida & Mainen,
2003). Importantly, the method is used not only for
pure sensory modalities discrimination assessment, but
also for quantifying cognitive representation, such as in
the case of perception of numerical information in monkeys (Nieder & Miller, 2004), the effect of linguistic
perception of motion verbs on perception of motion
(Meteyard, Bahrami, & Vigliocco, 2007), or recognition of emotions (Pollak, Messner, Kistler, & Cohn,
2009).
In the current study, we present three versions of the
Turing-like test for handshake. These tests complement
each other in their ability to discriminate between the
human-likeness of different computer models for different levels of confusion of the human interrogator. In our
experimental study, we focused on a reduced version of a
handshake: a 1D point interaction through a robotic
handle. This approach allows for an exploration of the
simple characteristics of human motion that contribute
to the perception of human-likeness. In the next step,
additional aspects of human-likeness should be explored,
both within and outside of the haptic modality, such as
grip force, texture, temperature, and moisture, as well as
vision and sound.
We believe that the current study provides an important step in the process of building human-like humanoid robots, and will help to facilitate development of natural human–robot interactions, with its promising
applications for teleoperation and telepresence.
Acknowledgments
This work was supported by the Israel Science Foundation
Grant number 1018/08. Ilana Nisky was supported by the
Kreitman and Clore foundations.
Lead photo by VCG/VCG via Getty Images
This article was originally published in the spring 2012 issue of the journal Presence.
References
Abdi, H. (2007a). The Bonferroni and Sidak corrections for
multiple comparisons. In N. Salkind (Ed.), Encyclopedia of
measurement and statistics. Thousand Oaks, CA: Sage.
Abdi, H. (2007b). Signal detection theory. In N. Salkind
(Ed.), Encyclopedia of measurement and statistics. Thousand
Oaks, CA: Sage.
Aglioti, S., DeSouza, J. F. X., & Goodale, M. A. (1995). Size-contrast illusions deceive the eye but not the hand. Current
Biology, 5(6), 679–685.
Anttonen, J., & Surakka, V. (2005). Emotions and heart rate
while sitting on a chair. Paper presented at the SIGCHI
Conference on Human Factors in Computing Systems,
Portland, Oregon.
Avraham, G., Levy-Tzedek, S., & Karniel, A. (2009). Exploring
the rhythmic nature of handshake movement and a Turing-like test. Paper presented at the Fifth Computational Motor
Control Workshop, Beer-Sheva, Israel.
Avraham, G., Levy-Tzedek, S., Peles, B.-C., Bar-Haim, S., &
Karniel, A. (2010). Reduced frequency variability in hand-
shake movements of individuals with cerebral palsy. Paper pre-
sented at the Sixth Computational Motor Control Work-
shop, Beer-Sheva, Israel.
Avraham, G., Nisky, I., Fernandes, H., Acuna, D., Kording,
K., Loeb, G., & Karniel, A. (submitted). Towards perceiving
robots as humans—Three handshake models face the
Turing-like handshake test. IEEE Transactions on Haptics.
doi:10.1109/TOH.2012.16.
Avraham, G., Nisky, I., & Karniel, A. (2011). When robots
become humans: A Turing-like handshake test. Paper presented at the CMCW7, Seventh Annual Computational
Motor Control Workshop at Ben-Gurion University of the
Negev, Beer-Sheva, Israel.
Bailenson, J. N., & Yee, N. (2008). Virtual interpersonal
touch: Haptic interaction and copresence in collaborative
virtual environments. Multimedia Tools and Applications,
37(1), 5–14. doi:10.1007/s11042-007-0171-2
Bailenson, J. N., & Yee, N. (2007). Virtual interpersonal touch
and digital chameleons. Journal of Nonverbal Behavior,
31(4), 225–242.
Bailenson, J. N., Yee, N., Brave, S., Merget, D., & Koslow, D.
(2007). Virtual interpersonal touch: Expressing and recog-
nizing emotions through haptic devices. Human–Computer
Interaction, 22(3), 325–353.
Barto, A. G., Fagg, A. H., Sitkoff, N., & Houk, J. C. (1999).
A cerebellar model of timing and prediction in the control of
reaching. Neural Computation, 11(3), 565–594.
doi:10.1162/089976699300016575
Ben-Itzhak, S., & Karniel, A. (2007). Minimum acceleration
criterion with constraints implies bang-bang control as an
underlying principle for optimal trajectories of arm reaching movements. Neural Computation, 20(3), 779–812.
doi:10.1162/neco.2007.12-05-077
Biggs, J., & Srinivasan, M. A. (2002). Haptic interfaces. In
K. Stanney (Ed.), Handbook of virtual environments
(pp. 93–115). Mahwah, NJ: Lawrence Erlbaum.
Chaplin, W. F., Phillips, J. B., Brown, J. D., Clanton, N. R., &
Stein, J. L. (2000). Handshaking, gender, personality, and
first impressions. Journal of Personality and Social Psychology,
79(1), 110–117.
Cohen, J. (1988). Statistical power analysis for behavioral sciences (2nd ed.). Mahwah, NJ: Lawrence Erlbaum.
Cohen, J. (1992). A power primer. Psychological Bulletin,
112(1), 155–159.
Durlach, N., & Slater, M. (2000). Presence in shared virtual
environments and virtual togetherness. Presence: Teleoperators and Virtual Environments, 9(2), 214–217.
doi:10.1162/105474600566736
El Saddik, A. (2007). The potential of haptics technologies. IEEE
Instrumentation & Measurement Magazine, 10(1), 10–17.
Ernst, M. O., & Banks, M. S. (2002). Humans integrate visual
and haptic information in a statistically optimal fashion.
Nature, 415(6870), 429–433.
Feth, D., Groten, R., Peer, A., & Buss, M. (2011). Haptic
human–robot collaboration: Comparison of robot partner
implementations in terms of human-likeness and task performance. Presence: Teleoperators and Virtual Environments,
20(2), 173–189. doi:10.1162/pres_a_00042
Flanagan, J. R., & Wing, A. M. (1997). The role of internal
models in motion planning and control: Evidence from grip
force adjustments during movements of hand-held loads.
The Journal of Neuroscience, 17(4), 1519–1528.
Flash, T., & Hogan, N. (1985). The coordination of arm
movements: An experimentally confirmed mathematical
model. Journal of Neuroscience, 5(7), 1688–1703.
Freeman, J., Avons, S. E., Meddis, R., Pearson, D. E., & IJsselsteijn, W. (2000). Using behavioral realism to estimate presence: A study of the utility of postural responses to motion
stimuli. Presence: Teleoperators and Virtual Environments,
9(2), 149–164. doi:10.1162/105474600566691
Friedman, M. (1937). The use of ranks to avoid the assump-
tion of normality implicit in the analysis of variance. Journal
of the American Statistical Association, 32(200), 675–701.
Friedman, R., Hester, K., Green, B., & LaMotte, R. (2008).
Magnitude estimation of softness. Experimental Brain
Research, 191(2), 133–142.
Ganel, T., & Goodale, M. A. (2003). Visual control of action
but not perception requires analytical processing of object
shape. Nature, 426(6967), 664–667.
Garcia-Perez, M. A., & Alcala-Quintana, R. (2011). Improving
the estimation of psychometric functions in 2AFC discrimi-
nation tasks. Frontiers in Psychology, 2(96), 1–9.
doi:10.3389/fpsyg.2011.00096
Gentry, S., Feron, E., & Murray-Smith, R. (2005). Human–human haptic collaboration in cyclical Fitts’ tasks. Paper presented at the IROS 2005, IEEE/RSJ International Conference on Intelligent Robots and Systems.
Gescheider, G. A. (1985). Method, theory, and application.
Mahwah, NJ: Lawrence Erlbaum.
Goodale, M. A., & Milner, A. D. (1992). Separate visual pathways for perception and action. Trends in Neurosciences,
15(1), 20–25.
Groten, R., Feth, D., Goshy, H., Peer, A., Kenny, D. A., &
Buss, M. (2009). Experimental analysis of dominance in hap-
tic collaboration. Paper presented at the RO-MAN 2009, the
18th IEEE International Symposium on Robot and Human
Interactive Communication.
Hannaford, B. (1989). Stability and performance tradeoffs in
bi-lateral telemanipulation. Paper presented at the ICRA
’89, IEEE International Conference on Robotics and Automation, Scottsdale, AZ.
Helbig, H., & Ernst, M. (2007). Optimal integration of shape
information from vision and touch. Experimental Brain
Research, 179(4), 595–606. doi:10.1007/s00221-006-
0814-y
Hespanha, J. P., McLaughlin, M., Sukhatme, G. S., Akbarian,
M., Garg, R., & Zhu, W. (2000). Haptic collaboration over
the internet. Paper presented at the Fifth PHANToM Users
Group Workshop.
Hinds, P. J., Roberts, T. L., & Jones, H. (2004). Whose job is
it anyway? A study of human–robot interaction in a collaborative task. Human–Computer Interaction, 19(1), 151–181.
doi:10.1207/s15327051hci1901&2_7
Hoffman, D. M., Girshick, A. R., Akeley, K., & Banks, M. S.
(2008). Vergence-accommodation conflicts hinder visual
performance and causes visual fatigue. Journal of Vision,
8(3). doi:10.1167/8.3.33
Ikeura, R., Inooka, H., & Mizutani, K. (1999). Subjective eval-
uation for maneuverability of a robot cooperating with
human. Paper presented at the RO-MAN 1999, 8th IEEE
International Workshop on Robot and Human Interaction.
Jin, S.-A. A. (2011). ‘‘It feels right. Therefore, I feel present
and enjoy’’: The effects of regulatory fit and the mediating roles of social presence and self-presence in avatar-based 3D
virtual environments. Presence: Teleoperators and Virtual
Environments, 20(2), 105–116.
Jindai, M., Watanabe, T., Shibata, S., & Yamamoto, T. (2006). Development of handshake robot system for embodied interaction with humans. Paper presented at the 15th IEEE International Symposium on Robot and Human Interactive Communication, Hatfield, UK.
Jones, L. A., & Hunter, I. W. (1990). A perceptual analysis of
stiffness. Experimental Brain Research, 79(1), 150–156.
Jones, L. A., & Hunter, I. W. (1993). A perceptual analysis of
viscosity. Experimental Brain Research, 94(2), 343–351.
Karniel, A. (2010). A Turing-like handshake test for motor intelligence. Paper presented at the 20th Annual Meeting of the
Society for Neural Control of Movement, Naples, Florida.
Karniel, A., Avraham, G., Peles, B.-C., Levy-Tzedek, S., & Nisky,
I. (2010). One dimensional Turing-like handshake test for
motor intelligence. Journal of Vision Exploration, 46, e2492.
Karniel, A., & Inbar, G. F. (1997). A model for learning
human reaching movements. Biological Cybernetics, 77(3),
173–183. doi:10.1007/s004220050378
Karniel, A., & Mussa-Ivaldi, F. A. (2003). Sequence, time, or
state representation: How does the motor control system
adapt to variable environments? Biological Cybernetics, 89(1),
10–21.
Karniel, A., Nisky, I., Avraham, G., Peles, B.-C., & Levy-
Tzedek, S. (2010). A Turing-like handshake test for motor
intelligence. In A. Kappers, J. van Erp, W. Bergmann Tiest, &
F. van der Helm (Eds.), Haptics: Generating and perceiving
tangible sensations (Vol. 6191, pp. 197–204). Berlin:
Springer.
Kasuga, T., & Hashimoto, M. (2005). Human-robot handshak-
ing using neural oscillators. Paper presented at the International Conference on Robotics and Automation, Barcelona,
Spain.
Kawato, M. (1999). Internal models for motor control and trajectory planning. Current Opinion in Neurobiology, 9(6),
718–727. doi:10.1016/s0959-4388(99)00028-8
Kim, J., Kim, H., Tay, B. K., Muniyandi, M., Srinivasan, M. A.,
Jordan, J., . . . Slater, M. (2004). Transatlantic touch: A
study of haptic collaboration over long distance. Presence:
Teleoperators and Virtual Environments, 13(3), 328–337.
doi:10.1162/1054746041422370
Kunii, Y., & Hashimoto, H. (1995). Tele-handshake using
HandShake device. Paper presented at the 1995 IEEE
IECON, 21st International Conference on Industrial Electronics, Control, and Instrumentation.
Laine, C. M., Spitler, K. M., Mosher, C. P., & Gothard, K. M.
(2009). Behavioral triggers of skin conductance responses
and their neural correlates in the primate amygdala. Journal
of Neurophysiology, 101(4), 1749–1754. doi:10.1152/
jn.91110.2008
Lu, Z.-L., & Dosher, B. A. (2008). Characterizing observers
using external noise and observer models: Assessing internal
representations with external noise. Psychological Review,
115(1), 44–82. doi:10.1037/0033-295x.115.1.44
MacMillan, N. A. (2002). Signal detection theory. Stevens’
handbook of experimental psychology. New York: John Wiley.
McLaughlin, M., Sukhatme, G., Wei, P., Weirong, Z., &
Parks, J. (2003). Performance and co-presence in heterogeneous haptic collaboration. Paper presented at the HAPTICS
2003, 11th Symposium on Haptic Interfaces for Virtual
Environments and Teleoperator Systems.
Meteyard, L., Bahrami, B., & Vigliocco, G. (2007). Motion
detection and motion verbs. Psychological Science, 18(11),
1007–1013. doi:10.1111/j.1467-9280.2007.02016.x
Miller, J., & Ulrich, R. (2001). On the analysis of psychometric
functions: The Spearman-Ka ̈rber method. Attention, Perception, & Psychophysics, 63(8), 1399–1420. doi:10.3758/
bf03194551
Miyashita, T., & Ishiguro, H. (2004). Human-like natural
behavior generation based on involuntary motions for
humanoid robots. Robotics and Autonomous Systems, 48(4),
203–212.
Morasso, P. (1981). Spatial control of arm movements. Experimental Brain Research, 42(2), 223–227.
Nieder, A., & Miller, E. K. (2004). Analog numerical representations in Rhesus monkeys: Evidence for parallel processing.
Journal of Cognitive Neuroscience, 16(5), 889–901.
doi:10.1162/089892904970807
Niemeyer, G., & Slotine, J.-J. E. (2004). Telemanipulation
with time delays. The International Journal of Robotics
Research, 23(9), 873–890. doi:10.1177/
0278364904045563
Nisky, I., Baraduc, P., & Karniel, A. (2010). Proximodistal gradient in the perception of delayed stiffness. Journal of Neurophysiology, 103(6), 3017–3026.
Nisky, I., Mussa-Ivaldi, F. A., & Karniel, A. (2008). A regression
and boundary-crossing-based model for the perception of
delayed stiffness. IEEE Transactions on Haptics, 1(2), 73–82.
Nisky, I., Pressman, A., Pugh, C. M., Mussa-Ivaldi, F. A., &
Karniel, A. (2011). Perception and action in teleoperated
needle insertion. IEEE Transactions on Haptics, 4(3),
155–166.
Norwich, K. (1987). On the theory of Weber fractions. Attention, Perception, & Psychophysics, 42(3), 286–298.
doi:10.3758/bf03203081
Okamura, A., Verner, L., Reiley, C., & Mahvash, M. (2011).
Haptics for robot-assisted minimally invasive surgery. In M.
Kaneko & Y. Nakamura (Eds.), Robotics research (Vol. 66,
pp. 361–372). Berlin: Springer.
Ouchi, K., & Hashimoto, S. (1997). Handshake telephone system to communicate with voice and force. Paper presented at
the IEEE International Workshop on Robot and Human
Communication.
Pollak, S. D., Messner, M., Kistler, D. J., & Cohn, J. F.
(2009). Development of perceptual expertise in emotion recognition. Cognition, 110(2), 242–247. doi:10.1016/
j.cognition.2008.10.010
Pressman, A., Nisky, I., Karniel, A., & Mussa-Ivaldi, F. A.
(2008). Probing virtual boundaries and the perception of
delayed stiffness. Advanced Robotics, 22, 119–140.
Pressman, A., Welty, L. J., Karniel, A., & Mussa-Ivaldi,
F. A. (2007). Perception of delayed stiffness. The
International Journal of Robotics Research, 26(11–12),
1191–1203.
Rahman, M. M., Ikeura, R., & Mizutani, K. (2002). Investiga-
tion of the impedance characteristic of human arm for devel-
opment of robots to cooperate with humans. International
Journal Series C Mechanical Systems, Machine Elements and
Manufacturing, 45(2), 510–518.
Reed, K. B., & Peshkin, M. A. (2008). Physical collaboration
of human–human and human–robot teams. IEEE Transactions on Haptics, 1(2), 108–120.
Roennqvist, L., & Roesblad, B. (2007). Kinematic analysis of
unimanual reaching and grasping movements in children
with hemiplegic cerebral palsy. Clinical Biomechanics, 22(2),
165–175.
Sato, T., Hashimoto, M., & Tsukahara, M. (2007). Synchronization based control using online design of dynamics and its
application to human–robot interaction. Paper presented at
the 2007 IEEE International Conference on Robotics and
Biomimetrics.
Schloerb, D. W. (1995). A quantitative measure of tele-
presence. Presence: Teleoperators and Virtual Environments,
4(1), 64–80.
Shadmehr, R., & Mussa-Ivaldi, F. A. (1994). Adaptive repre-
sentation of dynamics during learning of a motor task. Journal of Neuroscience, 14(5), 3208–3224.
Shadmehr, R., & Wise, S. P. (2005). The computational neurobiology of reaching and pointing: A foundation for motor
learning. Cambridge, MA: MIT Press.
Sheridan, T. B. (1994). Further musings on the psychophysics of
presence. Paper presented at the Humans, Information and
Technology, 1994 IEEE International Conference on Systems, Man, and Cybernetics.
Sheridan, T. B. (1996). Further musings on the psychophysics
of presence. Presence: Teleoperators and Virtual Environments, 5(2), 241–246.
Srinivasan, M. A., & LaMotte, R. H. (1995). Tactual discrimi-
nation of softness. Journal of Neurophysiology, 73(1),
88–101.
Stevens, S. S. (1957). On the psychophysical law. Psychological
Review, 64(3), 153–181. doi:10.1037/h0046162
Stewart, G. L., Dustin, S. L., Barrick, M. R., & Darnold, T. C.
(2008). Exploring the handshake in employment interviews.
Journal of Applied Psychology, 93(5), 1139–1146.
doi:10.1037/0021-9010.93.5.1139
Tan, H. Z., Durlach, N. I., Beauregard, G., & Srinivasan, M.
A. (1995). Manual discrimination of compliance using active
pinch grasp: The roles of force and work cues. Perception &
Psychophysics, 57(4), 495–510.
Todorov, E., & Jordan, M. I. (2002). Optimal feedback con-
trol as a theory of motor coordination. Nature Neuroscience,
5(11), 1226–1235. doi:10.1038/nn963
Turing, A. M. (1950). Computing machinery and intelligence. Mind, A Quarterly Review of Psychology and Philosophy, LIX(236).
Uchida, N., & Mainen, Z. F. (2003). Speed and accuracy of olfactory discrimination in the rat. Nature Neuroscience, 6(11), 1224–1229. doi:10.1038/nn1142
van Den, B. (2000). Coordination disorders in patients with Parkinson’s disease: A study of paced rhythmic forearm movements. Experimental Brain Research, 134(2), 174–186.
van der Heide, J. C., Fock, J. M., Otten, B., Stremmelaar, E., & Hadders-Algra, M. (2005). Kinematic characteristics of
reaching movements in preterm children with cerebral palsy.
Pediatric Research, 57(6), 883.
Wang, Z., Lu, J., Peer, A., & Buss, M. (2010). Influence of
vision and haptics on plausibility of social interaction in vir-
tual reality scenarios. In A. Kappers, J. van Erp, W. Berg-
mann Tiest, & F. van der Helm (Eds.), Haptics: Generating
and perceiving tangible sensations (Vol. 6192, pp. 172–177).
Berlin: Springer.
Wang, Z., Peer, A., & Buss, M. (2009). An HMM approach to
realistic haptic human–robot interaction. Paper presented at the World Haptics 2009, Third Joint EuroHaptics Conference, and Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems.
Warren, J. D., Uppenkamp, S., Patterson, R. D., & Griffiths,
T. D. (2003). Separating pitch chroma and pitch height in
the human brain. Proceedings of the National Academy of Sciences of the United States of America, 100(17), 10038–
10042. doi:10.1073/pnas.1730682100
Wichmann, F., & Hill, N. (2001). The psychometric function:
I. Fitting, sampling, and goodness of fit. Perception & Psychophysics, 63(8), 1293–1313.
Wolpert, D. M., & Ghahramani, Z. (2000). Computational
principles of movement neuroscience. Nature Neuroscience,
3, 1212–1217.
Yokokohji, Y., & Yoshikawa, T. (1994). Bilateral control of
master–slave manipulators for ideal kinesthetic coupling—
Formulation and experiment. IEEE Transactions on Robotics
and Automation, 10(5), 605–620.
Zaal, F. T. J. M., & Bootsma, R. J. (2011). Virtual reality as a
tool for the study of perception-action: The case of running
to catch fly balls. Presence: Teleoperators and Virtual Environments, 20(1), 93–103.

























