To say that Thomas Robert Malthus was unpopular would be putting it mildly. His 19th-century contemporary Percy Shelley, the revered poet, called him a eunuch and a tyrant. The philosopher William Godwin dubbed him “a dark and terrible genius that is ever at hand to blast all the hopes of all mankind.” As Malthus’ biographer later put it, he was the most abused man of his age. And that was the age of Napoleon Bonaparte.
The catalyst for this vilification was the 1798 book An Essay on the Principle of Population. In it, Malthus—a curly haired, 32-year-old curate of a small English chapel—attacked the claims of utopian thinkers like Godwin, who believed that reason and scientific progress would ultimately create a perfect society, free of inequality and suffering. Malthus took a more pessimistic view. Using United States census data compiled by Benjamin Franklin, he predicted that the “passion of the sexes” would soon cause human populations to outstrip their resources, leading to poverty and hardship. If unchecked, people would continue to multiply exponentially, doubling every 25 years. Agricultural yields, however, would at best increase linearly, by a similar amount each year. In 100 years, Great Britain would have 16 times as many mouths to feed (112 million), but less than half enough food.
That didn’t happen, of course. By 1900, the British population had swelled only fivefold, to 35 million citizens, most of them well fed. But Malthus foresaw the possibility of this slowdown in growth, too. To prevent populations from booming and busting—the infamous “Malthusian catastrophe”—he said that Nature imposed two types of checks. “Preventive” checks reduced the birth rate: When times were hard, and food scarce, men—particularly poor men—would foresee the troubles ahead and delay getting married and starting families. “Positive” checks—famine, disease, murder, war—increased the death rate. Once food production caught up with demand, however, strife would lessen and families would grow. Thus the “grinding law of necessity, misery, and the fear of misery” kept the size of a population oscillating in sync with supply. To his critics’ disgust, Malthus used this theory to argue against England’s Poor Laws, which provided welfare to needy families according to the number of children they had. Why encourage the poor to procreate, he argued, when Nature will turn around and trample them?

Malthus, though, had overlooked an important caveat. If Nature forces us to live within our means, Malthus drastically underestimated our ability to expand those means. By his death, in 1834, an agricultural revolution was underway in Europe. Farmers learned to breed plumper, faster-growing livestock and plant nitrogen-fixing crops to restore depleted soils. With the industrial revolution came coal-powered plows and threshers. And in the mid-1900s, the green revolution brought high-yielding seeds and synthetic fertilizers to growers worldwide. Between 1900 and 2000, in defiance of Malthus’ gloomy forecast, the global population quadrupled, from 1.6 to 6.1 billion. Meanwhile, grain production quintupled, from 400 million to 1.9 billion tons.
Regional famines aside, the human species has so far managed to avoid a Malthusian fate. Earth currently supports 7.3 billion people, and, according to the United Nations, that number will rise to 9.7 billion in 2050 and to 11.2 billion by the end of the century. If the planet has a maximum occupancy, it remains elusive. What Malthus failed to see was that the limit may depend as much on our own resourcefulness as on the laws of Nature.
While critics dismissed Malthus’ stark pessimism and cruel social politics, his ideas endured. Classical economists applied them in the defense of free-market capitalism. Both Charles Darwin and Alfred Russell Wallace cited Malthus’ book, with its emphasis on an inevitable struggle for existence, as inspiration for the theory of evolution by natural selection. But Malthus’ biggest influence was in the study of populations. His theory of natural checks launched the field of modern demography, and with it the quest to find humanity’s maximum growth, known as its carrying capacity.
In 1838, the Belgian mathematician Pierre Verhulst expanded on Malthus’ work by putting the theory in mathematical terms. Malthus had calculated unchecked growth by a simple formula: the size of a population, N, multiplied by the per capita increase, r (births minus deaths per person). Following this model, a population would keep growing and growing, faster and faster, forever. But Malthus had said that dwindling resources would eventually curb its growth. To account for this behavior, Verhulst added another factor to act as a brake, making the growth rate equal to
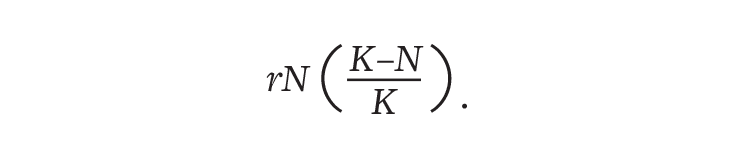
In this model, which Verhulst called the logistic function, K is the carrying capacity. At first, growth accelerates, as Malthus had assumed. But as N (population size) approaches K, growth slows to a crawl before stopping at its limit.
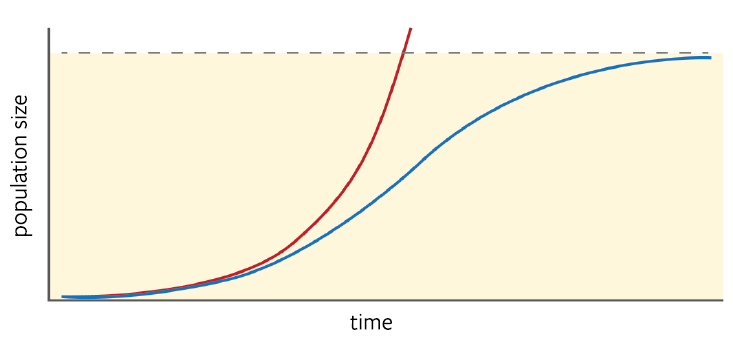
Fitting his new function to demographic trends in Belgium, Verhulst determined that the country’s population was growing at 2.6 percent per year, and would eventually max out at 6.6 million people. But he was wary of this prediction. Even though the curve nicely followed historical data, it relied on assumptions about the long-term nature of populations that might not be true. So two years later, he pushed the original function aside and had another go, producing the following revised description of the population growth rate:
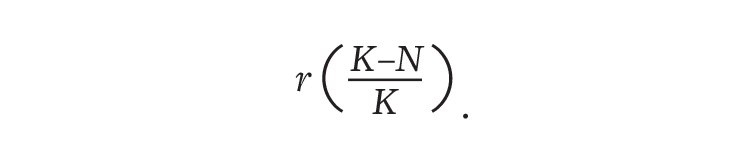
Like the logistic function, the adjusted model also matched past trends, but it resulted in a more gradual slowdown in growth as the population neared its limit. This bumped Belgium’s carrying capacity to 9.4 million. Neither estimate, however, turned out to be true. (The current tally is 11 million.) And Verhulst never came up with a solid mathematical theory he felt confident in. Even his former teacher and academic rival, Adolphe Quetelet, criticized his work for failing to provide a precise law for human behavior. After Verhulst died, in 1849, the logistic function faded into obscurity for more than 70 years.
Worries about population expansion resurfaced with World War I. “Population pressure is always a major cause of war,” remarked biologist Raymond Pearl in his 1925 book The Biology of Population Growth. As head statistician for the U.S. Food Administration during the conflict, Pearl had to keep an adequate supply of food flowing to troops, witnessing first-hand the economic struggles that Malthus had predicted. After the war, with statistician Lowell Reed, he developed a “logarithmic curve” to investigate how populations change.
Although the researchers didn’t know it at the time, they had stumbled upon Verhulst’s long-forgotten logistic function. When they fitted the curve to U.S. population data from 1790 to 1910, they found it was a remarkably good match. Their estimates of carrying capacity, however, weren’t any better than Verhulst’s. The U.S. limit, they said, would be about 200 million, which the population climbed past in 1968. (It is now at 319 million.) Pearl later estimated a world limit of 2 billion, which was surpassed by 1930.
Humans don’t just extract from a fixed set of resources, but can create new resources through invention.
The following decades saw the appearance of one carrying capacity estimate after another. In 1995, mathematician Joel Cohen, at Rockefeller University in New York, tallied up dozens of global forecasts published to date, and found that they varied widely, from less than 1 billion to more than 1 trillion. Most early estimates were, like Pearl’s, far below 6 billion, the world’s population at the time.
According to Cohen, their flaw lay in the assumption that resource constraints, and hence carrying capacity, were fixed. In mathematical lingo, K was a constant: It never changed. This presumption, Cohen said, ignored human innovation. “Let us recognize, in the phrase of U.S. president [George H.W. Bush], that ‘every human being represents hands to work, and not just another mouth to feed’,” he wrote in the journal Science. “Additional people clear rocks from fields, build irrigation canals, discover ore deposits and antibiotics, and invent steam engines; they also clear-cut primary forests, contribute to the erosion of topsoil, and manufacture chlorofluorocarbons and plutonium. Additional people may increase savings or dilute and deplete capital; they may increase or decrease the human carrying capacity.”
This had been the missing ingredient in early population models: Humans don’t just extract from a fixed set of resources, but can create new resources through invention.
In 1960, Heinz von Foerster and his colleagues at the University of Illinois were some of the first demographers to account for human ingenuity. They tweaked the logistic function to allow carrying capacity to vary with population size, resulting in the following formula for the growth rate:
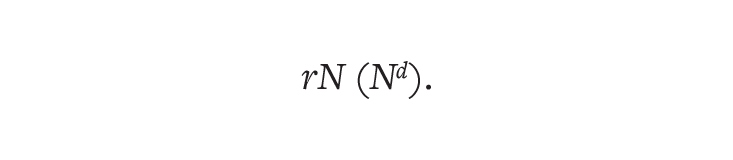
The constant d represents humanity’s impact on its resource pool. Based on historical patterns, the researchers concluded that d was equal to 1.01, meaning the pool was expanding. As the population grew, so did its ability to sustain itself, avoiding a Malthusian decline. Here was a way to quantify the power of innovation that previous models had missed.
Still, the future wasn’t exactly utopian. Solving their growth rate equation for population size N, the researchers concluded that in year t, N would be proportional to
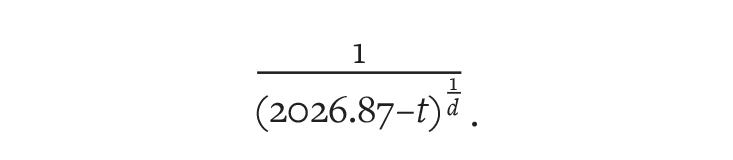
As time ticked forward, and t got closer and closer to 2026.87, the population would grow larger and larger. At this exact point, the bottom of the fraction would shrink to zero, causing population size to become infinite, or as mathematicians say, to “blow up.” Based on this analysis, the team predicted that Doomsday would come in 2026 A.D.
The precise date, which happened to fall in November, on Friday the 13th, was tongue-in-cheek. But Foerster’s observation that resources are a function of population size showed that innovation can change patterns of growth in ways that are hard to predict.

And technology doesn’t just affect the amount of resources that humans are able to extract; it also makes sharing those resources critically important. Take, for example, the question of space. Pearl’s calculations in the 1920s had suggested that about 4,000 people would eventually have to squeeze into every square mile of the U.S.—a density he said was “manifestly ridiculous.” Yet many cities already exceed this number, thanks to innovations such as high-rise architecture and indoor plumbing. The world’s most crowded places, including Mumbai and Seoul, now hold more than 40,000 people per square mile. But they still depend on provincial land to draw water, grow food, and generate power. A steady flow of goods between cities and the countryside can increase the carrying capacity of both. On the other hand, if one or the other is prevented from obtaining the resources it needs, both may suffer.
Countries, too, are interdependent: They trade with other nations and share global resources such as oceans, biodiversity, and climate. Understanding how a given nation will grow requires examining what happens outside its borders. In 2013, for instance, researchers led by Samir Suweis, at the University of Padua, in Italy, modeled the carrying capacities of 52 countries by analyzing their water trade network. Some of these countries, including Australia, Brazil, and the U.S., are “water-rich,” meaning they can produce their own water and the food that depends on it. Other countries, including Mexico and most of Europe, are “water poor”: They rely on imports.
The researchers considered two possible scenarios. First, they assumed that as water-rich populations neared their limit, they would stop exporting and instead hoard their water resources. In this situation, according to the team’s calculations, water-dependent populations would peak around 2030. However, if countries worked together, continuing to trade as supplies decreased, the entire network could sustain itself until as late as 2060.
Maybe Malthus’ bleak prophecy, more than a century overdue, will finally come to pass. But maybe not. Maybe we’ll find an economical way to desalinate seawater. Maybe we’ll figure out how to grow all of our food in vertical farms. Maybe we’ll start to colonize other planets. For the next generation of demographers to come up with a new, higher limit, though, we’ll need to do more than create: We’ll need to cooperate.

Adam Kucharski is a lecturer in mathematical modeling at the London School of Hygiene & Tropical Medicine. His first book The Perfect Bet: How Science and Math Are Taking the Luck Out of Gambling will be published in the spring of 2016.
























