The adventures of the classic science-fiction novel Flatland by Edwin Abbott have sprung to life. The novel is narrated by a two-dimensional creature who calls himself “A Square,” who learns he has been embedded in a three-dimensional realm called Spaceland without knowing it. Like Mr. Square, physicists over the past century have begun to consider whether our world may be just a slice of a four- or even 10-dimensional expanse. If we could ascend into that higher domain, we would free ourselves from the straitjacket of ordinary space. We could bend our arm through an extra dimension to reach into a locked safe, or see the insides of a human body laid out before us. And we might finally apprehend the deep unity of nature.
But in recent years the dimensional saga has taken a curious twist: Space may not have more dimensions than we perceive around us, but fewer.
The dimensional constriction is wrapped around a problem with gravity, one of the four basic forces of nature. The gravitational attraction between two bodies gets stronger as the bodies get closer. That’s also true for other forces, like the electromagnetic and the weak force. But unlike those forces, gravity undergoes an additional strengthening on small scales. Its attractive force depends on the bodies’ masses or, equivalently, energy, and the uncertainty principle of quantum physics leads to a minimum in the amount of that energy. When the bodies are close enough to each other, that minimum begins to increase in inverse proportion to distance, causing them to attract with redoubled intensity. The other forces of nature also undergo a quantum strengthening or weakening, but to a much lesser degree. As a result, gravity, which is a pushover on everyday scales, catches up with the other forces and becomes their equal at a sub-sub-subatomic distance known as the Planck scale (around a few trillionths of a trillionth of a trillionth of a meter).
With gravity no longer increasing in strength, nothing distinguishes one scale from another. Everything looks the same.
In fact, standard gravity theory predicts that gravity becomes so strong on this scale that matter will collapse into black holes. And because gravity reflects the shape of spacetime, its limitless intensification suggests that the spacetime continuum gets ripped to shreds, so that the featureless expanse of space we experience in everyday life cannot be a fundamental feature of reality. Either some other structure must replace it, or something must save gravity from blowing up at small scales, preserving the fundamental status of spacetime—or both. Either way, the standard theory must be incomplete.
Fathoming the microscopic structure of spacetime is the problem of quantum gravity, which has flummoxed physicists from Einstein on. Put three theorists in a room and you will hear four ideas for what it could be: A chessboard-like arena of discrete cells, a foam of fluctuating geometry, a condensate of vibrating strings, a fabric of interwoven loops, and more.
Surprisingly, though, theorists are now finding that many of these diverse possibilities have a common feature: Space on its finest scales sheds all of its dimensions but one, taming gravity in the process. In fact, a one-dimensional space is the only venue in which the force of gravity doesn’t explode as distance shrinks.
Whether the dimensional shrinkage saves spacetime as a fundamental feature of nature, or is a prelude to its final disappearance, remains unclear. Whatever the case may be, though, “two dimensions [one space and one time] seems to be the natural dimensions where gravity wants to live,” in the words of theoretical physicist Frank Saueressig of Radboud University in the Netherlands.1
In the language of Flatland, we may all be living not in Spaceland, but in Lineland.
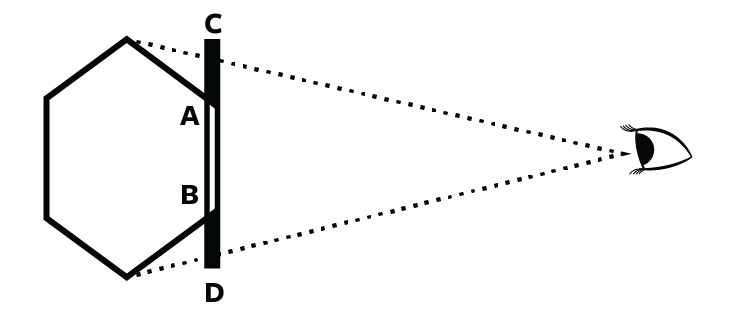
As mysterious as the dimensionality of space might seem, it has a very tangible meaning: It determines how the size of objects, the pace of events, and the strength of forces change when things get bigger or smaller. In ordinary 3-D space, if you double the radius of a sphere, its volume will increase eightfold. In 4-D space, it would go up 16-fold; in 2-D, only fourfold.
So, if you didn’t know how many dimensions space had, you could infer it from how volumes scale. And if you noticed that the scaling relation didn’t stay fixed—if you kept doubling the radius of the sphere and its volume no longer increased by a factor of eight—you’d discern that the dimensionality of space was varying.
That is what many physicists suspect is happening to gravity.
What got them thinking along these lines was a series of computer simulations of the Planck-scale shape of spacetime in the mid 2000s. Renate Loll, at Radboud, and her colleagues devised an algorithm called causal dynamical triangulations to imbue their simulated spacetimes with quantum attributes. They were able to show that space on observable scales should have three dimensions, just as we experience it. But if the strength of gravity were to vary, space could undergo a transition to either a treelike structure with fewer dimensions, or a crumpled wad with more, almost as if space were freezing or boiling.
And even when space seems reassuringly 3-D, it belies that appearance. The researchers imagined setting out on a meandering stroll, taking each step in a random direction, much as a gas molecule will do while caroming around a volume. In 3-D space, if you double the length of your journey, your chance of returning to your starting point should drop by the square root of eight. Yet the simulations found a slower decline near the Planck scale, as if there were less space to get lost in. That’s a telltale sign of fewer dimensions.
By the volume measure, space is 3-D, but by the behavior of random motion, it is 1-D, or even a fractional dimension. This discrepancy is a signal not only that space gets less roomy, but that its very nature changes as gravity begins to show its quantum aspects. “When you don’t have a normal manifold, there are typically many different definitions of ‘dimension,’ ” says Steve Carlip at the University of California, Davis.
The spacetime continuum gets ripped to shreds, so that the featureless expanse of space we experience in everyday life cannot be a fundamental feature of reality.
Like computer simulations in any domain of science, causal dynamical triangulations are a black box: They take equations as input and generate numbers as output, but don’t tell you what is going on and why. “It’s still a mystery, what does it actually mean,” Loll says. So far, the theory that comes closest to explaining these dimensional gymnastics is known as asymptotic safety, a dark-horse candidate for quantum gravity that dates to the late 1970s. It supposes that gravity has a kind of built-in governor, rendering it “safe.” Features of gravity that we never see in daily life kick in near the Planck scale, so that the force reaches some finite maximum strength instead of intensifying without limit. Asymptotic safety appeals to many particle physicists because it implies gravity is just like the forces that govern atomic nuclei, which are known to wimp out at short distances.
According to asymptotic safety, space loses dimensions not because it is flattened like a crushed soda can, but because quantum effects cause it to fluctuate frenetically, altering the usual rules by which particles navigate the world. For example, a randomly caroming particle might retain some memory of its path and avoid where it has already been—like the ’70s-era video game Snake, in which you steer a moving dot while trying not to run into your own path. Saueressig says that because of this constraint on its motion, the particle might have a higher probability of returning to its starting point, producing the effect of moving through fewer dimensions.
As if zapping a dimension or two weren’t radical enough, asymptotic safety also entails an even more profound transformation of space. If gravity plateaus on small scales, never becoming strong enough to give rise to Planck-scale black holes, then the spacetime continuum doesn’t get shredded, as standard theory predicts. Instead, it remains truly continuous: You can zoom in without limit. But if you do zoom in, you will quickly find yourself disoriented. With gravity (and possibly the other forces of nature as well) no longer increasing in strength, nothing distinguishes one scale from another. Everything looks the same. Each part resembles the whole. This is the very definition of a fractal structure.
Martin Reuter, the doyen of asymptotic safety, at the University of Mainz in Germany, compares the universe at this level to a turbulent fluid: eddies within eddies within eddies. Distance ceases to have a fixed meaning, since the length of the path between any two points will depend on the zoom level, just as the coastline of Great Britain gets longer as you add up ever more of its wiggles.
One-dimensional space certainly seems to save gravity from itself. But that merit is not enough, on its own, to convince physicists that space really does shed dimensions at small scales. The first test of any theory is its internal consistency. Proponents of asymptotic safety, as well as other approaches that suggest a loss of dimensions, openly admit that they have yet to demonstrate this.
In fact, some critics think asymptotic safety can’t work, because it falls down on the physics of black holes. The internal complexity of these cosmic sinkholes scales up with their exterior surface area. But in any theory formulated in a continuum, including asymptotic safety, complexity should scale up with the interior volume. Proponents counter that these scaling rules would change if the number of spatial dimensions did, perhaps ensuring that everything works out.
And even if asymptotic gravity is not the ultimate theory, it might still be a useful stepping stone to a putative theory in which space emerges from an underlying spaceless level. “Between ‘no spacetime’ and ‘usual spacetime,’ there may well be ‘weird spacetime,’ ” says Daniele Oriti of the Max Planck Institute for Gravitational Physics in Potsdam, Germany.
Laboratory experiments aren’t likely to settle this issue anytime soon—or, indeed, much of anything when it comes to quantum gravity, since the Planck scale is so much smaller than what modern instruments can probe. Cosmological observations are a better bet. Reuter points out that the early universe did look scale-invariant: Density variations of every size had the same magnitude. This supports the asymptotic-safety theory, and a spacetime that is a fundamental feature of nature. But other theories offer alternative explanations for the scale-invariance.
Even if all the theories suggesting dimensional disappearance are proved wrong, they might, in hazy ways, be picking up on a deep feature of quantum gravity. “This is part of the reason it’s so interesting,” Carlip says. “It may reveal something deep about quantum gravity that these very different approaches all have in common. But we don’t know what that is.”
In the preface to the 1884 edition of Flatland, Abbott decries, in the voice of his character A Square, how we are “all alike the Slaves of our respective Dimensional prejudices.” Today, physicists are learning to discard their own dimensional prejudices. After all, as Mr. Square writes, “one touch of Nature makes all worlds akin.”
George Musser is a writer on physics and cosmology and the author of The Complete Idiot’s Guide to String Theory and Spooky Action at a Distance (forthcoming from Farrar, Straus and Giroux). He was a senior editor at Scientific American for 14 years and has won the American Institute of Physics Science Writing Award, among others.






























