My aim as a theoretical physicist is to unite quantum theory with Einstein’s Theory of General Relativity. While there are a few proposals for this unification, such as string theory and loop quantum gravity, many roadblocks to a complete unification remain.
Einstein’s theory tells us the gravitational force is a direct manifestation of space and time bending. The sun bends the fabric of space, much like a sleeping person bends a mattress. Planetary orbits, including Earth’s, are motion along the contours of the bent space created by the sun. This theory provides some critical insights into the nature of light.
As I gazed at the drawing, I could feel the artists challenging me to reconsider the nature of light.
Quantum mechanics, however, says many weird things about physical reality. For instance, our experience is to occupy a single region of space. But when a quantum particle moves through space, it considers all paths at the same time, as if many copies of the particle coexisted at the same time.
For years I have been stuck in my research, unable to make the progress I envisioned early in my career. Notably, quantum mechanics carefully takes the role of the observer into the structure of the theory. But it has proven incredibly difficult to include the role of the observer in a quantum spacetime.
Late last summer, I had the most unexpected breakthrough. Beth Jacobs, a member of the New York Academy of Sciences’ Board of Governors, invited me and some friends to her New York City apartment to meet the Oakes twins, artists who have gained attention in recent years for their drawings as well as the innovative technique and inventions they deploy to create them. An Oakes work, Irwin Gardens at the Getty in Winter (2011), an intricate drawing of the famous gardens designed by Robert Irwin at The Getty Museum in Los Angeles, was displayed on the balcony of Jacobs’ apartment overlooking Central Park, with the backdrop of the New York City skyline lit with a warm orange sky moments before sunset.

As I gazed at the drawing, I could feel the artists challenging me to reconsider the nature of light. I began to realize I should consider not only the physics of light, but also how light information is perceived by observers, when theorizing and conceiving new principles to unify quantum mechanics and general relativity. I was already on that path by investigating the perception of time and quantum uncertainty in the scratch-film works of Sam Heydt, a photographer and multimedia artist, whose works evoke the bending of temporal events. My mind was ripe for new inspiration and here were the Oakes twins to provide it.
Ryan and Trevor Oakes, 35, have been exploring the impact and intersection of visual perception and the physics of light since they were kids. After attending The Cooper Union for the Advancement of Science and Art in New York City, and years of experimentation and inventing new techniques, the twins exploited the notion that light information is better described when originating from a spherical surface.
Writer Lawrence Weschler summarizes their process well. In 2014, Weschler curated a retrospective of the twins’ work at the National Museum of Mathematics in New York. He wrote that the brothers have “developed one of the most intriguing breakthroughs in the depiction of physical reality since the Renaissance: They have come up with a method for tracing camera-obscura-exact renderings of the world before them onto a concave grid with no other optical equipment (no lenses, no pinholes) except their own unaided eyes.”
After my introduction to the Oakes brothers, I began to explore their work in depth. I saw that behind its magic is a practice of experimentation, intuition, approximation, and technique that parallels that of top-flight physicists. The twins have awakened me to the intricate ways in which art and science inform each other and to the vast, uncharted terrain for conversations and collaborations between artists and scientists. Among the threads woven into the fabric of both art and science is the way artists and scientists develop and exploit technique to reveal hidden reality, to focus on a secret staring us right in the face.
In addition to the unique, concave canvas the twins use to create and display their drawings, their use of a circular basis for pixilating the details of their drawings intrigued me. It reminded me of the technique employed by Van Gogh in his later works to create, in the colors’ reflection of light, the effect of almost an extra dimension of textural depth. The shades can be perceived as three-dimensional information from a two-dimensional canvas. Likewise I was intrigued by the twins’ use of embedded circles, and the technique giving expression to that choice.

The Oakes brothers also got me thinking about the tradition of “thought experiments,” which Einstein used as a method for elucidation and expression. From years of experimentation with visual perception, the brothers have teased out an understanding of the physical form of visual information.
At any moment, they explain in an email, “Our eyes are only able to gather the light rays that happen to be aimed straight toward them. Collectively, any group of light rays that happen to converge onto one’s pupil are, altogether, fanned out radially from the pupil, with each light ray traveling perpendicular to the surface of an implied sphere. The surrounding objects of the world may be irregular and varied, but perceptually we live neatly at the center of a sphere of incoming photons that carry information about the irregular surround to our eyes.”
To capture this geometric shape of perception, the brothers create their artworks on a spherically concave surface, instead of the traditional flat picture plane. The use of a concave surface to render a scene, as in The Getty, Trevor Oakes says, “is in harmony with the shape of light rays and makes more sense than a flat picture plane.”
But what does the physics of light say about the Oakes brothers’ discovery and technique? Quite a lot, actually. Our story begins with James Clerk Maxwell’s discovery in the 1860s that electricity and magnetism are unified into electromagnetism and are interdependent phenomena. This discovery means that light is a wave of undulating electric and magnetic fields—electromagnetic waves—moving through space at the speed of light.
The Oakes brothers have awakened me to the intricate ways in which art and science inform each other.
Equipped with this knowledge, a young Einstein cooked up the following thought experiment: “If I pursue a beam of light … I should observe such a beam of light as an electromagnetic [wave] at rest although spatially oscillating. There seems to be no such thing.” The technique pivoted on intuition, creativity, and a base understanding of physics.
Einstein tried to imagine what the world would look like if he managed to catch up to a wave of light and surf on it. He reasoned that he would perceive the electromagnetic wave as being at rest. This situation, Einstein realized, exposed a paradox: In Maxwell’s theory of light, there was never a situation in which a wave of light could be at rest. This paradox and its resolution were at the heart of the discovery of relativity theory—that the speed of light is always a fixed value even if you managed to get very close to catching up to it. How can this be possible?
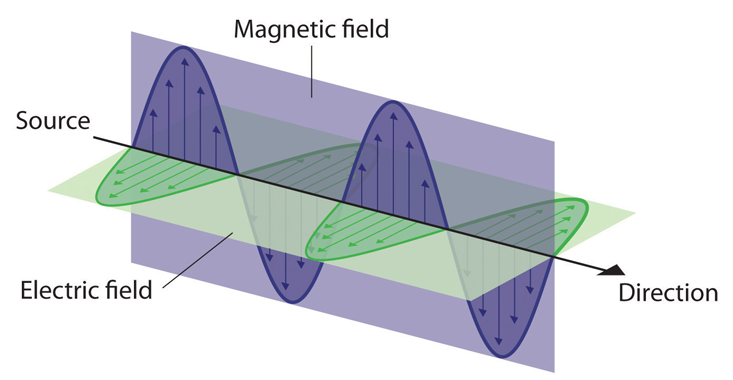
Einstein realized that if you are traveling really fast, your watch can tick slower compared to someone not moving at all. This seems weird, but it is true. And it means that even when you move nearly as fast as light, because time is perceived to be slower and the speed at which objects are moving depends on the distance covered in a given time interval, light will nevertheless appear to be moving at the same speed as it does to the person not moving at all.
At the heart of this relativity is the realization that as a result of this resolution of the paradox, space and time must be unified in a four-dimensional space-time continuum. As a result, time and space are no longer absolute, but depend on how fast one is moving. Moreover, light does not exist in space and time separately; light is not simply a wave distributed in space that evolves in time. Like space and time, light also becomes a four-dimensional entity. In this view Einstein realized that the electric and magnetic fields were three-dimensional projections of a four-dimensional light wave; much the same way that your two-dimensional shadow cast by sunlight is a projection of your three-dimensional self.
It is through this realization that we can understand the twins’ use of spheres. But we need one more analogy.
Let’s imagine dropping stones on a pond. Each time we drop a stone we see a circular wave pattern emanate away from the point of impact. The surface of the water is two-dimensional and the resulting waves will move outward as circular rings. A similar thing happens if a disturbance occurs below the surface where the environment is 3-D. In that case the waves would be a two-dimensional surface that would move outward like an expanding bubble.
What is mind-bending is they arrived at this insight in the same way a theoretical physicist unearths new truths.
It turns out that this physical description carries over for light. In this case the stone hitting the water is analogous to a source of light moving toward your eyes. As the twins correctly found, light information will leave the source—each point of the canvas—as a spherical light wave. But why would light want to take the form of a spherical wave when it moves through space? This is where the four-dimensional spacetime description of light is essential. And this is where I became fascinated with the intuition behind the twins’ representation of concavity and spheres as a technique of experimenting with their own perception and theoretical knowledge of the physics of light.
To understand why light moves away from its source as an expanding spherical wave front, we need Einstein’s theory of special relativity. Not only does light move through space and time, but Einstein taught us that the structure of space and time informs light how to move. Much like the wind propels a sailboat’s motion, light is sailing the winds of spacetime so to speak. Einstein’s resolution to his paradox about riding a light wave was that space and time had to be merged into four-dimensional spacetime. We no longer exist at a point in three-dimensional space but at a point in four-dimensional spacetime. For example, as you sit reading this article, you exist in a three-dimensional spatial location at a particular point in time. At some later time, you will exist at a different point in four-dimensional spacetime.
This has consequences for light. In the figure below we see that light is no longer a point in space, but rather a cone in spacetime.
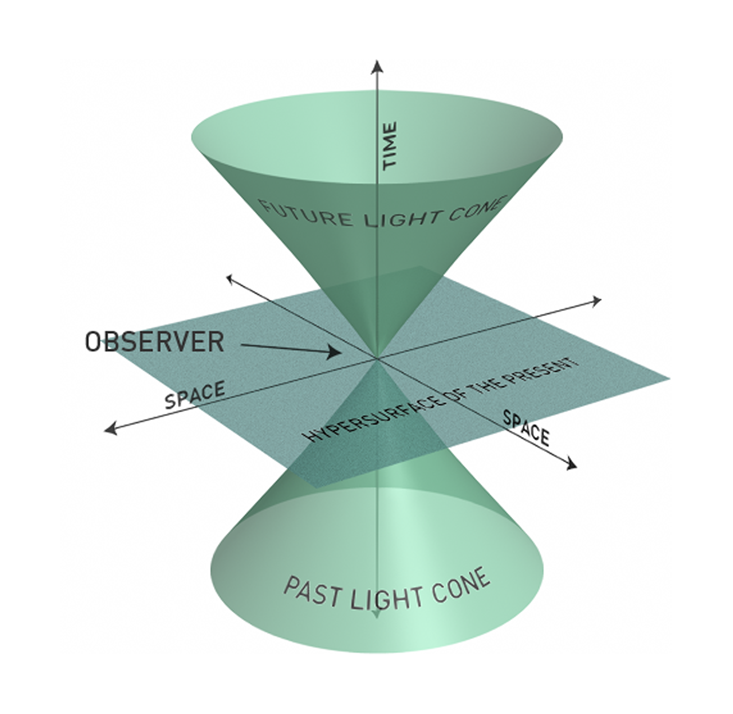
This is the correct picture of light as it is created at a point in spacetime and shows how it moves to other points in spacetime. The light traces out a cone as time develops, toward the future. If we trace a single point in time, we get sequences of moving circular rings. These circles are analogous to the spherical waves that the twins implemented in their work. Now it made complete sense why they pixilated their work Bond Street Terrace with circles.

A ray of light is a manifestation of four-dimensional spacetime. The equation for this light cone is well known: X2 + Y2 + Z2 – c2T2 = 0. This equation is so beautiful that it’s worth saying a few words about it. Realize that the left hand side of the equation depends on three spatial directions (X, Y & Z), time (T), and the speed of light (c). If we were to ignore time, this is the equation for a three-dimensional surface. The inclusion of the time direction makes an equation that describes a light cone as depicted in the figure above. Below is a computer-generated snapshot of the spherical waves tracing out the different points of the light cone emanating from its point of creation. The blue regions represent the time development of the spherical waves.

It is truly astonishing that the twins arrived at an aspect of a most beautiful and earth-shattering idea in physics—the spherical emanation of light—through perception alone. What is even more mind-bending is that they arrived at this insight by developing their own techniques through intuition, experimentation, and approximations—the same way that a good theoretical physicist may want to unearth new truths.
The twins’ work gave me insight into the unification between quantum mechanics and gravity by reminding me that spacetime and light are intimately connected, and so are observers. A precise understanding of how to incorporate observers, conscious or not, in quantum gravity is still missing. Yet the twins reminded me to take this issue seriously in my research. When I see artists like the Oakes brothers arriving at and employing physical insights based on their own experimentation and intuitions, I gain a confidence that a continued conversation with artists could very well be that extra jolt that takes me into unchartered conceptual territories, and perhaps a solution that I hope will be as beautiful as the twins’ drawings.
Stephon Alexander is a professor of physics at Brown University specializing in theoretical cosmology and quantum gravity. He is a specialist in the field of string cosmology, where the physics of superstrings are applied to address longstanding questions in cosmology. He is also a jazz saxophonist and the author of The Jazz of Physics.






























